
- •П.1. Поняття функціональної залежності, числова функція.
- •Лекційний матеріал до теми.
- •1.Історія виникнення поняття функції.
- •3. Числова функція. Область визначення функції.
- •4. Способи задання функції
- •П.2. Неперервність функцій. Типи розривів числових функцій
- •Лекційний матеріал до теми.
- •1. Неперервність функцій.
- •2. Типи розривів числових функцій
- •Тема 2. Степенева, показникова і логарифмічна функції. П.1. Логарифмування та потенціювання виразів
- •Лекційний матеріал до теми.
- •Логарифмування виразів
- •Розв'язання
- •2.Потенціювання виразів.
- •Розв'язання
- •Тема 3 . Тригонометричні функції. П.1. Формули половинного аргументу, формули потрійного аргументу
- •Лекційний матеріал до теми.
- •1. Формули половинного аргументу
- •2.Формули потрійного аргументу
- •Тема 4 . Рівняння, нерівності та їхні системи. П.1.Розв’язування задач, що приводять до розв’язування рівнянь та систем рівнянь
- •Лекційний матеріал до теми.
- •Хімічні задачі
- •Задачі на рух.
- •Задачі, в яких кількість невідомих більша за кількість рівнянь системи.
- •Тема 5 . Вектори і координати. П.1. Вектори в просторі. Дії над векторами. Розклад вектора на складові
- •Лекційний матеріал до теми.
- •1.Вектори в просторі. Дії над векторами.
- •Розклад вектора на складові.
- •Тема 6 . Систематизація та узагальнення фактів і методів планіметрії.
- •Лекційний матеріал до теми.
- •1.Формула площі трикутника за двома сторонами і кутом між ними.
- •2. Формула площі трикутника за стороною і опущеною до неї висотою.
- •3.Формула Герона
- •4.Формули площ трикутника з використанням радіусів вписаного та описаного навколо трикутника кола
- •Тема 7 . Паралельність та перпендикулярність прямих і площин у просторі.
- •1.Взаємне розміщення двох прямих у просторі
- •Лекційний матеріал до теми.
- •Взаємне розміщення двох прямих у просторі
- •2.Теорема про існування і єдиність прямої, яка проходить через дану точку і паралельна даній прямій
- •Ознака паралельності прямих
- •Доведення
- •П.2. Теореми про паралельні площини
- •Лекційний матеріал до теми
- •2. Теорема про відрізки паралельних прямих, які містяться між двома паралельними площинами
- •Доведення
- •Розв'язання
- •П.3. Ознака перпендикулярності двох прямих в просторі
- •Лекційний матеріал до теми
- •Тема 8. Похідна та її застосування.
- •Лекційний матеріал до теми
- •П.2. Дослідження функції на екстремум за допомогою другої похідної
- •Лекційний матеріал до теми
- •Тема 9. Інтеграл та його застосування п.1. Правила знаходження первісної. Фізичні застосуванні первісної функції
- •Лекційний матеріал до теми
- •Правила знаходження первісних
- •Розв'язання
- •Розв'язання
- •2.Застосування первісної для відновлення рівняння руху точки
- •Розв'язання
- •П.2. Поняття криволінійної трапеції
- •Лекційний матеріал до теми
- •П.3. Застосування визначеного інтегралу в економіці, техніці, фізиці.
- •Лекційний матеріал до теми
- •П.4. Рівняння гармонійних коливань
- •Лекційний матеріал до теми
- •Тема 10. Многогранники. Об’єми та площі поверхонь многогранників п.1. Вимірювання відстаней у просторі. Вимірювання кутів у просторі. Двогранний кут
- •Лекційний матеріал до теми
- •1. Вимірювання відстаней у просторі.
- •Задача з точки м опустити перпендикуляр на пряму ав
- •2 . Поняття двогранного кута та його елементів, лінійного кута двогранного кута
- •Задача 3*
- •Задача 4*
- •Тема 11. Тіла обертання. Об’єми та площі поверхонь тіл обертання
- •Лекційний матеріал до теми
- •1. Комбінації многогранників
- •Задача1
- •Розв'язання
- •2.Комбінації многогранників і циліндра
- •3.Комбінації многогранників і конуса
- •4.Комбінації многогранників і кулі
- •5. Куля і конус
- •6. Куля і циліндр
- •7. Конус і циліндр
- •Тема 12. Елементи теорії ймовірностей і математичної статистики
- •Лекційний матеріал до теми
- •Тема 13. Повторення, узагальнення та систематизація навчального матеріалу, розв’язування задач.
- •Лекційний матеріал до теми
- •4. Геометрична прогресія.
- •Література
4. Геометрична прогресія.
Геометричною прогресією називається послідовність відмінних від нуля чисел, кожний член якої, починаючи з другого, дорівнює попередньому, помноженому на те саме число (знаменник геометричної прогресії). |
Приклад. 3; 9; 27; 81; 243; ... — геометрична прогресія, бо а2 = а1 ∙ 3; а3 = а2 ∙ 3; а4 = а3 ∙ 3; ... . (3 — знаменник цієї прогресії). |
Рекурентна формула геометричної прогресії |
Якщо (bп) — геометрична прогресія, то bn+1 = bnq, де bп — п-й член; q — знаменник геометричної прогресії.
З
рекурентної формули випливає:
|
Властивості геометричної прогресії: |
а) для
кожного члена геометричної прогресії,
починаючи з другого:
|
б) якщо (bп) — скінченна геометрична прогресія, то b1 ∙ bn = b2 ∙ bn-1 = b3 ∙ bn-2 = const (b1 і bn — крайні члени цієї прогресії). |
5. Формула п-го члена геометричної прогресії |
Якщо (bn) — геометрична прогресія, то bn=blqn-1, де b1 — перший член геометричної прогресії; q — знаменник геометричної прогресії. |
Приклад
1.
Знайдемо шостий член геометричної
прогресії (b1):
Розв'язання
b1
=
;
q =
Відповідь: 625. |
Приклад 2. Знайдемо перший член геометричної прогресії (bn), якщо b7 = 32; q = -2. Розв'язання
b7
= b1
∙ q6
Відповідь: . |
Приклад 3. Знайдемо знаменник геометричної прогресії (bn), у якої b7 = -12, b9 = -108. Розв'язання
b9
= b1
∙ q8;
b7
=
b1∙
q6
Відповідь: 3 або -3. |
6.Формули суми перших п членів геометричної прогресії |
Якщо (bn) — геометрична прогресія, q — її знаменник, a Sn — сума перших n її членів, то: (1)
або
! Зауваження: якщо q = 1, то Sn = b1 ∙ n (b1 = b2 =... = bn). |
Приклад 1. Знайдемо суму перших восьми членів геометричної прогресії (bn): 3; -6; 12; ... . Розв'язання
Маємо
b1 = 3, q =
S8 =
Відповідь: -255. |
Приклад 2. Знайдемо перший член геометричної прогресії (bп), якщо її четвертий член утричі більший за третій, а сума перших п'яти членів дорівнює -12,1. Розв'язання
Оскільки
b4 = 3b3, то q = 3. За умовою S5 = -12,l, тому,
оскільки
Відповідь: -0,1. |
7.Нескінченна геометрична прогресія, у якої | q | < 1 |
Приклади:
а) 1;
;
б) 3;
в) 100;
10; 1;
г) 32;
0,32; 0,0032; ... q =
|
Якщо (bn) — нескінченна геометрична прогресія, у якої | q | < 1, то сума всіх її членів S обчислюється за формулою
|
Приклад 1. Знайдемо суму нескінченної геометричної прогресії (bn): 6; -2; ... . Розв'язання За умовою b1 = 6; b2 = -2, отже, q = = . Маємо геометричну прогресію, у якої | q | < 1. За формулою знаходимо:
Відповідь; 4,5. |
Приклад 2. Запишемо число 0,(7) у вигляді звичайного дробу. Розв'язання Запис 0,(7) означає нескінченний періодичний дріб 0,7777....
Його
можна подати як нескінченну суму
Доданки цієї суми є членами нескінченної геометричної прогресії, у якої b1 = , q = : = , | q | < 1. Тоді ця сума дорівнює:
Відповідь: . |
№1. Знайдіть перші чотири члени арифметичної прогресії (аn), якщо а1 = 1,2, d = -0,l.
№2.Знайдіть різницю і сотий член арифметичної прогресії (ап): 2,7; 3,1; 3,5; ... №3.Між числами -4 і 5 вставте п'ять таких чисел, щоб вони разом із даними числами утворювали арифметичну прогресію.
№4.Дана арифметична прогресія: 2; 1,8; 1,6; ... . Знайдіть її найбільший від'ємний член.
№5. Знайдіть суму:
а) перших шістнадцяти членів арифметичної прогресії, якщо її перший і шістнадцятий члени відповідно дорівнюють 3 і -5;
б) перших шістнадцяти членів арифметичної прогресії, якщо її перший член дорівнює 6, а різниця 3;
в) перших сорока семи членів арифметичної прогресії, яка задана формулою загального члена ап = 3п – 1;
г) членів арифметичної прогресії з 6-го по 23-й включно, якщо перший член дорівнює 28, а п'ятий дорівнює 16.
№6. Знайдіть суму:
а) перших п'яти членів геометричної прогресії (bп), якщо b1 = 8, q = ;
б)
перших шести членів геометричної
прогресії (bп):
 ;
;
 ;
;
… ;
;
;
… ;
в) перших семи членів геометричної прогресії (bп), якщо вона задана формулою загального члена bп = 3 ∙ 2n+1;
г) перших п'яти членів геометричної прогресії (bп), якщо сума другого і третього її членів дорівнює -12, а різниця четвертого і другого членів дорівнює 48.


 —характеристична
властивість;
—характеристична
властивість; ;
1; 5; ... .
;
1; 5; ... . = 5; b6
= b1
∙ q5 =
∙ 55 = 54 = 625.
= 5; b6
= b1
∙ q5 =
∙ 55 = 54 = 625.
 b1 =
b1 =
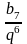 =
=
 =
.
=
.
 = q2;
q2
=
= q2;
q2
=
 = 9, тоді q = 3 або q = -3.
= 9, тоді q = 3 або q = -3.
 (2)
(2) = -2, тоді за формулою (2):
= -2, тоді за формулою (2):
 =
=
 =
=
 =
-255.
=
-255.
 ,
тобто
,
тобто
 ;
-12,1 = 121b1; b1 = -0,1.
;
-12,1 = 121b1; b1 = -0,1. ;
;
 ;
... q =
,
| q | < 1;
;
... q =
,
| q | < 1; ;
;
 ;
... q =
;
... q =
 ,
| q | < 1;
,
| q | < 1; ;
... q =
,
| q |< 1;
;
... q =
,
| q |< 1; ,
| q | < 1.
,
| q | < 1. .
. +
+
 +
+
 + … .
+ … .
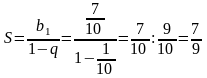 . Тому
0,(7) =
. Тому
0,(7) =
 .
.