
- •П.1. Поняття функціональної залежності, числова функція.
- •Лекційний матеріал до теми.
- •1.Історія виникнення поняття функції.
- •3. Числова функція. Область визначення функції.
- •4. Способи задання функції
- •П.2. Неперервність функцій. Типи розривів числових функцій
- •Лекційний матеріал до теми.
- •1. Неперервність функцій.
- •2. Типи розривів числових функцій
- •Тема 2. Степенева, показникова і логарифмічна функції. П.1. Логарифмування та потенціювання виразів
- •Лекційний матеріал до теми.
- •Логарифмування виразів
- •Розв'язання
- •2.Потенціювання виразів.
- •Розв'язання
- •Тема 3 . Тригонометричні функції. П.1. Формули половинного аргументу, формули потрійного аргументу
- •Лекційний матеріал до теми.
- •1. Формули половинного аргументу
- •2.Формули потрійного аргументу
- •Тема 4 . Рівняння, нерівності та їхні системи. П.1.Розв’язування задач, що приводять до розв’язування рівнянь та систем рівнянь
- •Лекційний матеріал до теми.
- •Хімічні задачі
- •Задачі на рух.
- •Задачі, в яких кількість невідомих більша за кількість рівнянь системи.
- •Тема 5 . Вектори і координати. П.1. Вектори в просторі. Дії над векторами. Розклад вектора на складові
- •Лекційний матеріал до теми.
- •1.Вектори в просторі. Дії над векторами.
- •Розклад вектора на складові.
- •Тема 6 . Систематизація та узагальнення фактів і методів планіметрії.
- •Лекційний матеріал до теми.
- •1.Формула площі трикутника за двома сторонами і кутом між ними.
- •2. Формула площі трикутника за стороною і опущеною до неї висотою.
- •3.Формула Герона
- •4.Формули площ трикутника з використанням радіусів вписаного та описаного навколо трикутника кола
- •Тема 7 . Паралельність та перпендикулярність прямих і площин у просторі.
- •1.Взаємне розміщення двох прямих у просторі
- •Лекційний матеріал до теми.
- •Взаємне розміщення двох прямих у просторі
- •2.Теорема про існування і єдиність прямої, яка проходить через дану точку і паралельна даній прямій
- •Ознака паралельності прямих
- •Доведення
- •П.2. Теореми про паралельні площини
- •Лекційний матеріал до теми
- •2. Теорема про відрізки паралельних прямих, які містяться між двома паралельними площинами
- •Доведення
- •Розв'язання
- •П.3. Ознака перпендикулярності двох прямих в просторі
- •Лекційний матеріал до теми
- •Тема 8. Похідна та її застосування.
- •Лекційний матеріал до теми
- •П.2. Дослідження функції на екстремум за допомогою другої похідної
- •Лекційний матеріал до теми
- •Тема 9. Інтеграл та його застосування п.1. Правила знаходження первісної. Фізичні застосуванні первісної функції
- •Лекційний матеріал до теми
- •Правила знаходження первісних
- •Розв'язання
- •Розв'язання
- •2.Застосування первісної для відновлення рівняння руху точки
- •Розв'язання
- •П.2. Поняття криволінійної трапеції
- •Лекційний матеріал до теми
- •П.3. Застосування визначеного інтегралу в економіці, техніці, фізиці.
- •Лекційний матеріал до теми
- •П.4. Рівняння гармонійних коливань
- •Лекційний матеріал до теми
- •Тема 10. Многогранники. Об’єми та площі поверхонь многогранників п.1. Вимірювання відстаней у просторі. Вимірювання кутів у просторі. Двогранний кут
- •Лекційний матеріал до теми
- •1. Вимірювання відстаней у просторі.
- •Задача з точки м опустити перпендикуляр на пряму ав
- •2 . Поняття двогранного кута та його елементів, лінійного кута двогранного кута
- •Задача 3*
- •Задача 4*
- •Тема 11. Тіла обертання. Об’єми та площі поверхонь тіл обертання
- •Лекційний матеріал до теми
- •1. Комбінації многогранників
- •Задача1
- •Розв'язання
- •2.Комбінації многогранників і циліндра
- •3.Комбінації многогранників і конуса
- •4.Комбінації многогранників і кулі
- •5. Куля і конус
- •6. Куля і циліндр
- •7. Конус і циліндр
- •Тема 12. Елементи теорії ймовірностей і математичної статистики
- •Лекційний матеріал до теми
- •Тема 13. Повторення, узагальнення та систематизація навчального матеріалу, розв’язування задач.
- •Лекційний матеріал до теми
- •4. Геометрична прогресія.
- •Література
П.2. Неперервність функцій. Типи розривів числових функцій
Література:
1. М.І.Шкіль. Алгебра і початки аналізу 10-11кл.
2. Нелін Є. П. Алгебра і початки аналізу: Дворівневий підруч. для 10 кл. загальноосвіт. навч. закладів.— 2-ге вид., виправ. і доп. — Х.: Світ дитинства
3. О.М.Роганін. Плани-конспекти уроків
4. О.С.Істер Алгебра 10 клас Дидактичні матеріали
Методичні вказівки:
Точки, у яких при побудові графіка відриваємо олівець від паперу, називають точками розриву, а функцію – розривною в цій точці.
Многочлен у = а0 + а1х + а2х2 +... + аnxn – неперервна функція в будь-якій точці.
Дробово-раціональна функція
 неперервна в усіх точках числової осі,
крім тих точок, у яких знаменник дорівнює
нулю.
неперервна в усіх точках числової осі,
крім тих точок, у яких знаменник дорівнює
нулю.
Крім того, слід зазначити, що вивчені нами функції
у =
 ,
у
= |х|
є також неперервними в усіх точках
області визначення.
,
у
= |х|
є також неперервними в усіх точках
області визначення.
Студенти повинні вміти:
Доводити неперервність числових функцій, з’ясовувати типи розривів функцій
Питання для самоконтролю:
Яка функція називається неперервною?
Розриви функцій яких видів ви знаєте?
Самостійне вивчення з розробкою конспекту та розв’язуванням задач.
План.
Неперервність функцій.
Типи розривів числових функцій
Форми поточного та підсумкового контролю самостійної роботи:
Поточний:
перевірка конспектів
усне опитування
розв’язування задач.
Підсумковий:
тематична контрольна робота
державна підсумкова атестація
Лекційний матеріал до теми.
1. Неперервність функцій.
Розгляньте графіки функцій, зображених на рис. 1.
Р

 ис.
1
ис.
1
Які із цих графіків можна накреслити, не відриваючи олівця від аркуша паперу?
Точки, у яких при побудові графіка відриваємо олівець від паперу, називають точками розриву, а функцію – розривною в цій точці.
На рис. 1 розривними функціями є функції f2, f3, f4, які мають розрив в точці х = 1.
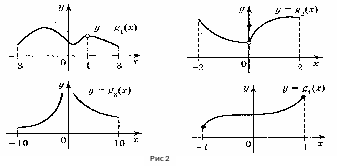
В усіх останніх точках області визначення функцій f2, f3, f4 ці функції не мають розриву. Отже, в інших точках функції f2, f3, f4 неперервні, функція f1 неперервна в кожній точці. Якщо функція у=f(x) неперервна в кожній точці деякого проміжку, то її називають неперервною на даному проміжку. Справедливі такі теореми.
Теорема 1. Якщо функції у = f(x) і у = g(x) є неперервними в точці х , то в цій точці будуть неперервними й функції у = f(x) ± g(x) та у = f(x) – g(x).
Теорема 2.
Якщо функції у
= f(x)
і у = g(x)
є неперервними в точці
хо
і
 ,
то в точці хо,
буде неперервною також і функція
,
то в точці хо,
буде неперервною також і функція
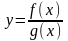 .
.
Висновок:
Многочлен у = а0 + а1х + а2х2 +... + аnxn – неперервна функція в будь-якій точці
 .
.Дробово-раціональна функція неперервна в усіх точках числової осі, крім тих точок, у яких знаменник дорівнює нулю.
Крім того, слід зазначити, що вивчені нами функції
у = , у = |х| є також неперервними в усіх точках області визначення.
Приклад 1. Які із функцій, графіки яких зображено на рисунку 3, неперервні, а які розривні в точці О?
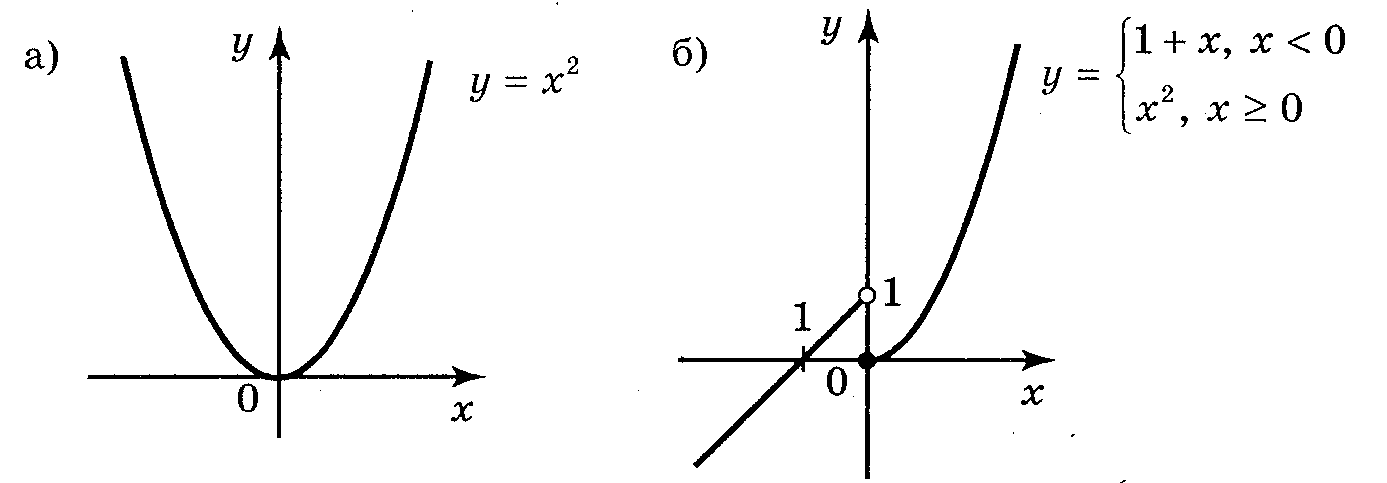
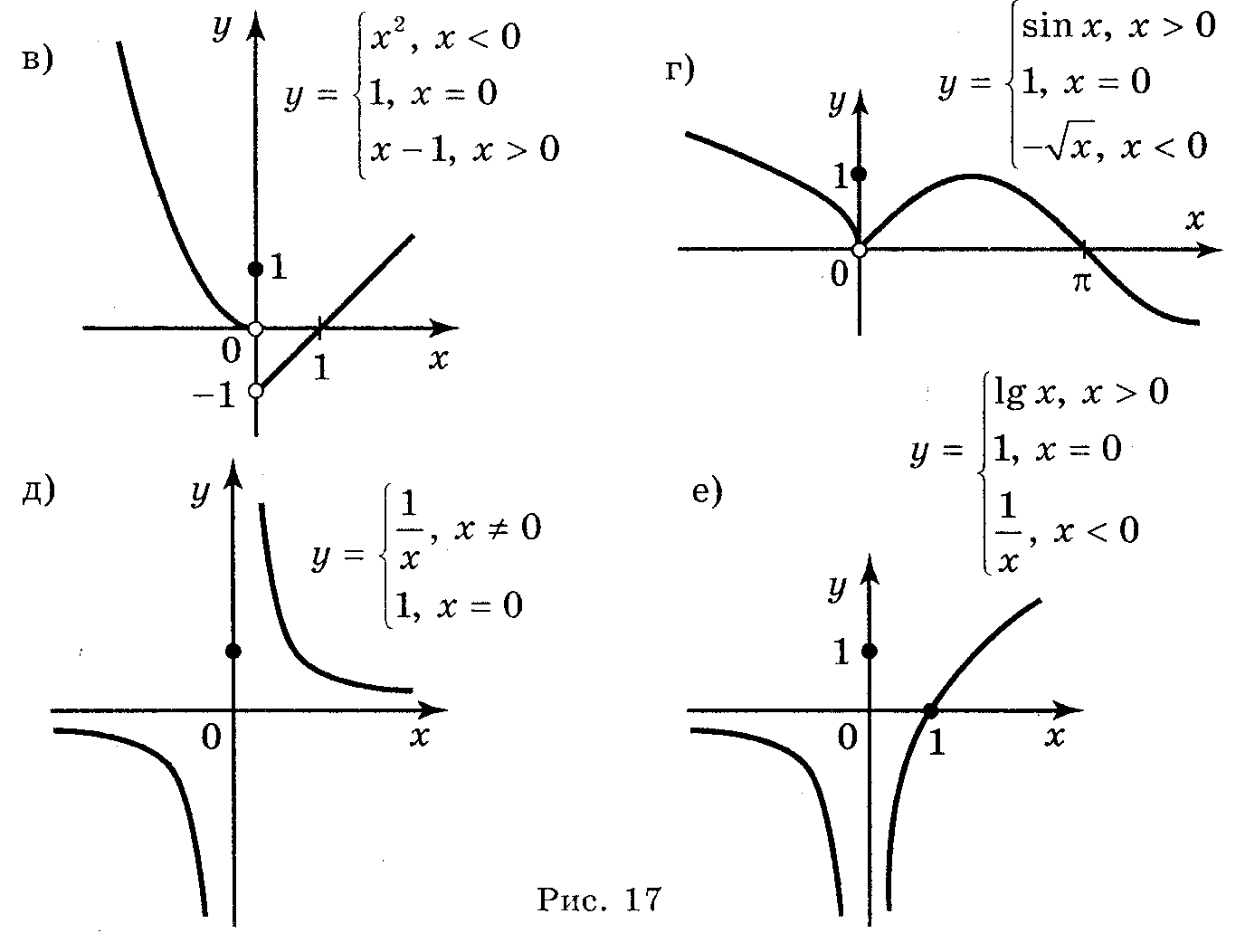
Рис 3
Відповідь: неперервна функція зображена на рис. а; останні функції розривні в точці О.
Приклад 2. Укажіть проміжки неперервності функцій f і g, зображених на рис 4
Відповідь: функція у = f(x) неперервна на проміжках (- ;0), (0; 1), (1;+ ),
функція у = g(x) неперервна на проміжках (- ; 1), (1; + ).

Приклад 3. Побудуйте графік функції у = f(x). Чи міститься в області визначення функції точка, в якій функція не є неперервною?
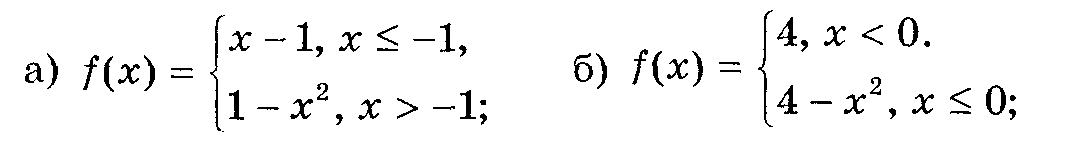
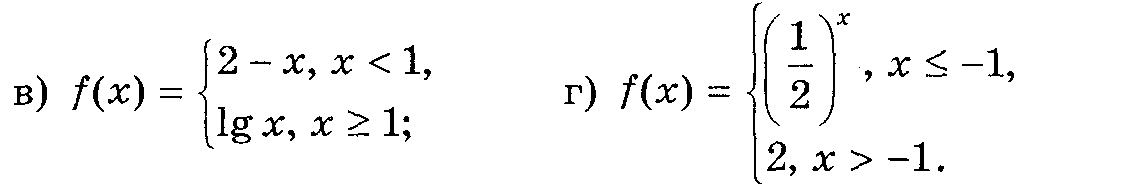
Відповідь: а) Рис. 5, а, функція розривна в точці х = -1;
б) Рис. 5, б, функція неперервна для х R;
в) Рис. 5, е, функція розривна в точці х = 1;
г) Рис. 5, г, функція неперервна для х R.
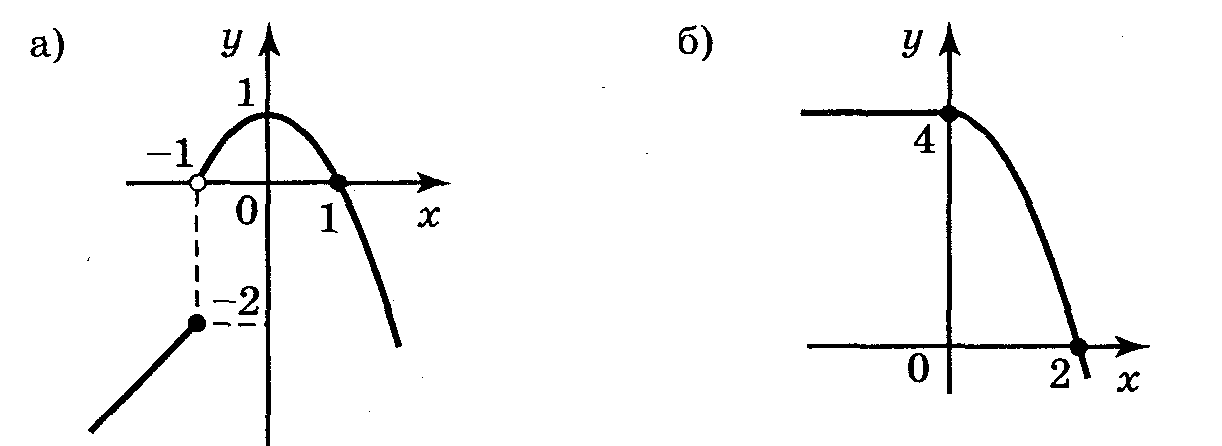
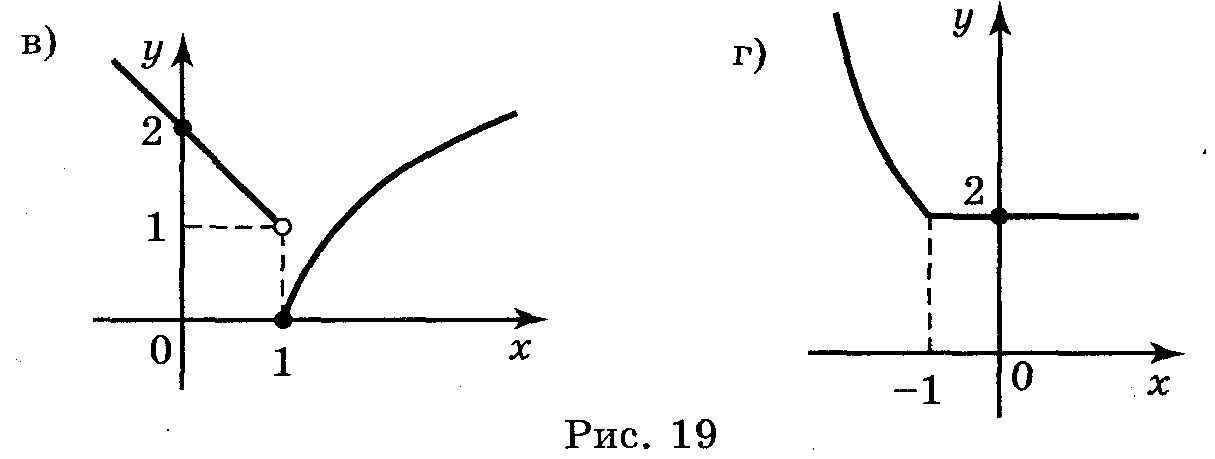
Рис 5
