Розв'язання
а)
Оскільки первісною для функції х5
є функція
,
то згідно з правилом 3 шукані первісні:
.
б) Оскільки однією із первісних для функції ех є функція ех, то згідно з правилом 3 маємо: F(x) = e2х-l + C.
Відповідь:
a)
;
б)
F(x) =
e2х-l
+ C.
Приклад
6. Знайдіть
.
Розв'язання
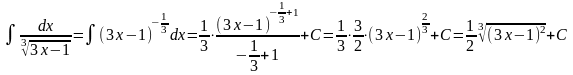
Відповідь:
.
2.Застосування первісної для відновлення рівняння руху точки
За допомогою первісної можна розв’язувати практичну задачу обернену до тієї, що ми розв’язували за допомогою похідної. Тобто, за допомогою первісної можна знаходити рівняння руху точки, якщо дано рівняння її швидкості.
Приклад1.
Точка
рухається із швидкістю
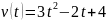. Знайти
шлях, який пройде тіло,
якщо в момент часу t=2c
тіло
пройшло
24
м.
Розв'язання
Оскільки фізичним змістом похідної є швидкість руху точки в даний момент часу, то фізичним змістом первісної функції ї шлях, який пройде матеріальна точка.
.
Задовільнимо початкові умови:
,
тоді
,
звідки
.
Отже,
,
(м)
№1. Знайдіть загальний вигляд первісних для функцій:
a)
f(x)
= 2х5
- 5х2;
б) f(x)=
+
в) f(x)
=
+ 3
;
г)
f(x)
= 5·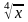
-
.
№ 2. Знайдіть загальний вигляд первісних для функцій:
a)
f(x)=5cosх-3sin
x;
б)
f(x)=2ex
+
3cos
x;
в)
f(x)=
+10x;
г)
f(x)=
-
.
№3. Для функції f(x) = 3х2 знайдіть первісну, графік якої проходить через точку А(0; 1).
№4.Знайдіть загальний вигляд первісних для. функцій:
a)
f(x)
= cos 2x + sin Зх;
б)
f(x)
=
.
№5.
Точка
рухається із швидкістю
. Знайти
шлях, який пройде тіло,
якщо в момент часу t=1c
тіло
пройшло
6
м.
П.2. Поняття криволінійної трапеції
Література:
1 Є.П.Нелін, О.Є.Долгова Алгебра і початки аналізу. Дворівневий підручник для 11 класу загальноосвітніх навчальних закладів (Харків. Світ дитинства. 2006)
2. О.М.Роганін. Плани-конспекти уроків
3.М.І. Шкіль, З.І.Слєпкань. Алгебра і початки аналізу.11
Методичні вказівки:
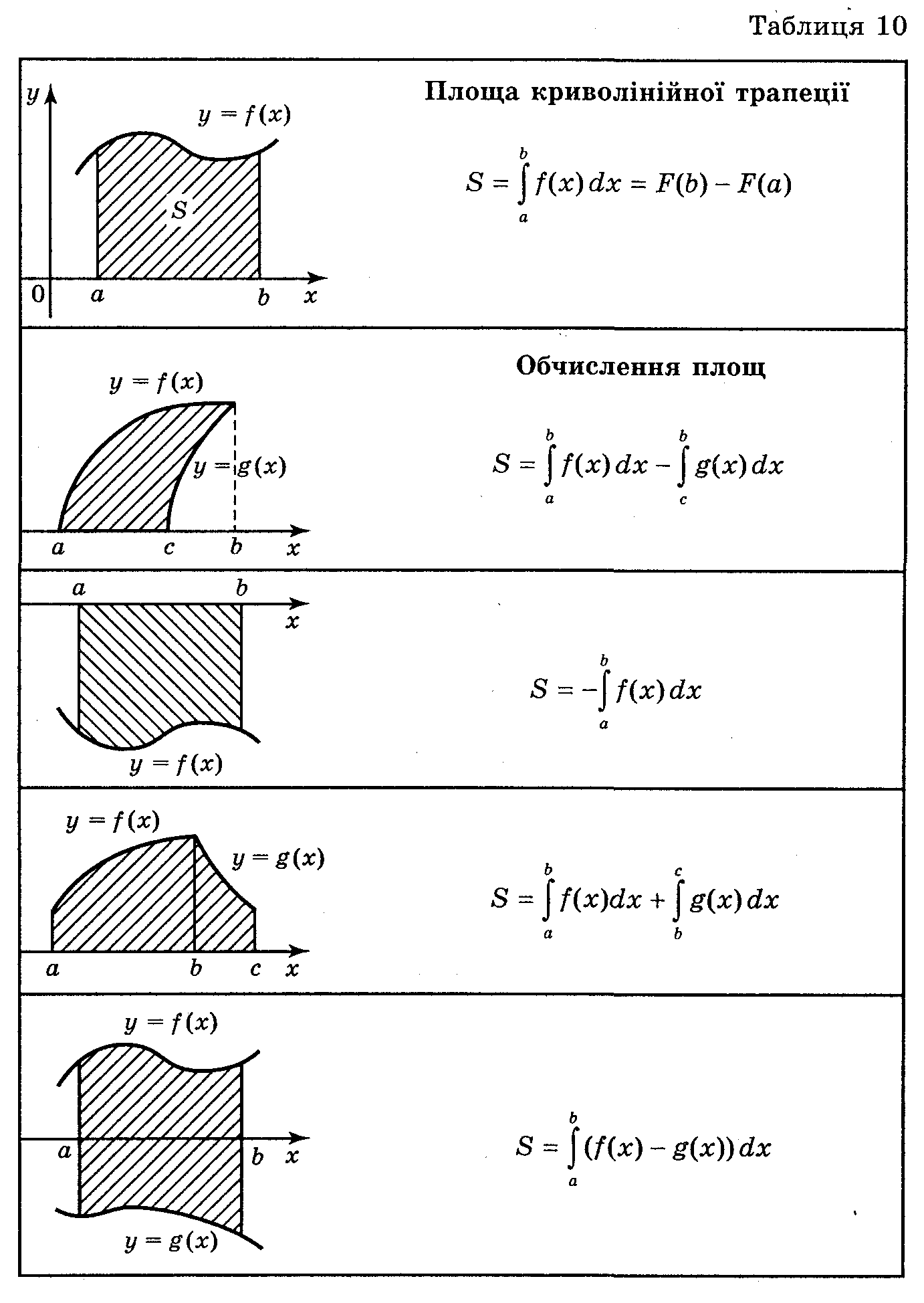
Студенти повинні вміти:
Розпізнавати та записувати формули для обчислення площ криволінійних трапецій та фігур, що за допомогою них виражаються.
Питання для самоконтролю:
Що називається криволінійною трапецією?
Самостійне вивчення з розробкою конспекту та розв’язуванням задач.
План.
Що таке криволінійна трапеція?
Площі фігур, які можна обчислити за допомогою криволінійних трапецій.
Форми поточного та підсумкового контролю самостійної роботи:
1.Поточний:
усне опитування
розв’язування задач.
2.Підсумковий:
тематична контрольна робота
державна підсумкова атестація
Лекційний матеріал до теми
На практиці часто доводиться обчислювати площі фігур, які не є криволінійними трапеціями.
Якщо треба обчислити площу фігури, обмежену декількома лініями, то знаходять криволінійні трапеції, переріз або об'єднання яких є дана фігура, обчислюють площі кожної із них і знаходять різницю або суму площ цих криволінійних трапецій.
К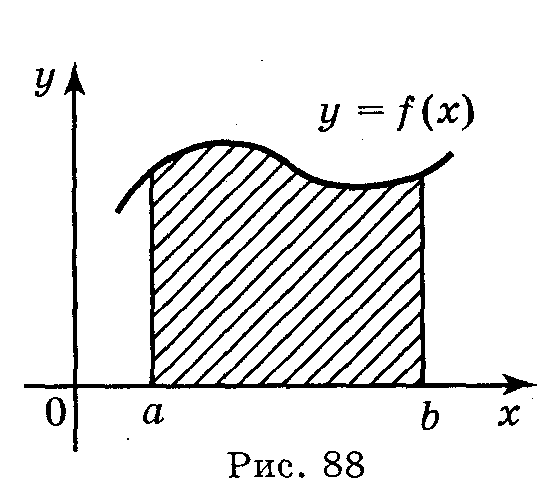
риволінійною
трапецією
називається фігура, обмежена графіком
неперервної функції у
= f(x),
яка не змінює знак на відрізку [а;
b],
прямими
x
= а,
х
= b
і відрізком [а;
b]
Приклад 1.
Побудуйте криволінійну трапецію,
обмежену лініями у
= cos
x,
у
= 0,
,
Р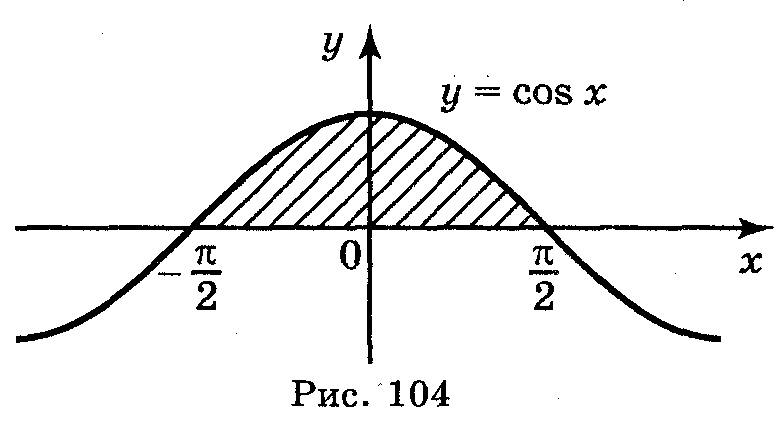
озв'язання
Криволінійну
трапецію зображено на рисунку. Одна із
первісних функції у=cosх
є F(x)
= sin
x,
тоді
Відповідь: 2.
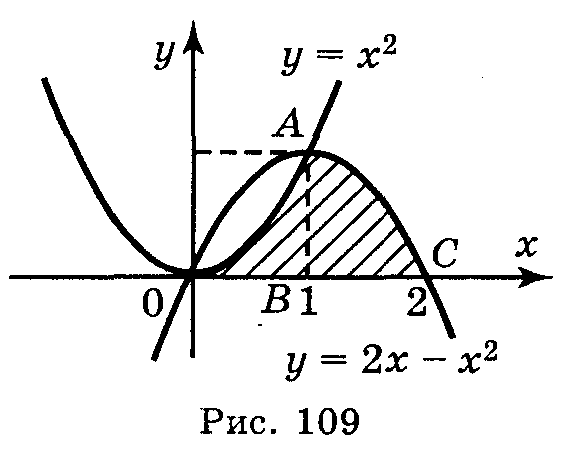
Приклад 3. Знайдіть площу фігури, обмеженої параболами у = х2 і у = 2х - х2 та віссю ОХ.
Розв'язання
Побудуємо графіки функцій у = х2 і у = 2х - х2 і знайдемо абсциси точок перетину цих графіків із рівняння: х2 = 2х – х2. Корені цього рівняння х1 = 0, х2 = 1. Дана фігура зображена на рис.
Із рисунка видно, що ця фігура складається з двох криволінійних трапецій: ОАВ і ВАС.
Отже, шукана площа
дорівнює сумі площ цих трапецій:
Відповідь: 1.
№1. Обчисліть (спочатку побудувавши рисунок) площу фігури, обмеженої лініями:
а) у = x2 + 1, у = x + 3;
б) у = 4 - х2, у = x + 2, у = 0
Відповідь:
а) 4,5; б) 6
2. Обчисліть площу фігури, обмеженої лініями:
а) у = х3, у - 2х - х2, у = 0; б) у = , у = х;
в) у = , у = 2 - х2, х = 1, у = 0; г) у = х3, у = .
Відповідь:
а)
;
б)
;
в) 2
г)
.
3. Обчисліть площу фігури, обмеженої лініями:
а) у = х2; у = 2х2 - 1 б) у = х2 - 2х + 2, у = 2 + 4х - х2.
Відповідь:
а)
;
б) 9.
4. Знайдіть площу фігури, обмеженої лініями:
а)
у = eх,
у = е-x,
у = e;
б) y
= sinx,
y
= cosx,
.
Відповіді: а) 2; б) 2 - .