- •П.1. Поняття функціональної залежності, числова функція.
- •Лекційний матеріал до теми.
- •1.Історія виникнення поняття функції.
- •3. Числова функція. Область визначення функції.
- •4. Способи задання функції
- •П.2. Неперервність функцій. Типи розривів числових функцій
- •Лекційний матеріал до теми.
- •1. Неперервність функцій.
- •2. Типи розривів числових функцій
- •Тема 2. Степенева, показникова і логарифмічна функції. П.1. Логарифмування та потенціювання виразів
- •Лекційний матеріал до теми.
- •Логарифмування виразів
- •Розв'язання
- •2.Потенціювання виразів.
- •Розв'язання
- •Тема 3 . Тригонометричні функції. П.1. Формули половинного аргументу, формули потрійного аргументу
- •Лекційний матеріал до теми.
- •1. Формули половинного аргументу
- •2.Формули потрійного аргументу
- •Тема 4 . Рівняння, нерівності та їхні системи. П.1.Розв’язування задач, що приводять до розв’язування рівнянь та систем рівнянь
- •Лекційний матеріал до теми.
- •Хімічні задачі
- •Задачі на рух.
- •Задачі, в яких кількість невідомих більша за кількість рівнянь системи.
- •Тема 5 . Вектори і координати. П.1. Вектори в просторі. Дії над векторами. Розклад вектора на складові
- •Лекційний матеріал до теми.
- •1.Вектори в просторі. Дії над векторами.
- •Розклад вектора на складові.
- •Тема 6 . Систематизація та узагальнення фактів і методів планіметрії.
- •Лекційний матеріал до теми.
- •1.Формула площі трикутника за двома сторонами і кутом між ними.
- •2. Формула площі трикутника за стороною і опущеною до неї висотою.
- •3.Формула Герона
- •4.Формули площ трикутника з використанням радіусів вписаного та описаного навколо трикутника кола
- •Тема 7 . Паралельність та перпендикулярність прямих і площин у просторі.
- •1.Взаємне розміщення двох прямих у просторі
- •Лекційний матеріал до теми.
- •Взаємне розміщення двох прямих у просторі
- •2.Теорема про існування і єдиність прямої, яка проходить через дану точку і паралельна даній прямій
- •Ознака паралельності прямих
- •Доведення
- •П.2. Теореми про паралельні площини
- •Лекційний матеріал до теми
- •2. Теорема про відрізки паралельних прямих, які містяться між двома паралельними площинами
- •Доведення
- •Розв'язання
- •П.3. Ознака перпендикулярності двох прямих в просторі
- •Лекційний матеріал до теми
- •Тема 8. Похідна та її застосування.
- •Лекційний матеріал до теми
- •П.2. Дослідження функції на екстремум за допомогою другої похідної
- •Лекційний матеріал до теми
- •Тема 9. Інтеграл та його застосування п.1. Правила знаходження первісної. Фізичні застосуванні первісної функції
- •Лекційний матеріал до теми
- •Правила знаходження первісних
- •Розв'язання
- •Розв'язання
- •2.Застосування первісної для відновлення рівняння руху точки
- •Розв'язання
- •П.2. Поняття криволінійної трапеції
- •Лекційний матеріал до теми
- •П.3. Застосування визначеного інтегралу в економіці, техніці, фізиці.
- •Лекційний матеріал до теми
- •П.4. Рівняння гармонійних коливань
- •Лекційний матеріал до теми
- •Тема 10. Многогранники. Об’єми та площі поверхонь многогранників п.1. Вимірювання відстаней у просторі. Вимірювання кутів у просторі. Двогранний кут
- •Лекційний матеріал до теми
- •1. Вимірювання відстаней у просторі.
- •Задача з точки м опустити перпендикуляр на пряму ав
- •2 . Поняття двогранного кута та його елементів, лінійного кута двогранного кута
- •Задача 3*
- •Задача 4*
- •Тема 11. Тіла обертання. Об’єми та площі поверхонь тіл обертання
- •Лекційний матеріал до теми
- •1. Комбінації многогранників
- •Задача1
- •Розв'язання
- •2.Комбінації многогранників і циліндра
- •3.Комбінації многогранників і конуса
- •4.Комбінації многогранників і кулі
- •5. Куля і конус
- •6. Куля і циліндр
- •7. Конус і циліндр
- •Тема 12. Елементи теорії ймовірностей і математичної статистики
- •Лекційний матеріал до теми
- •Тема 13. Повторення, узагальнення та систематизація навчального матеріалу, розв’язування задач.
- •Лекційний матеріал до теми
- •4. Геометрична прогресія.
- •Література
Розклад вектора на складові.
Означення. Вектори а1, а2, …, аn називаються лінійно незалежними, якщо рівність
 (1)
(1)
виконується лише
при
 .
.
Нехай
вектори
 такі, що за напрямом збігаються
відпо-
відно з осями Ох,
Оу,
Оz.
Тобто вони лінійно незалежні і
такі, що за напрямом збігаються
відпо-
відно з осями Ох,
Оу,
Оz.
Тобто вони лінійно незалежні і
 .
Такі вектори надалі називатимемо
одиничними
базисними векторами осей системи
координат.
.
Такі вектори надалі називатимемо
одиничними
базисними векторами осей системи
координат.
Тоді
будь – який вектор можна представити
у вигляді лінійної комбінації базисних
векторів
 ,
де ax
,ay
,az
- координати
нашого вектора в заданому базисі.
,
де ax
,ay
,az
- координати
нашого вектора в заданому базисі.
Приклад1.
В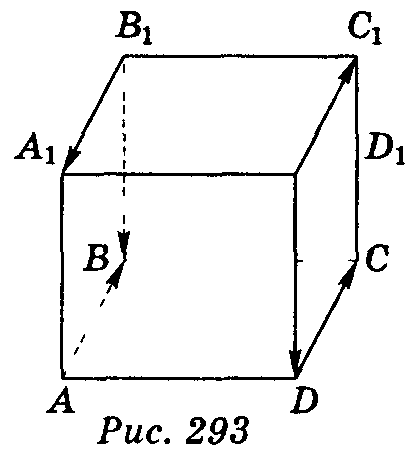 казати
однаково напрямлені, протилежно
напрямлені вектори серед векторів, які
вказані на зображенні прямокутного
паралелепіпеда
казати
однаково напрямлені, протилежно
напрямлені вектори серед векторів, які
вказані на зображенні прямокутного
паралелепіпеда
Приклад 2. Дано вектори (4; -5; 6), (-1; 2; 5). Знайдіть: + , – , | + |, | – |.
Розв’язання.
1. + =(4; -5; 6)+(-1; 2; 5)= (3;-3;11);
2. - =(4; -5; 6)-(-1; 2; 5)= (5;-7;1);
3.
|
+
|= =
=
4.
|
–
|=
Приклад 3. Чи колінеарні вектори (2; 3; 8) і (-4; 6; - 16) ?
Розв’язання.
Відповідні координати колінеарних векторів пропорційні. Перевіримо це для наших векторів:
 ,
отже вектори не колінеарні.
,
отже вектори не колінеарні.
Приклад
4.
Спростіть:
+ +
+
+
+
+
+ +
+
Розв’язання
+
= =
-
,
тоді
+
+
=0,
крім того
+
=0,
отже,
+
+
+
+
+
=
=
-
,
тоді
+
+
=0,
крім того
+
=0,
отже,
+
+
+
+
+
=
№1. Чи лежать на одній прямій точки А, В, С, якщо А(3; -7; 8), В(-5; 4; 1), С (27; -40; 29)?
№2. Знайдіть координати точки С такої, що СА + СВ = 0, якщо А(-5; 7; 12), В(4; -8; 3).
№3.
Знайдіть координати векторів
і
,
якщо
=
+
,
 =
–
,
(4;
-1; 5),
(6;
3; 1).
=
–
,
(4;
-1; 5),
(6;
3; 1).
№4. Чи може бути нульовим вектором сума трьох векторів, модулі яких дорівнюють 7; 1; 8?
№5.
Спростіть:
+ +
+ +
+
+
+ +
.
+
.
№6. Чи колінеарні вектори АВ і CD, якщо А(3; -2; 5), B(-1; 4; 7), C(1; 3; 6), D(-3; 9; 18)?
№7. При яких значеннях т і п вектори АВ і CD колінеарні, якщо A(1; 0; 2), B(3; n; 5), C(2; 2; 0), D(5; 4; m)?
Тема 6 . Систематизація та узагальнення фактів і методів планіметрії.
П.1. Різні формули площ трикутників
Література:
1. Г.В.Апостолова Геометрія : 9 : дворівн. підруч. для загальноосвіт. навч. закл. / Г.В.Апостолова. – К. : Генеза, 2009. – 304 с.
2. М.І.Бурда, Н.А.Тарасенкова Геометрія. 9 клас: Підруч. для загальноосвіт. навч. закл. / М.І.Бурда, Н.А.Тарасенкова. - К.: «Зодіак-Еко», 2009
3. О.М.Роганін. Плани-конспекти уроків
Методичні вказівки:
Площі фігур |
||||
Прямокутник
S = ab, S = d2sinφ |
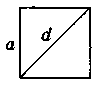
Квадрат
S = a2, S = d2 |
|||
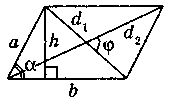
Паралелограм
S = bh, S = absinα S = d1d2 sinφ |
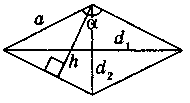
Ромб
S = ah, S = a2sina S = d1d2 |
|||
Трикутник |
||||
S
=
aha
де
|
S = pr |
S = absina |
||
|
|
|||
Трапеція
S
=
|
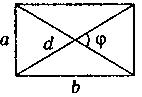
Довільний чотирикутник
S = d1d2sinφ |
|||
Студенти повинні вміти:
Обчислювати площі плоских фігур використовуючи різноманітні формули площ трикутників
Питання для самоконтролю:
Що таке площа? Сформулюйте властивості площі.
Чому дорівнює площа прямокутника?
Чому дорівнює площа квадрата зі стороною а?
Як зміниться площа прямокутника, якщо:
а) зменшити одну сторону вдвічі, а другу сторону залишити без змін;
б) кожну сторону збільшити вдвічі?
Заповніть пропуски: 1км2 = ... м2; 1 м2 = ... см2; 1см2 = ... мм2; 1 га = ... м2; 1 а = ... м2.
Чому дорівнює площа паралелограма?
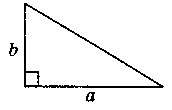
Чому дорівнює площа трикутника, якщо відома його сторона а та висота па, проведена до неї?
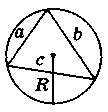
Як можна знайти площу трикутника, якщо відомі його сторони і радіус описаного кола?
Як можна знайти площу трикутника, якщо відомі його сторони і радіус вписаного кола?
Самостійне вивчення з розробкою конспекту та розв’язуванням задач.
План.
1.Формула площі трикутника за двома сторонами і кутом між ними.
2. Формула площі трикутника за стороною і опущеною до неї висотою.
3.Формула Герона.
4.Формули площ трикутника з використанням радіусів вписаного та описаного навколо трикутника кола.
Форми поточного та підсумкового контролю самостійної роботи:
Поточний:
перевірка конспектів
усне опитування
розв’язування задач.
Підсумковий:
тематична контрольна робота
державна підсумкова атестація

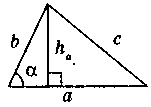
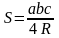


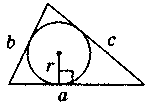

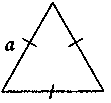

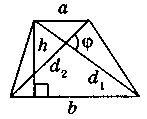
 ∙h,
S
=
d1d2sinφ
∙h,
S
=
d1d2sinφ