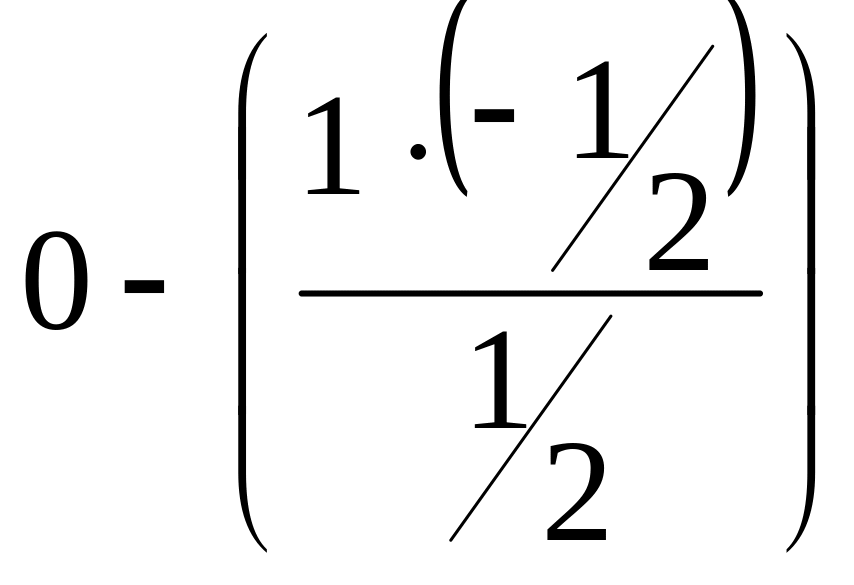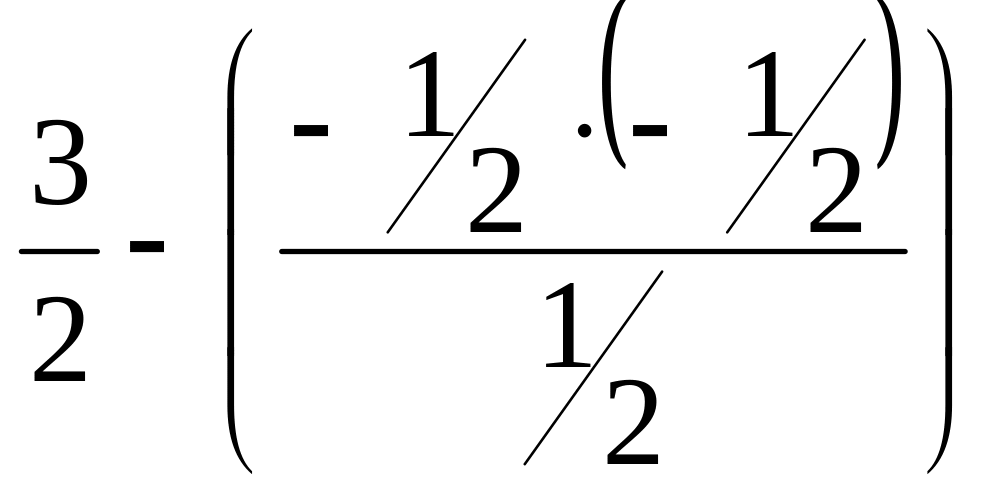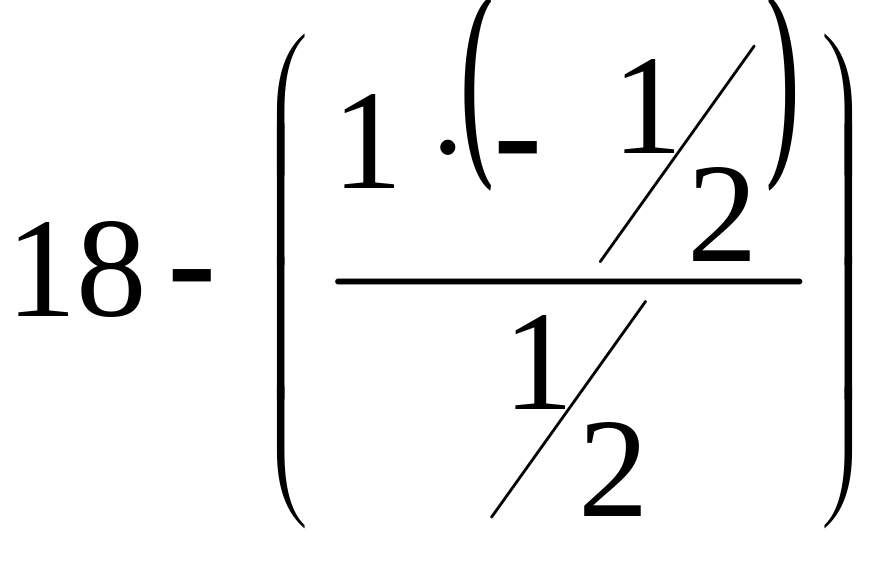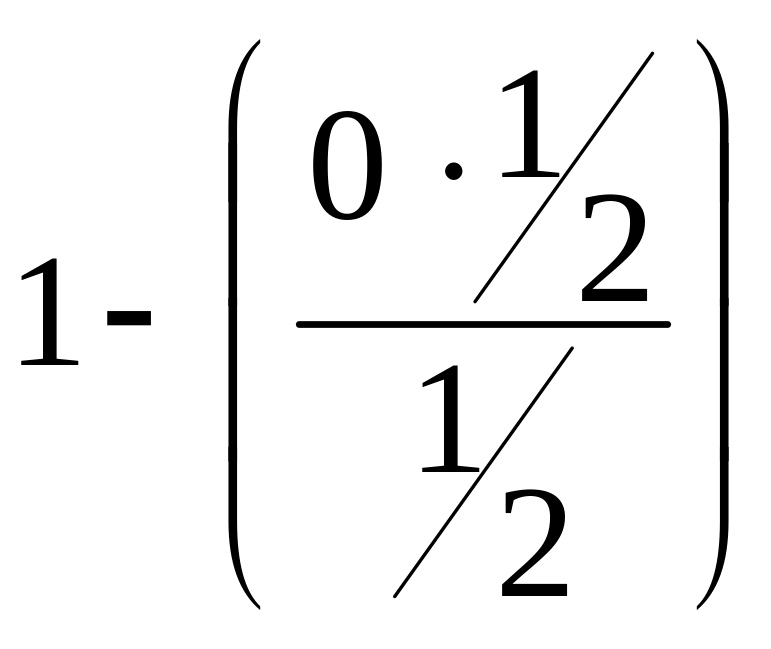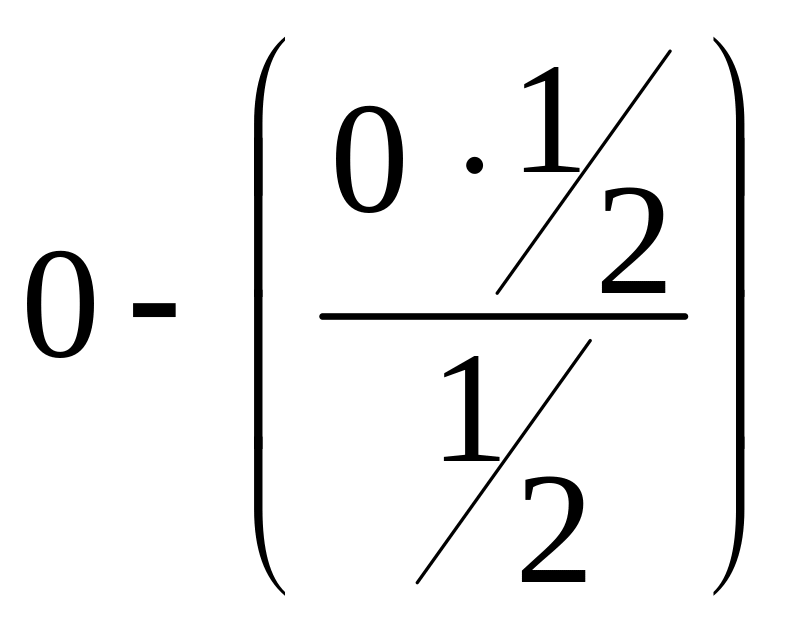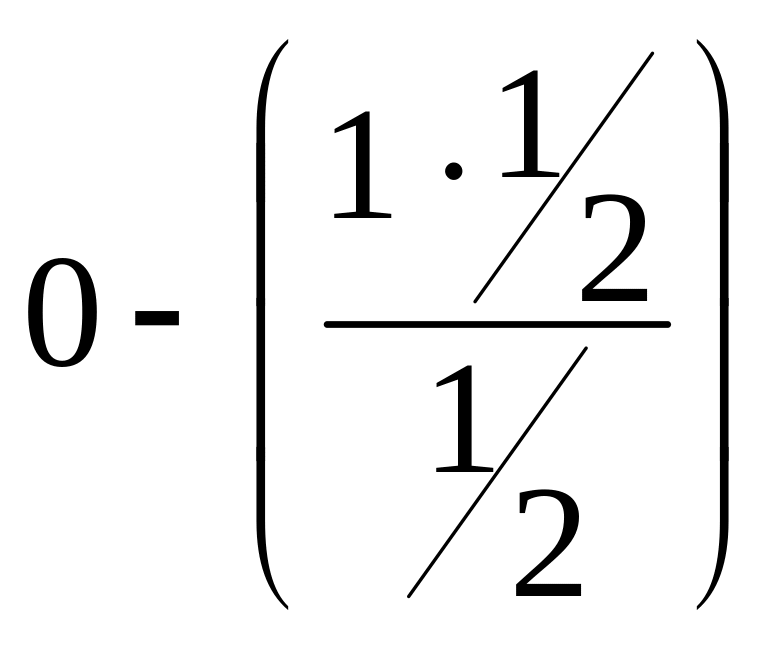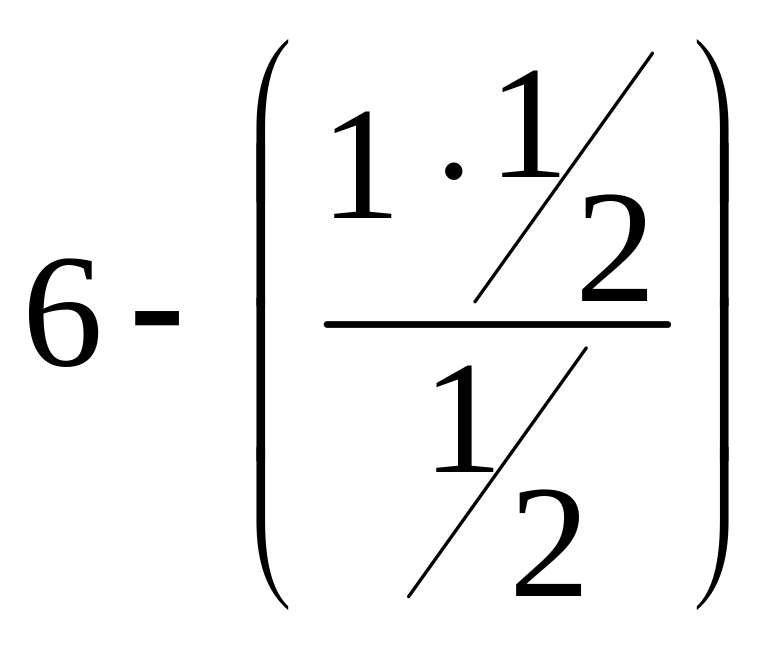Задачи для самостоятельного решения

Задачи линейного программирования привести к каноническому виду:

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.
11.	12.
13.	14.
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.
27.	28.
29.	30.

Глава 4. Симплексный метод решения задач линейного программирования

4.1.Общая идея симплексного метода

Для начала работы требуется, чтобы заданная система ограничений выражалась равенствами, причем в этой системе ограничений должны быть выделены базисные неизвестные. Решение задачи при помощи симплекс-метода распадается на ряд шагов. На каждом шаге от данного базиса Б переходят к другому, новому базису Б¹  с таким расчетом, чтобы значение функции F увеличивалось при поиске на максимум или уменьшалось при поиске на минимум целевой функции. Для перехода к новому базису из старого базиса выводится одна из переменных и вместо нее вводится другая из числа свободных. После конечного числа шагов находится некоторый базис Б^(k) , для которого есть искомый максимум или минимум целевой линейной функции F, а соответствующее базисное решение является оптимальным либо выясняется, что задача не имеет решения.

4.2.Табличный симплексный метод

Приведем алгоритм решения задачи линейного программирования на отыскание максимума с помощью симплекс таблиц.

F = с₁х₁+с₂х₂+…+с_nx_nmax

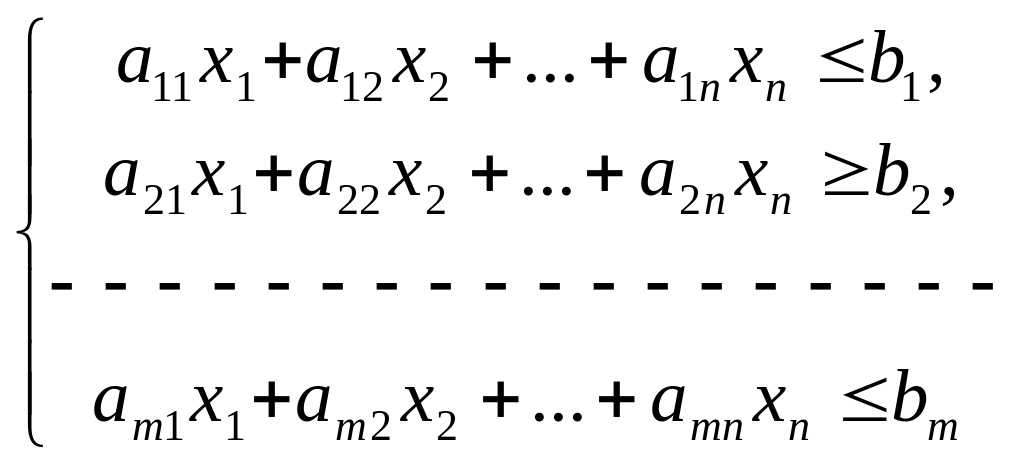
х₁0, х₂0,…, х_n0.

1-й шаг.

Приводим задачу линейного программирования к стандартной форме первого или второго вида в зависимости от направления целевой функции.

При решении на максимум:

F = с₁х₁+с₂х₂+…+с_nx_nmax

х₁0, х₂0,…, х_n0.

Вводим добавочные переменные и записываем полученную систему уравнений и линейную функцию в виде расширенной системы:

F–c₁x₁–c₂x₂–…–c_nx_n=0=c_о.

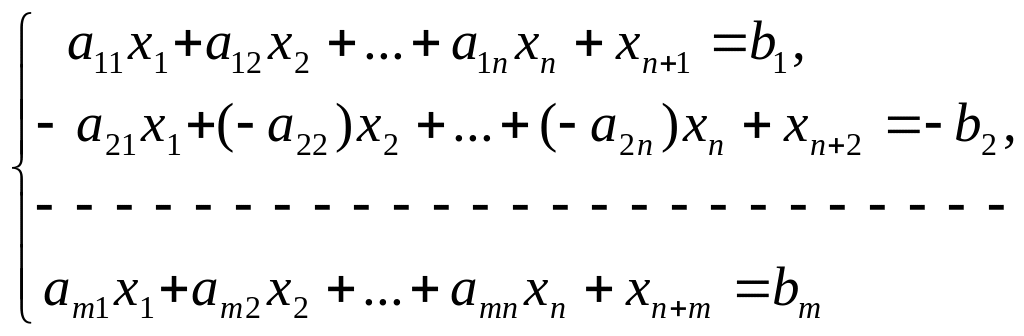
При решении на минимум:

F = с₁х₁+с₂х₂+…+с_nx_nmin

Вводим добавочные переменные и записываем полученную систему уравнений и линейную функцию в виде расширенной системы:

F=c₁x₁+c₂x₂+…+c_nx_n=0=c_о.

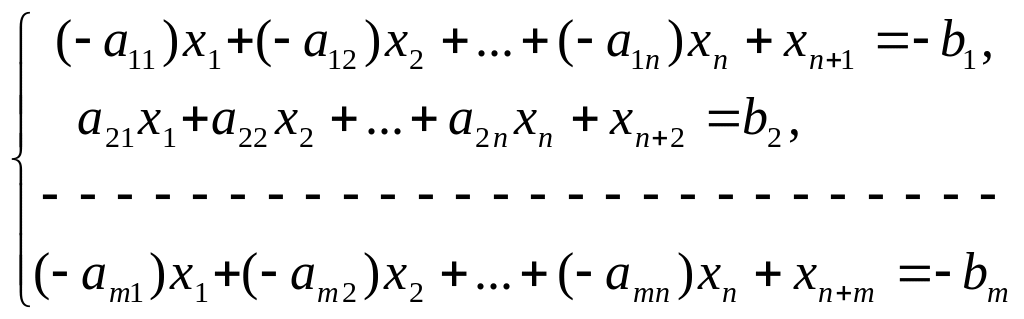
2-й шаг.

Составляем первоначальную симплекс-таблицу.

При решении на максимум:

Переменные базис	х1	х2	…	xn	хn+1	хn+2	…	хm+n	свободные члены bj	оценочные отношения
xn+1	a11	a12	…	a1n	1	0	…	0	b1
xn+1	a21	a22	…	a2n	0	1	…	0	b2
…	…	…	…	…	0	0	…	0
xm+n	am1	am2	…	amn	0	0	0	1	bm
F	–c1	–c2	…	–cn	0	0	0	0	С0

При решении на минимум:

Переменные базис	х1	х2	…	xn	хn+1	хn+2	…	хm+n	свободные члены bj	оценочные отношения
xn+1	a11	a12	…	a1n	1	0	…	0	b1
xn+1	a21	a22	…	a2n	0	1	…	0	b2
…	…	…	…	…	0	0	…	0
xm+n	am1	am2	…	amn	0	0	0	1	bm
F	c1	c2	…	cn	0	0	0	0	С0

Обратите внимание на целевую строку:

При поиске на максимум коэффициенты целевой функции при занесении в таблицу меняют знак на противоположный, а при поиске на минимум остаются без изменения.

Классификация симплексных таблиц.

• Симплексная таблица называется прямо допустимой, если . Прямо-допустимая симплекс-таблица соответствует допустимому базисному решению.

• Симплексная таблица называется двойственно допустимой, если .

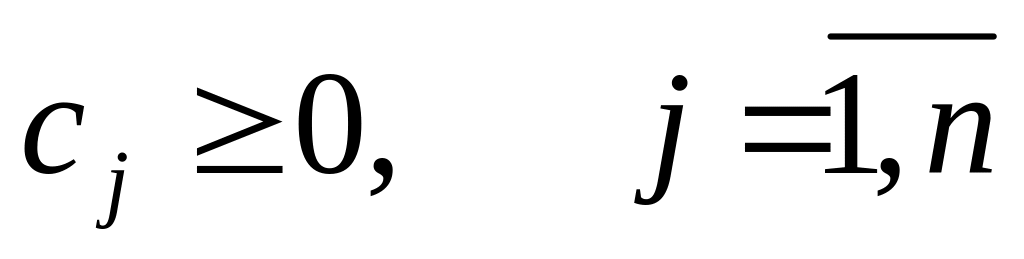• Симплексная таблица называется оптимальной, если она одновременно и прямо допустимая, и двойственно допустимая. Оптимальная симплекс-таблица соответствует оптимальному базисному решению.

3-й шаг.

Проверяем выполнение критерия оптимальности.

При решении на максимум:

• Наличие в целевой (последней) строке отрицательных коэффициентов.

• Если в целевой (последней) строке отрицательных коэффициентов нет, то решение оптимально и F^*=С₀, базисные переменные равны соответствующим коэффициентам b_j, остальные переменные равны нулю, т. е. X^*=( 0, …, 0, b₁,b₂,…, b_m).

• Если критерий оптимальности не выполнен (в целевой (последней) строке есть отрицательные коэффициенты), то наибольший по модулю отрицательный коэффициент в последней строке, определяет разрешающий столбец S. В случае, когда в целевой строке несколько одинаковых наибольших по модулю отрицательных коэффициентов, выбирается любой.

При решении на минимум:

• Наличие в целевой (последней) строке положительных коэффициентов.

• Если в целевой (последней) строке положительных коэффициентов нет, то решение оптимально и F^*=С₀, базисные переменные равны соответствующим коэффициентам b_j, остальные переменные равны нулю, т. е. X^*=( 0, …, 0, b₁,b₂,…, b_m).

• Если критерий оптимальности не выполнен (в целевой (последней) строке есть положительные коэффициенты), то наибольший положительный коэффициент в последней строке, определяет разрешающий столбец S. В случае, когда в целевой строке несколько одинаковых наибольших положительных коэффициентов, выбирается любой.

4-й шаг.

Последующие шаги одинаковы для решения на максимум и минимум.

Для определения разрешающей строки, рассчитаем оценочные отношения и заполняем последний столбец таблицы.

Оценочное отношение i-ой строки равно

1. , если b_i и a_is имеют разные знаки;

2. , если b_i =0 и а_is<0;

3. , если a_is=0;

4. 0, если b_i=0 и а_is>0;

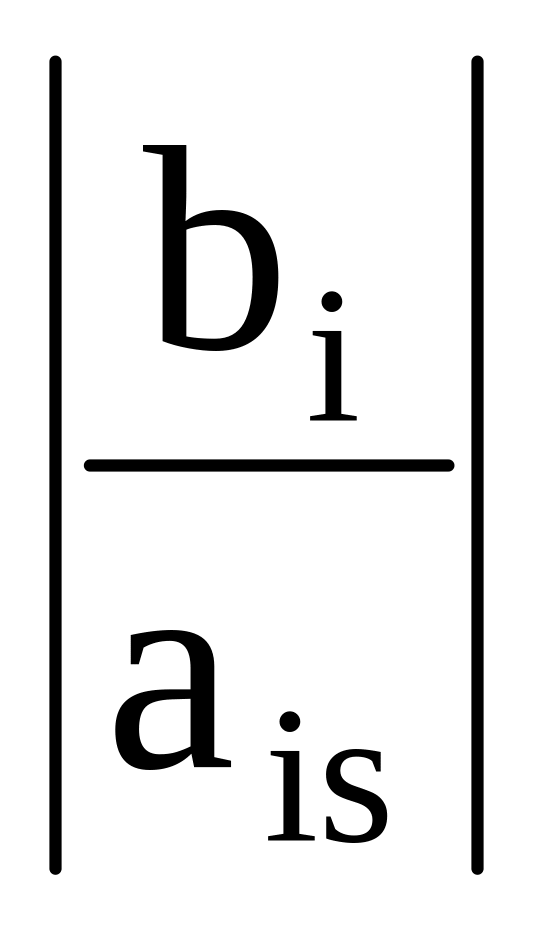5. , если b_i и a_is имеют одинаковые знаки.

В столбце оценочных отношений находим минимальный элемент min который определяет разрешающую строку g. Если невозможно найти ведущую строку, так как нет положительных элементов в ведущем столбце, то функция в области допустимых решений задачи не ограничена - алгоритм завершает работу.

На пересечении разрешающих строки и столбца находится разрешающий элемент аgs.

5-й шаг.

Строим следующую таблицу.

Правила преобразований симплексной таблицы.

При составлении новой симплекс-таблицы в ней происходят следующие изменения:

• вместо базисной переменной х_g записываем х_s;  

• ведущий элемент заменяется на обратную величину a_g,s'= 1/a_g,s ;

• все элементы ведущего столбца (кроме a_g,s) умножаются на -1/a_g,s;

• все элементы ведущей строки (кроме a_g,s) умножаются на 1/a_g,s;

• оставшиеся элементы симплекс-таблицы преобразуются по формуле Жордана-Гаусса:

Схему преобразования элементов симплекс-таблицы (кроме ведущей строки и ведущего столбца) называют схемой ”прямоугольника” (рисунок 1).

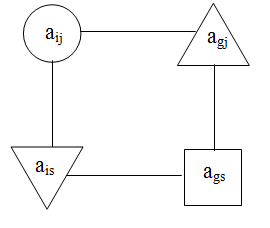
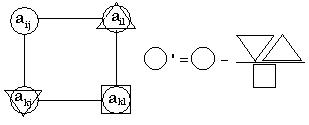
Рис. 1. Схему преобразования элементов симплекс-таблицы

Преобразуемый элемент a_i,j и соответствующие ему три сомножителя как раз и являются вершинами ”прямоугольника”.

После заполнения всей таблицы переходим к третьему шагу (начало новой итерации).

Пример №1

Решим задачу линейного программирования на максимум симплексным методом, с использованием симплексной таблицы.

Определим значение целевой функции

при следующих ограничениях:

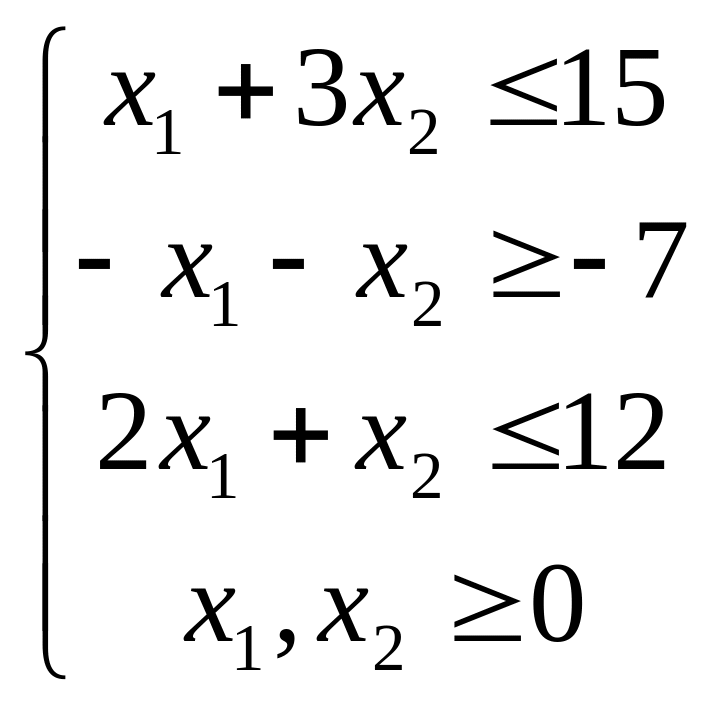
Решение:

1-й шаг.

Приводим задачу линейного программирования к стандартной форме. Так как ищем максимум целевой функции, то все неравенства должны быть вида (≤). Второе неравенство не удовлетворяет это условие, значит, умножим его на (-1).

Тогда получим систему неравенств вида:

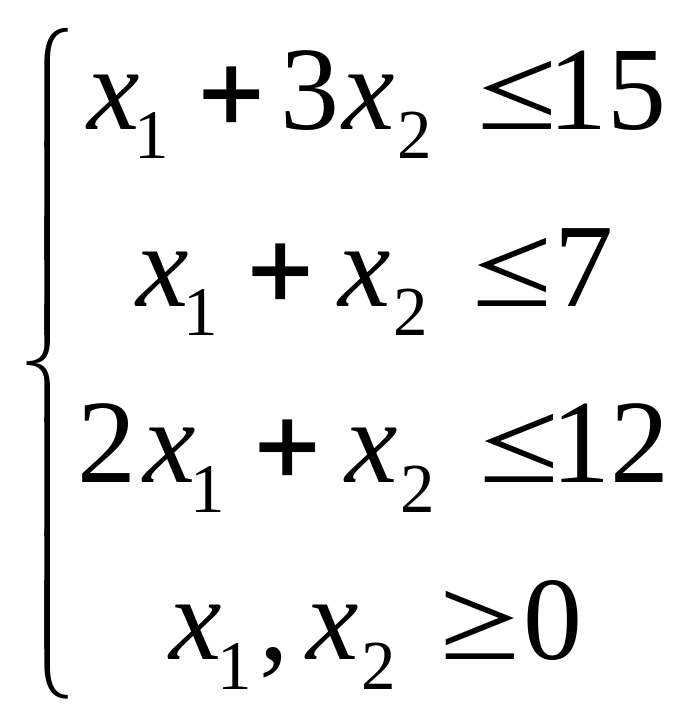
Приведем систему неравенств к системе уравнений путем введения дополнительных переменных:

В 1-м неравенстве вводим базисную переменную x₃.

В 2-м неравенстве вводим базисную переменную x₄.

В 3-м неравенстве вводим базисную переменную x₅.

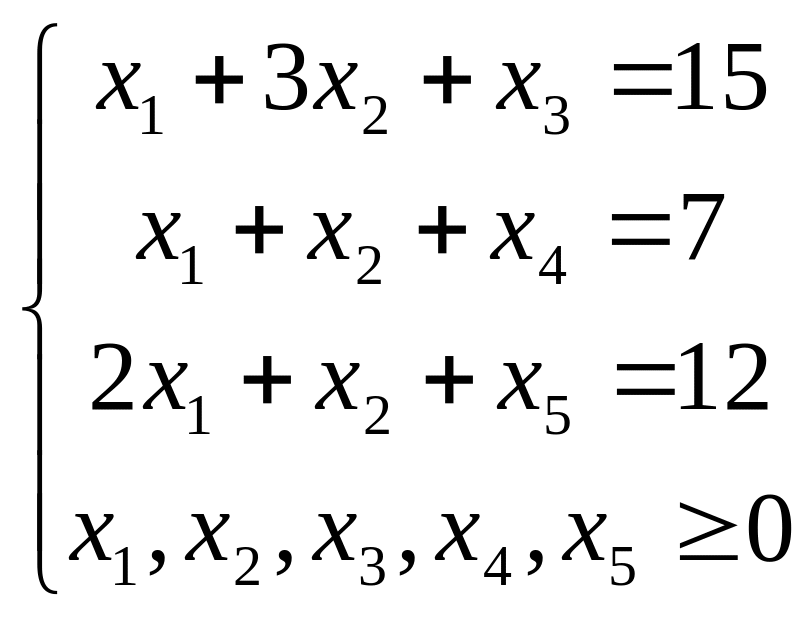
Представим систему в расширенном виде:

1x₁ + 3x₂ + 1x₃ + 0x₄ + 0x₅ = 15

1x₁ + 1x₂ + 0x₃ + 1x₄ + 0x₅ = 7

2x₁ + 1x₂ + 0x₃ + 0x₄ + 1x₅ = 12

2-й шаг.

Заполним таблицу

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b
x3	1	3	1	0	0	15
x4	1	1	0	1	0	7
x5	2	1	0	0	1	12
F	-3	-2	0	0	0	0

3-й шаг. Итерация №1.

Переходим к основному алгоритму симплекс-метода.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x₁(s=1), так как это наибольший по модулю отрицательный коэффициент.

4-й шаг.

Определяем разрешающую строку, для этого вычислим значения оценочного отношения по строкам b_i / a_i1 и из них выберем наименьшее:

min (15 : 1 , 7 : 1 , 12 : 2 ) = 6

Следовательно, 3-ая строка является ведущей.

Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b	Оценочное отношение
x3	1	3	1	0	0	15	15
x4	1	1	0	1	0	7	7
x5	2	1	0	0	1	12	6	min
F	-3	-2	0	0	0	0
	max

5-й шаг.

Получаем новую симплекс-таблицу:

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b
x3	0
x4	0
x1	1
F	0

Приведем к окончательному виду:

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b
x3	0	21/2	1	0	-1/2	9
x4	0	1/2	0	1	-1/2	1
x1	1	1/2	0	0	1/2	6
F	0	-1/2	0	0	11/2	18

6-й шаг. Итерация №2.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент по модулю. Вычислим значения оценочного отношения по строкам как частное от деления: b_i / a_i2 и из них выберем наименьшее: min (9 : 5/2 , 1 : 1/2 , 6 : 1/2 ) = 2

Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (1/2) и находится на пересечении ведущего столбца и ведущей строки.

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b	Оценочное отношение
x3	0	21/2	1	0	-1/2	9	18/5
x4	0	1/2	0	1	-1/2	1	2
x1	1	1/2	0	0	1/2	6	12
F	0	-1/2	0	0	11/2	18

Получаем новую симплекс-таблицу:

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b
x3		0
x2		1
x1		0
F		0

Приведем к окончательному виду:

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b
x3	0	0	1	-5	2	4
x2	0	1	0	2	-1	2
x1	1	0	0	-1	1	5
F	0	0	0	1	1	19

Конец итераций: индексная строка не содержит отрицательных элементов - найден оптимальный план. Оптимальный план можно записать так:

x1 = 5

x2 = 2

F(X) =

Пример №2

Решим задачу линейного программирования на минимум симплексным методом, с использованием симплексной таблицы.

Определим значение целевой функции

при следующих ограничениях:

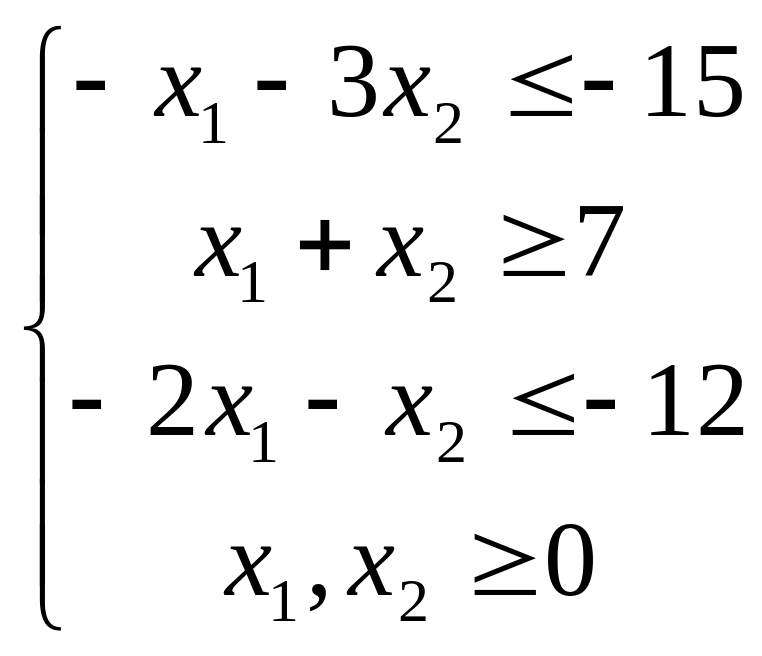
Решение:

1-й шаг.

Приводим задачу линейного программирования к стандартной форме. Так как ищем минимум целевой функции, то все неравенства должны быть вида ( ). Первое и третье неравенства не удовлетворяют это условие, значит, умножим их на (-1).

Тогда получим систему неравенств вида:

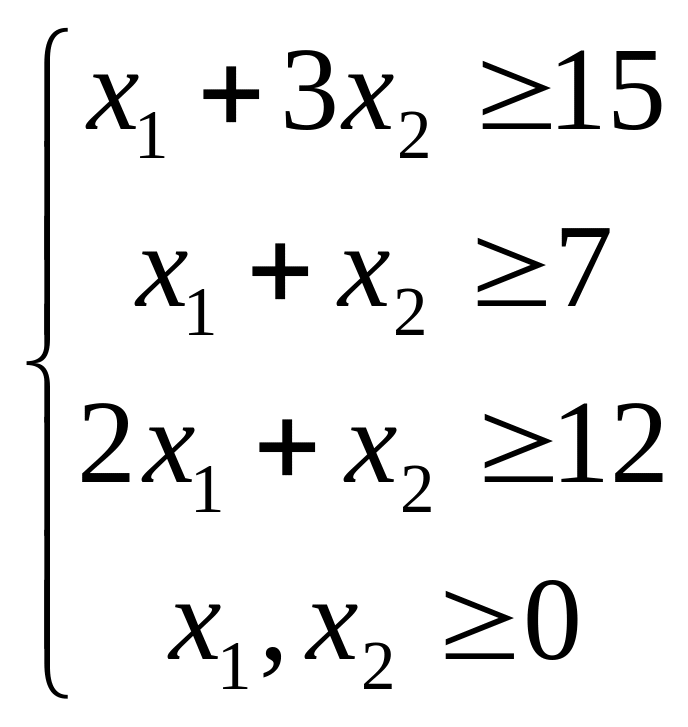
Приведем систему неравенств к системе уравнений путем введения дополнительных переменных:

В 1-м неравенстве вводим базисную переменную x₃.

В 2-м неравенстве вводим базисную переменную x₄.

В 3-м неравенстве вводим базисную переменную x₅.

Представим систему в расширенном виде:

1x₁ + 3x₂ + 1x₃ + 0x₄ + 0x₅ = 15

1x₁ + 1x₂ + 0x₃ + 1x₄ + 0x₅ = 7

2x₁ + 1x₂ + 0x₃ + 0x₄ + 1x₅ = 12

2-й шаг.

Заполним таблицу

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b	Оценочное отношение
x3	1	3	1	0	0	15
x4	1	1	0	1	0	7
x5	2	1	0	0	1	12
F	3	2	0	0	0	0

3-й шаг. Итерация №1.

Переходим к основному алгоритму симплекс-метода. Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x₁(s=1), так как это наибольший положительный коэффициент.

4-й шаг.

Определяем разрешающую строку, для этого вычислим значения оценочного отношения по строкам b_i / a_i1 и из них выберем наименьшее: min (15 : 1 , 7 : 1 , 12 : 2 ) = 6.

Следовательно, 3-ая строка является ведущей. Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b	Оценочное отношение
x3	1	3	1	0	0	15	15
x4	1	1	0	1	0	7	7
x5	2	1	0	0	1	12	6
F	3	2	0	0	0	0

5-й шаг.

Получаем новую симплекс-таблицу:

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b	Оценочное отношение
x3	0
x4	0
x5	1
F	0

Приведем к окончательному виду:

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b	Оценочное отношение
x3	0	21/2	1	0	-1/2	9
x4	0	1/2	0	1	-1/2	1
x1	1	1/2	0	0	1/2	6
F	0	1/2	0	0	-11/2	-18

6-й шаг. Итерация №2.

Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это положительный коэффициент.

Вычислим значения оценочного отношения по строкам как частное от деления: b_i / a_i2 и из них выберем наименьшее:

min (9 : 2¹/₂ , 1 : ¹/₂ , 6 : ¹/₂ ) = 2

Следовательно, 2-ая строка является ведущей.

Разрешающий элемент равен (1/2) и находится на пересечении ведущего столбца и ведущей строки.

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b	Оценочное отношение
x3	0	21/2	1	0	-1/2	9	33/5
x4	0	1/2	0	1	-1/2	1	2
x1	1	1/2	0	0	1/2	6	12
F	0	1/2	0	0	-11/2	-18

Получаем новую симплекс-таблицу:

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b
x3		0
x2		1
x1		0
F		0

Приведем к окончательному виду:

Переменные Базис	x1	x2	x3	x4	x5	Свободные члены b
x3	0	0	1	-5	2	4
x2	0	1	0	2	-1	2
x1	1	0	0	-1	1	5
F	0	0	0	-1	-1	-19

Конец итераций: индексная строка не содержит положительных элементов - найден оптимальный план, который можно записать так:

x1 = 5

x2 = 2

F=-19

Отрицательный результат означает, что вместо расходов получим доход, что доказывается проверкой.

Проверяем:

F(X) = .