Задачи для самостоятельного решения

Задачи линейного программирования решить графическим методом:

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.
11.
13.	14.
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.
27.	28.
29.	30.

Глава 3. Стандартная и каноническая формы задачи линейного программирования

Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалента минимизации той же функции, взятой с противоположным знаком, и наоборот.

• Первая стандартная форма задачи линейного программирования имеет вид:

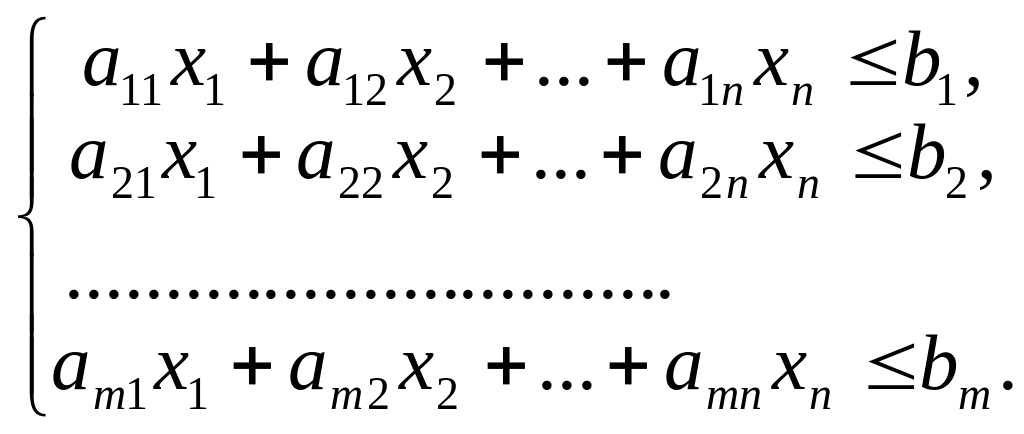
• Вторая стандартная форма задачи линейного программирования имеет вид:

• Канонической формой задачи линейного программирования называется задача вида:

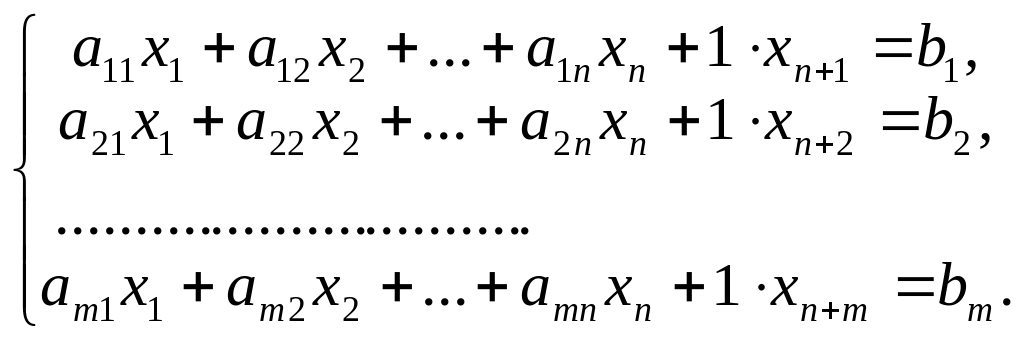
Ппроцесс приведения задачи линейного программирования к каноническому виду состоит в следующем:

1) Изменение вида целевой функции.

Если в исходной задаче требуется определить максимум линейной функции, то следует изменить знак и искать минимум этой функции.

Дано

Меняем знаки

Получаем

Это справедливо и для обратного преобразования из min в max.

2)  Смена знака неравенства.

Если ограничение задано в виде:

то, умножая её на (- 1), приведем её к виду:

Это справедливо и для обратного преобразования знака.

3) Превращение неравенств в равенства.

Пусть исходная форма задачи линейного программирования имеет вид:

Вводим дополнительные положительные переменные. Получаем:

4) Превращение равенства в систему неравенств.

Если ограничение задано в виде:

,

то его можно заменить эквивалентной системой двух неравенств:

,

или согласно правилу канонического вида:

.

5). Ограничения на неотрицательность переменных.

Во всех приведенных выше формах требуется, чтобы все переменные были

неотрицательны. В реальных задачах часто на переменные накладываются ограничение вида (они называются двусторонними ограничениями), или же условие неотрицательности какой-то переменной может отсутствовать вообще.

Рассмотрим, как поступать в этих случаях.

а) Пусть на переменную вообще не наложено никаких ограничений. Для приведения задачи к канонической форме введем две новые переменные и и будем считать, что

После этого, заменив в исходной задаче на получаем задачу линейного программирования в канонической форме.

б) Пусть на наложено двустороннее ограничение вида .Введем переменную . Тогда будет , что дает ограничения в стандартной форме.

Вводя дополнительную неотрицательную переменную , можно записать двустороннее ограничение в виде:

После того, как в исходных соотношениях вместо будет подставлено выражение и добавлено новое ограничение, задача приобретет канонический вид.

Указанные выше приемы позволяют приводить задачи линейного программирования к стандартной форме, т.е. они взаимообратные.

Пример №1

Дана задача в виде:

при ограничениях:

Привести к каноническому виду задачу:

Переводим max в min, запишем задачу в

Приведем все знаки к одному виду:

Введем дополнительные переменные в систему ограничений

И в целевую функцию

что и дает эквивалентную задачу в канонической форме.

Пример №2

Дана задача в виде:

при ограничениях:

Привести к каноническому виду задачу по аналогии с примером №1:

Получаем задачу:

В канонической форме записи задач линейного программирования все переменные, входящие в систему ограничений, не должны быть отрицательными. Допустим, что

, где

Подставляя данное выражение в систему ограничений и целевую функцию, и записывая переменные в порядке возрастания индекса, получим задачу линейного программирования, представленную в канонической форме: