8.3. Решения игр в смешанных стратегиях

Как мы отмечали выше, если матричная игра содержит седловую точку, то ее решение находится по принципу минимакса. Если же платежная матрица не имеет седловой точки, то применение минимаксных стратегий каждым из игроков показывает, что игрок A обеспечит себе выигрыш не меньше а, а игрок B обеспечит себе проигрыш не больше р. Так как α < β, то игрок А стремится увеличить выигрыш, а игрок В — уменьшить проигрыш. Если информация о действиях противной стороны будет отсутствовать, то игроки будут многократно применять чистые стратегии случайным образом с определенной вероятностью. Такая стратегия в теории игр называется смешанной стратегией. Из сказанного следует, что смешанная стратегия игрока — это полный набор его чистых стратегий при многократном повторении игры в одних и тех же условиях с заданными вероятностями. Для применения смешанных стратегий требуются следующие условия:

1) в игре отсутствует седловая точка;

2) игроками используется случайная смесь чистых стратегий с соответствующими вероятностями;

3) игра многократно повторяется в одних и тех же условиях;

4) при каждом из ходов один игрок не информирован о выборе стратегии другим игроком.

Основная теорема теории игр Дж. фон Неймана: каждая конечная игра имеет по крайней мере одно оптимальное решение в смешанных стратегиях. Следствие: каждая конечная игра имеет цену, являющуюся математическим ожиданием выигрыша игрока А и проигрыша игрока В, причем выигрыш, соответствующий оптимальному решению, называется ценой игры - γ, удовлетворяющий условию α ≤ γ ≤ β. Каждый игрок при многократном повторении игры, придерживаясь смешанных стратегий, получает более выгодный для себя результат. Оптимальное решение игры в смешанных стратегиях обладает следующим свойством: каждый из игроков не заинтересован в отходе от своей оптимальной смешанной стратегии, если его противник применяет оптимальную смешанную стратегию, так как это ему невыгодно.

Чистые стратегии игроков в их оптимальных смешанных стратегиях называются активными.

Обозначим вектор вероятностей (относительных частот) выбора заданных стратегий игрока A следующим образом:

P = (p₁, p₂,…, p_m), i=1…m,

где p_i≥ 0, p₁ + p₂ +…+ p_m= 1. Величина p_i называется вероятностью (относительной частотой) применения стратегии A_i.

Аналогично для игрока B вводится неизвестный вектор вероятностей (относительных частот) имеет вид:

Q = (q₁, q₂,…, q_n), j=1…n,

где q_j≥ 0, q₁ + q₂ +…+ q_n = 1. Величина q_j называется вероятностью (относительной частотой) применения стратегии B_j.

В игре 2x2, не имеющей седловой точки, обе стратегии являются активными.

8.3.1. Решение игры 2×2 в смешанных стратегиях

Покажем на примере платёжной матрицы размерностью 2×2 реализацию алгоритма построения оптимального решения игровой задачи в смешанных стратегиях.

Пример №6

Найти решение матричной игры:

.

Решение:

α= -1, β = 1, α ≠β - решения в чистых стратегиях не существует.

Припишем строкам платёжной матрицы неизвестные вероятности p₁ и p₂ (вероятности выбора стратегий A₁ и A₂) соответственно:

Поскольку p₁ + p₂ =1 , тогда p₂ = 1 - p₁. Обозначим p₁ = p, тогда p₂ =1 - p. В результате получим:

Умножим столбец поэлементно на 1-й столбец и, сложив произведения, получим - математическое ожидание (среднее значение) выигрыша первого игрока A, при условии, что второй игрок B следует первой стратегии:

M₁(p) = 1∙p + (-1)(1-p) = 2p-1

Умножим столбец поэлементно на 2-й столбец и, сложив произведения, получим линейную зависимость - математическое ожидание (средний выигрыш) игрока A при применении игроком B второй стратегии:

M₂(p) = (-1)∙p + 1(1-p) = -2p+1

Поскольку мы разыскиваем оптимальное решение первого игрока A, которое не должно зависеть от выбора стратегий вторым игроком B, приравняем полученные зависимости средних выигрышей:

2p-1 = -2p+1

Отсюда, p= ½, 1-p = ½, то есть оптимальная смешанная стратегия игрока A - это P = (½, ½) (каждую из стратегий надо применять с относительной частотой 1/2). Подставив p= ½, в любую из зависимостей, найдем цену игры:

.

Теперь припишем столбцам вероятности q₁ и q₂ соответственно, а поскольку:

q₁ + q₂ =1 →q₂ = 1 - q₁. Обозначим q₁ = q, тогда q₂ =1 - q. В результате получим:

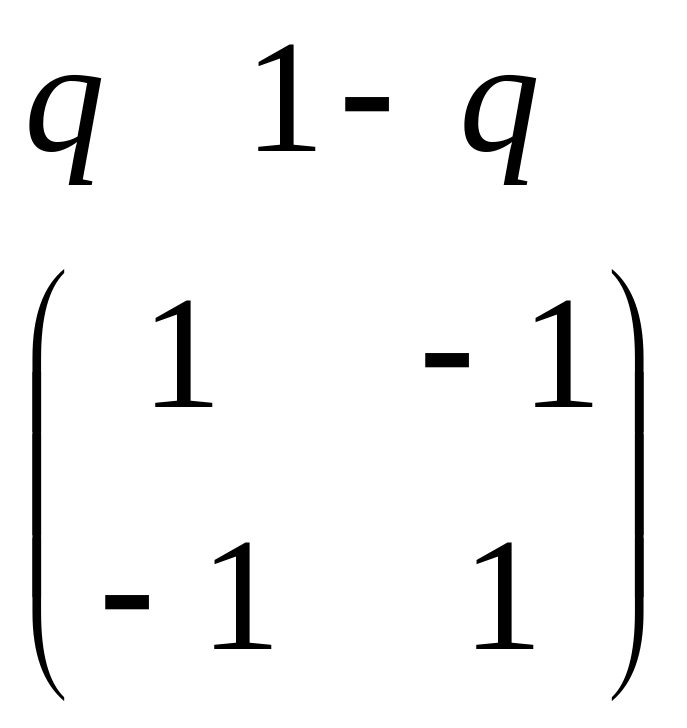
Умножив строку (q, 1-q) на 1-ю строку и сложив произведения, получим линейную зависимость - математическое ожидание:

W₁(q) = 1q + (-1)(1-q) = 2q - 1

Это средний выигрыш игрока A (равный проигрышу игрока B) при применении игроком A 1-й стратегии.

Умножив строку (q, 1-q) на 2-ю строку и сложив произведения, получим линейную зависимость - математическое ожидание:

W₂ = (-1) q + 1· (1-q) = -2q + 1

Это средний выигрыш игрока A (равный проигрышу игрока B) при применении игроком A 2-й стратегии.

Приравняем полученные зависимости:

2q -1 = -2q + 1

Отсюда, q = ½, 1 - q = ½ , то есть оптимальная смешанная стратегия игрока B - это Q = (½;½) (каждую из стратегий надо применять с относительной частотой ½).

Решение о конкретном выборе одной из своих стратегий каждый из игроков может принимать с помощью подбрасывания монеты или бинарного датчика случайных чисел.

Для решения игр в смешанных стратегиях применяют решение с использованием системы уравнений, построенные для игрока А и В. Рассмотрим на примере.

Пример №7

Найти решение матричной игры:

.

Решение:

Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.

Находим гарантированный выигрыш, определяемый нижней ценой игры α = max(α_i) = 4, которая указывает на максимальную чистую стратегию A₁.

 Верхняя цена игры β = min(β_j) = 5, что свидетельствует об отсутствии седловой точки, так как α ≠ β:

Игроки	B1	B2	α
A1	4	5	4
A2	7	3	3
β	7	5

Цена игры находится в пределах 4 ≤ γ ≤ 5.

Находим решение игры в смешанных стратегиях.

 Запишем систему уравнений:

 

Для игрока A в общем случае:

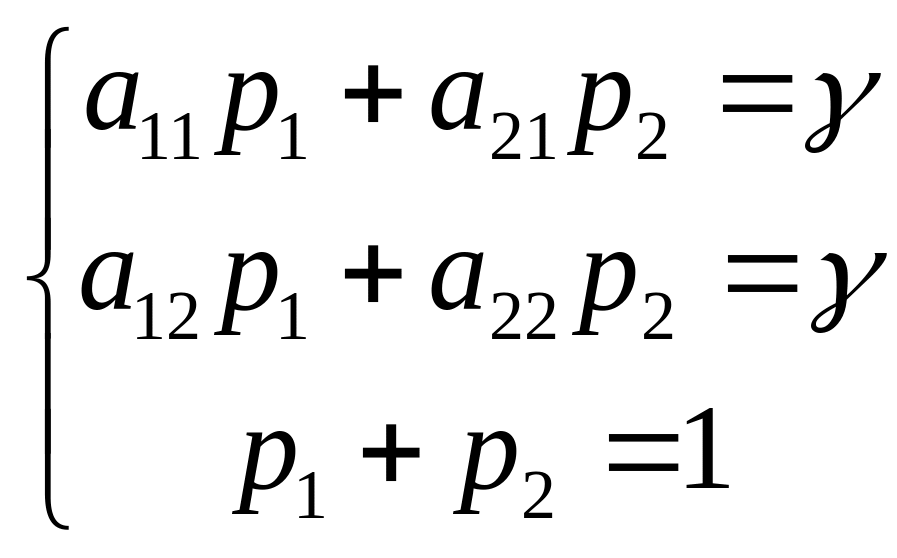
В нашем случае:

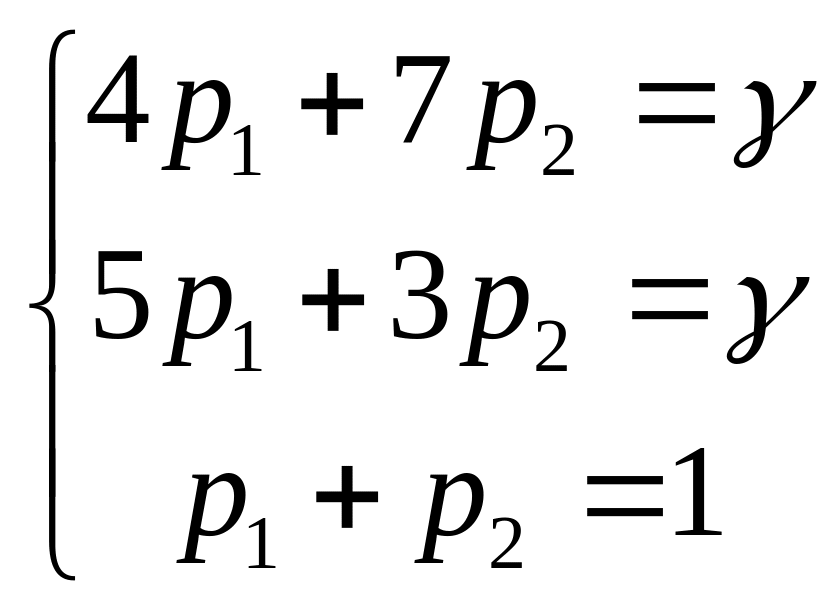
 Для игрока B в общем случае:

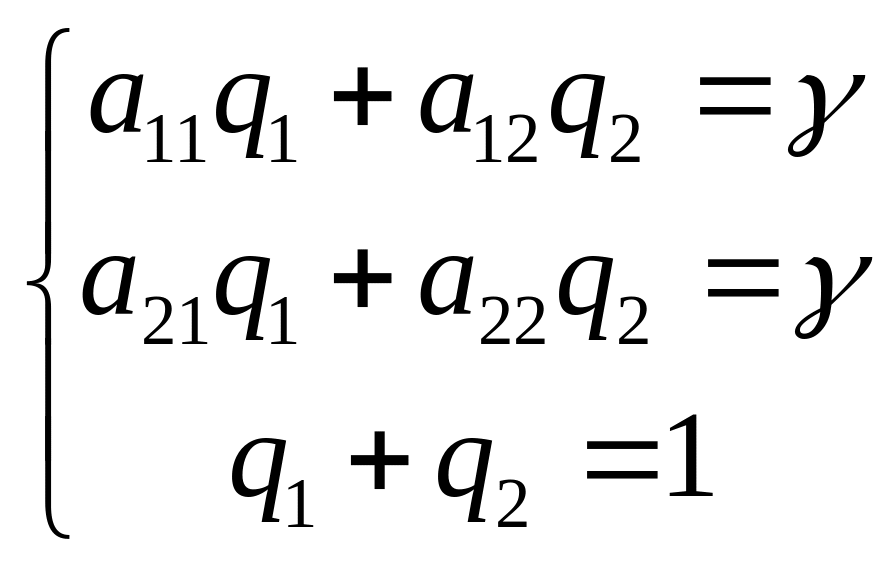
В нашем случае:

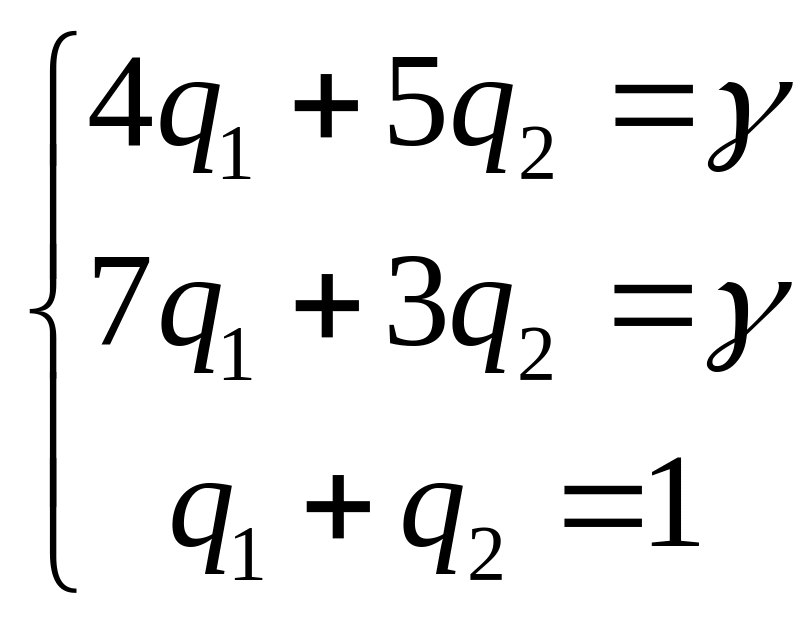
Решая эти системы методом Гаусса, находим:

Получили:

p₁ = ⁴/₅ (вероятность применения 1-ой стратегии).

 p₂ = ¹/₅ (вероятность применения 2-ой стратегии).

 Оптимальная смешанная стратегия игрока А: P* = (⁴/₅; ¹/₅)

 q₁ = ²/₅ (вероятность применения 1-ой стратегии).

 q₂ = ³/₅ (вероятность применения 2-ой стратегии).

 Оптимальная смешанная стратегия игрока В: Q* = (²/₅; ³/₅)

 Цена игры

 γ= 4³/₅ .