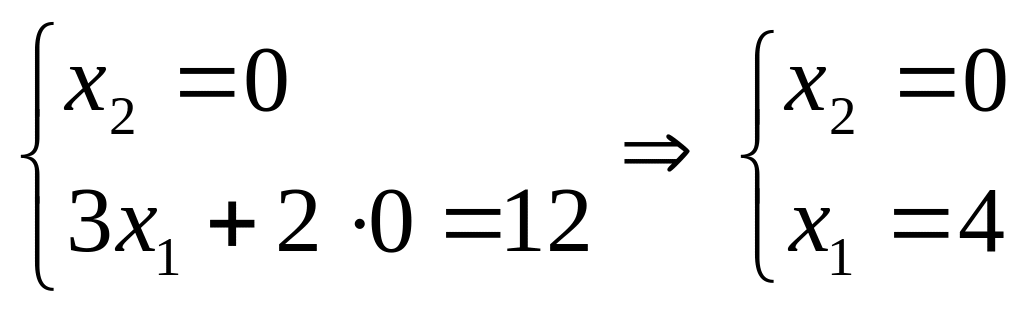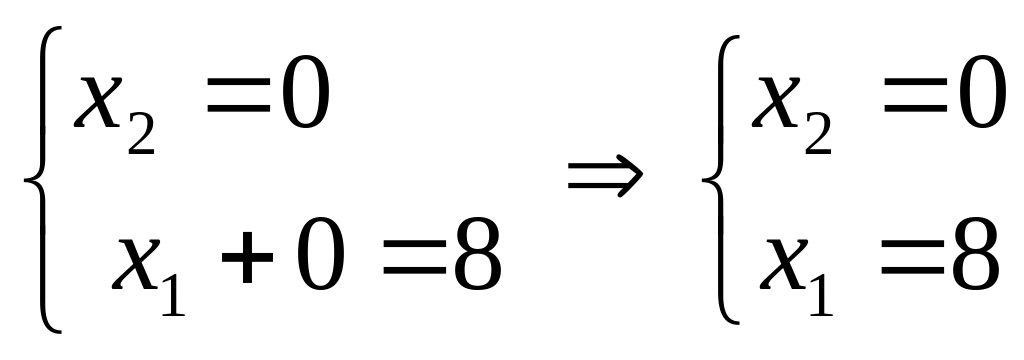1. Изобразим на плоскости систему координат
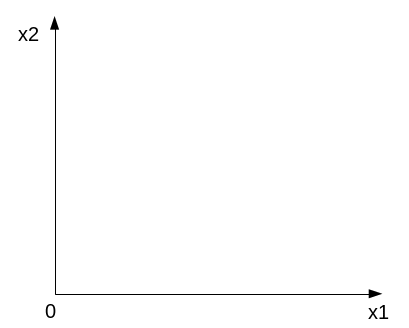
2. Рассмотрим ограничения неотрицательности
а) Неравенство определяет полуплоскость, в которой все точки имеют неотрицательную первую координату
.
б) Неравенству соответствует полуплоскость, где вторая координата каждой точки неотрицательна.
Таким образом, системе неравенств соответствует 1-я четверть.
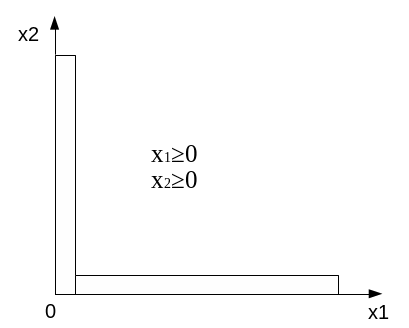
В дальнейшем, если заданы ограничения неотрицательности, все построения проводятся в 1-ой четверти.
3. Строим множество точек, соответствующее множеству решений системы ограничений.
Берем первое неравенство
заменяем его уравнением
Строим прямую, соответствующую этому уравнению.
(Если она не проходит через начало координат, то удобнее всего строить эту прямую по точкам пересечения с осями координат).
С осью 0Х1
|
С осью 0Х2
|
Построенная прямая разбивает плоскость на 2 полуплоскости. Для выбора полуплоскости, соответствующей нашему неравенству, возьмем на плоскости точку с известными координатами, не лежащую на прямой.
Например, возьмем точку М с координатами (8,0).
Подставляем в
неравенство:
.
Получим: 32<24.
Неравенство неверное. Значит, полуплоскость не содержит точки М.
Выберем точку (2,2). Подставим координаты этой точки в неравенство
,
20<24
Получилось верное числовое неравенство. Значит, полуплоскость содержит выбранную для проверки точку.
Таким образом, в совокупности с первой четвертью текущее множество решений представляет собой треугольник ОАВ. Далее аналогично строятся полуплоскости, соответствующие остальным неравенствам, и пересекаются с текущим множеством решении.
2-е неравенство
=>
С осью ОХ1
|
С осью 0Х2
|
Точка для проверки выберем точку 0(0,0)
=>0<12
Верное неравенство.
Полуплоскость содержит точку 0. Пересекаем ее с предыдущим множеством. Получаем четырехугольник 0AMD.
3-е неравенство
=>
С осью 0Х1
|
С осью 0Х2
|
Подставляя в неравенство точку начала координат, убеждаемся, что полуплоскость содержит эту точку.
При пересечении с предыдущим множеством решений и приходим к выводу, что четырехугольник OAMD целиком содержится в данной полуплоскости.
Этот факт свидетельствует о том, что в данной задаче последнее ограничение не существенно и может быть либо отброшено, либо изменено за счет уменьшения запаса ресурса третьего вида.
Окончательно множество решений зачали линейного программирования представляет собой четырехугольник OAMD.
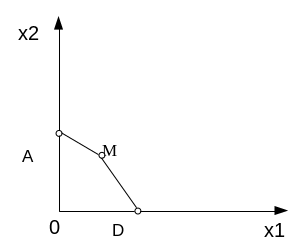
4. Найдем во
множестве решений, точку, которая
доставляет максимум целевой функции
(эта точка будет соответствовать
оптимальному решению).
а) Для этого построим нормальный вектор С=(4,5). Если придать F какое-либо конкретное значение, то прямая N будет проходить перпендикулярно нормали. (При F=0 прямая проходит через начало координат).
б) Перемещая прямую N в направлении нормали, т.к. задача ищем максимальное значение целевой функции. Находим последнюю точку пересечения прямой и множества решений.
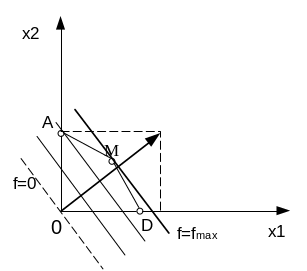
Эта точка и будет искомым оптимальным решением. Определяем ее компоненты как координаты точки пересечения 1-й и 2-й прямых.
Возвращаясь к исходной экономической задаче, можно заключить, что наиболее выгодно производить x1 и x2 в одинаковом количестве.
Пример №2
Решить графически задачу линейного программирования.
при ограничениях:
Решение.
Построим многоугольник решений, для этого проведём граничные прямые:
(1).
|
(2).
|
(3).
|
С помощью контрольной точки 0(0; 0) определим полуплоскости, являющиеся решением соответствующих неравенств. Многоугольником решений является четырехугольник ABCD.
Построим
линию уровня
Вектор
=(3;
-3).
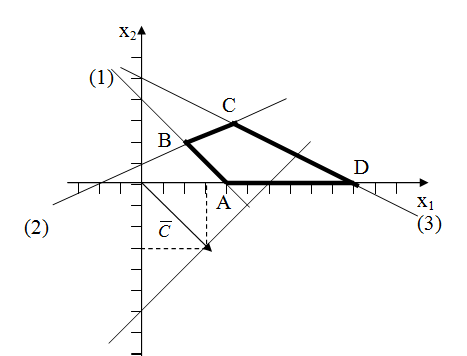
Т. к. в задаче требуется найти минимум целевой функции, будем перемещать линию N в направлении, противоположном вектору градиента. Крайней точкой многоугольника решений, через которую проходит линия уровня, является точка В. Координаты точки В определим, решив систему уравнений (1) и (2), т. к. эта точка является точкой пересечения прямых, задаваемых этими уравнениями.
Тогда
Ответ:
Пример №3
Решить графически задачу линейного программирования.
при ограничениях:
Решение:
Построим многоугольники решений. Проведём граничные прямые
(1).
|
(2).
|
(3).
|
С помощью контрольной точки 0(0; 0) определим полуплоскости, являющиеся решением соответствующих неравенств. Многоугольником решений является четырехугольник ABCD.
Построим линию
уровня
.
Линия уровня с максимальным значением
уровня совпадает с линией, проходящей
через сторону АВ многоугольника решений.
Следовательно, на всём отрезке АВ целевая
функция
принимает одно и то же максимальное
значение, равное
.
Точки отрезка АВ задаются уравнением
,
где
.
Пример №4
Графически также могут быть решены задачи линейного программирования и с большим числом переменных, если их удается свести к ЗЛП с 2-мя переменными и ограничениями-неравенствами.
Например:
Путем отбрасывания
переменных
из системы уравнений, замены их
неравенствами и выражения отбрасываемых
переменных в целевой функции через
переменные
,
задача может быть приведена к виду:
После графического решения (**) переменные определяются из (*).