References

M. Gere, S.P.Timoshenko Mechanics of Materials, 4th edition, Pws Pub Co, 1997.

F. B. Seely, Advanced Mechanics of Materials, John Wiley and Sons, Inc., New York, 1952.

L. Spiegel, G. Limbrunner Applied Statics and Strength of Materials, 3rd edition, Prentice-Hall Career & Technology, 1999.

S. Timoshenko Strength of Materials, Part I & II, Van Nostrand Company, Princeton, N. J., 1956.

THEMES

Theme 1. Stress Concentration Theme 2. Fracure Mechanics Theme 3. Mechanical Properties Theme 4. Strength of Materials Theme 5. Theory of Elasticity Theme 6. Structural Safety Theme 7. Material Science Theme 8. Welds Theme 9.Composite Materials Theme 10. Finite Element Analysis

5. Theory of elasticity

Igor Kokcharov and Igor Zyryanov

5.1 Deformation

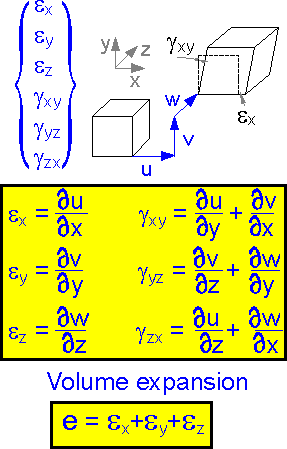An elastic body can be shifted and extended. Analysis of the displacements u, v and w shows whether there is deformation or not. Change of the element sizes and its shape can be characterized by deformation, difference in displacements, or by strain. Strain is the deformation of an element divided by the original length of the element. There are 6 components of strain. There is linear strain ei and shear strain g_ij . The strain e_x is the derivative of displacement u with respect to coordinate x. Definitions for the other strain components are shown in the figure. Volume expansion e depends on linear components of strain only. Shear strain g_xy has no affect on the parameter. 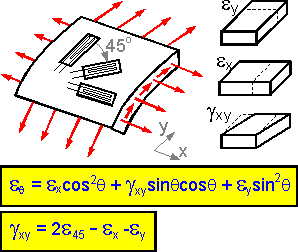The strain components change if the axes is rotated by angle q. According to the second formula shown at the right, shear strain g_xy = 0 if all three linear components of strain are equal. 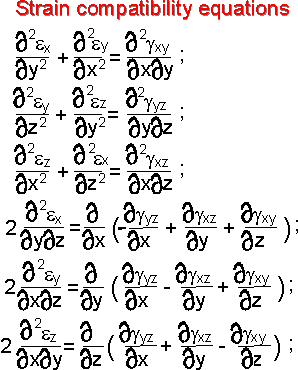In an elastic body strains cannot be chosen arbitrarily, they must satisfy to the strain compatibility equations. 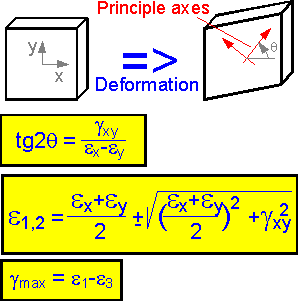For plane strain there are two axes along which the linear strains are at a maximum. The axes are called principle axes. Angle q defines their position. The expressions are given for maximum linear strains e₁, e₂ (plane problem) and maximum shear strain gmax (three-dimensional problem). 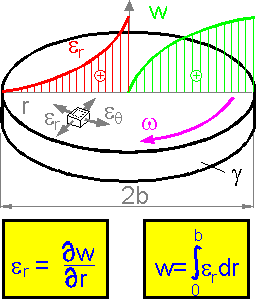The radial displacement w is smaller in the center of rotating disk. The displacement is a result of summation under the shown curve of radial strain e_r. The larger radial strain and gradient of the displacement are observed in the central part of the disk.

5.2 Stress

Stress is the intensity of an internal force acting on a point in an object. Stress is measured in units of force per area. Axial (or normal) stress (s) is defined as the force perpendicular to the cross sectional area of the body divided by the cross sectional area. Shear stress (t) acts parallel to an imaginary plane cut through an object. Centrifugal forces act to move an elementary ring from center. The elementary ring is extended. Both shown stress components, radial and tangential, are positive. 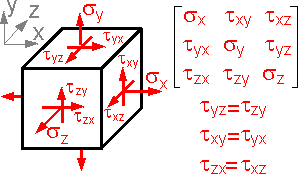There are 9 stress components at any point. The condition for zero rotation of the element, found by taking moments about the axes through the center of the cube parallel to the coordinate axes, reduces the number of independent components to six. Six stress components are enough to describe any state of stress in a point. The equilibrium equations must be satisfied for an elastic body. Mass is not considered in the equations. The shown stress components correspond to three-point bending and satisfy the equilibrium equations. The cut element must be in equilibrium. This requirement helps find the stresses at the incline planes. The sum of the forces at axis x equal to zero. Force is equal to stress * area. The formula gives the expression for principle stresses - normal maximum stresses at incline planes at a point in plane stress state. 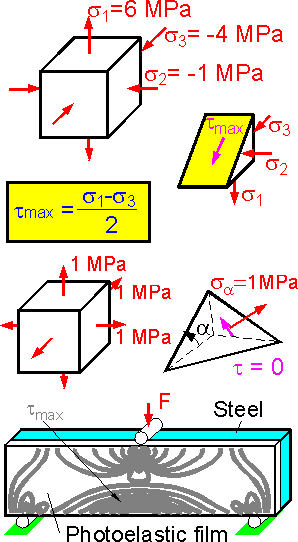The shown normal stresses are principle because there are no shear stresses at the planes. The maximum shear stress acts at an incline plane between maximum and minimum principle stresses s₁ and s₃. Maximum shear stress, t_max = (6-(-4))/2 = 5 MPa. For all around tension where the three principle stresses are equal there is no shear stress at any incline planes. All rectangular coordinate sets can be considered the principle ones. The normal stress at any incline plane is also equal to 1 MPa. The fringe pattern in the photoelastic film shows lines of equal shear stress t_max. Maximum shear stress is equal to one-half the maximum tensile stress. The picture illustrates the regions of high stress (density of the fringes).