5.5 Torsion

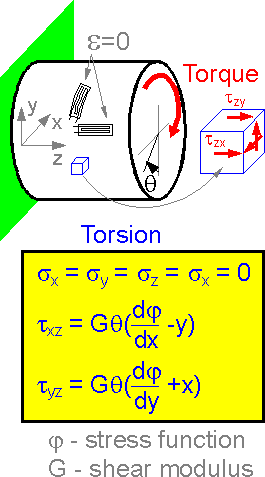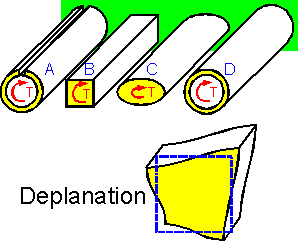
Torsion is related to shear stress. Only two shear stresses are nonzero at planes perpendicular to the shaft axis. All other stress components including all normal stresses in the chosen coordinate axes are equal to zero. There is no tensile strain in the vertical or horizontal directions for pure shear (torsion). There are no readings on the two strain gauges shown. The figure shows the results of a finite element analysis for a prismatic bar under torsion. The shear deformation is at a maximum in the center of the bar. The shape of the square mesh at the surface of the bar changes. The height of the rhombus and its area become smaller. This means that the bar becomes a little shorter. 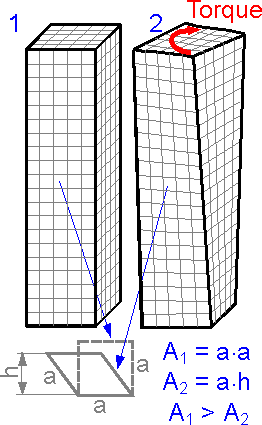The figure shows four specimens with equal cross sections. The thin-walled example A demonstrates the smallest torsional rigidity. The specimens are shown in increasing order of the torsional rigidity. Deplanation of a plane section is the out-of-plane deformation of its points. For all examples except cylinder D there is deplanation. 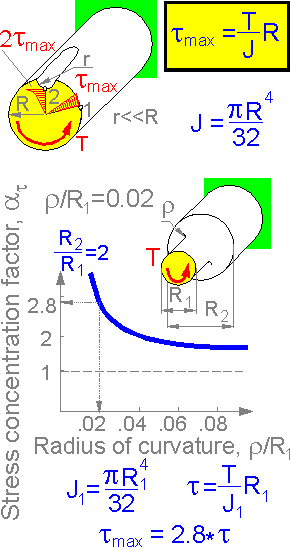Shear stress is doubled near the small keyslot. The stress concentration factor is equal to 2 for the small keyslot. There is stress concentration near the diameter change. The stress concentration factor depends on radius of curvature. 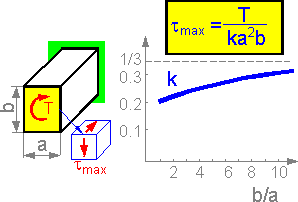The formula defines maximum shear stress for a rectangular section. The maximum shear stress acts at the middle of the longer edge of the rectangle. The coefficient k grows from 0.208 at b/a=1 to 0.333 at infinity. 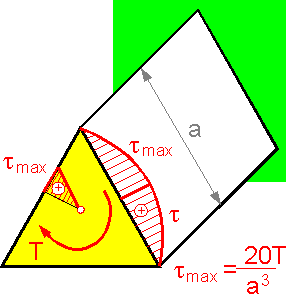Maximum shear stress in the middle of a side of a triangle is inversely proportional to a³. The shear stress is equal to zero in the corners and center. 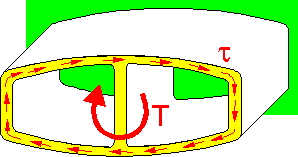For thin-walled symetrical sections the shear stress is approximately zero in the inner wall. All shear stresses tend toward the "external circle".

5.6 Bending

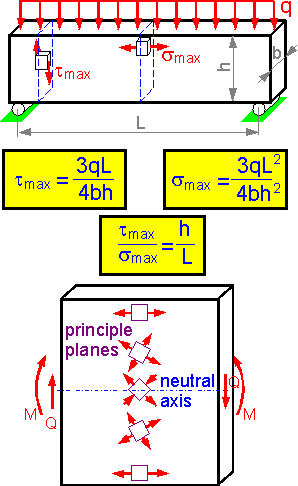There are shear and tensile stresses in bending beams. Usually the beams fail due to bending tensile stress. An exception is beams with high h/L ratio. A height increase results in an increase in the t_max/s_max ratio. The shear stress is at a maximum and there is no tensile bending stress at the neutral line of a bending beam. The maximum tensile stress act at the upper or lower segments of the beam. The principle planes are planes where there are no shear stresses and the normal stresses are at a maximum. The principle axes are inclined by 45^o to the neutral axis. The principle axes coincide with the coordinate axes at the upper and lower sections of a bending beam. The neutral line is shifted to the center for a curved beam. The absolute value of the maximum compressive stress is smaller than that for tension for the shown loading condition. For R/h > 20 the stress field can be considered the same as for a straight beam. 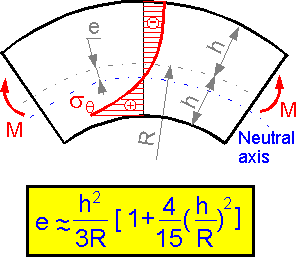The maximum shear stress depends on the transverse force F, the cross-sectional area A and Poisson's ratio m. The shear stress is at a maximum in the center of the section. The bigger the distance from the neutral axis, the bigger the bending tensile stress. 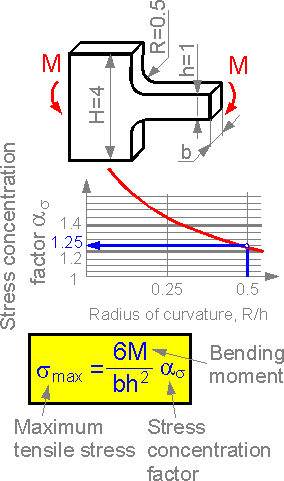There is a stress concentration in the bending beam. The stress concentration factor depends on the ratio of the radius of curvature to the decreased height of the beam. The figure shows a curved central line of the beam. The angle of rotation is at a maximum at the right edge of the beam. 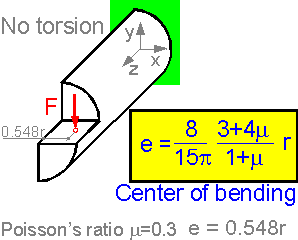Shear stress can result in torsion of non-symmetrical sections. Applying force at a distance e=0.548r does not cause torsion of the beam with a half-round cross section.