
- •Главная
- •1.1 Напряжений и концентраторы
- •1.1.3 Концентраторы напряжения
- •1.3 Stress concentration factor
- •1.7 Elastic-plastic stress concentration
- •1.8 Joints: bolts and welds
- •3. Механические свойства конструкционных материалов
- •3.1 Напряженности испытания
- •3.2 Stress - strain diagram
- •3.3 Testing schemes
- •3.4 Strength
- •4 Прочность материалов
- •4.1 Tension and compression
- •4.2 Shear and torsion
- •4.3 Stress-strain state
- •4.4 Bending: force and moment diagrams
- •4.5 Geometrical characteristics of sections
- •4.6 Bending: stress and deformation
- •4.7 Mixed mode loading
- •4.8 Buckling
- •4.9 Statically indeterminate systems
- •4.10 Three-dimensional structures
- •References
- •5. Theory of elasticity
- •5.1 Deformation
- •5.2 Stress
- •5.3 Hooke's law
- •5.4 Plane problems
- •5.5 Torsion
- •5.6 Bending
- •5.7 Polar coordinates
- •5.8 Plates
- •5.9 Shells
- •5.10 Contact stresses
- •6.2 Distribution functions
- •6.3 Structural models of reliability
- •6.4 Limiting state
- •6.5 Dispersion
- •6.6 Durabilty
- •6.7 Design by reliability criterion
- •6.8 Risk
- •6.9 Safety classes
- •6.10 Risk : structural and social
- •References
- •7 Materials science
- •7.1 Crystalline solids
- •7.2 Mechanical properties
- •7.3 Failure
- •7.4 Phase diagrams
- •7.5 Heat treatment of metals and alloys
- •7.6 Corrosion of metals and alloys
- •7.7 Casting
- •7.8 Polymers
- •7.9 Composites
- •7.10 Forming of metals
- •8.2 Mechanical properties
- •8.3 Stress concentration
- •8.4 Defects
- •8.5 Residual Stress
- •8.6 Strength
- •8.7 Fatigue strength
- •8.8 Fracture
- •8.9 Weldability
- •References
- •9 Composites
- •9.1 Structure of composites
- •9.2 Fibers
- •9.3 Rigidity
- •9.4 Strength
- •9.5 Crack resistance
- •9.6 Optimization
- •9.7 Fatigue and temperature effect
- •9.8 Reliability
- •9.9 Joints
- •9.10 Material selection
- •References
- •10 Finite element analysis
- •10.1 Finite element method
- •10.2 Finite elements
- •10.3 Meshing
- •10.4 Boundary conditions
- •10.5 Deformation
- •10.6 Accuracy
- •10.7 Heat transfer analysis
- •10.8 Dynamics
- •10.9 Computational fluid dynamics
- •10.10 Design analysis
- •References
10.2 Finite elements
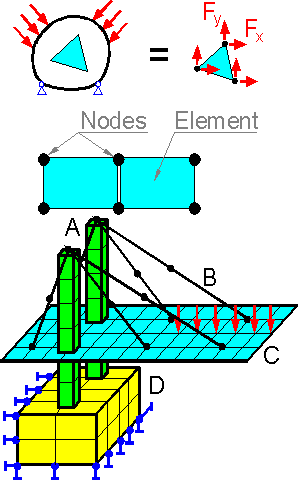 The
mathematical model is subdivided by finite elements which are
connected to each other with nodes. Forces act at the nodes. The
finite element is not a rigid body, the model assumes stresses and
strains exist inside the finite elements.
There are a few
commonly-used finite elements: beam A, truss B, thin shell C, 2D or
3D continuum (D). It is possible to use several types of elements in
one model.
Reliability of the FEA predictions depends on
the number of finite elements. If the inner stresses do not vary
greatly then the number of elements does not have a significant
effect on the accuracy.
The
mathematical model is subdivided by finite elements which are
connected to each other with nodes. Forces act at the nodes. The
finite element is not a rigid body, the model assumes stresses and
strains exist inside the finite elements.
There are a few
commonly-used finite elements: beam A, truss B, thin shell C, 2D or
3D continuum (D). It is possible to use several types of elements in
one model.
Reliability of the FEA predictions depends on
the number of finite elements. If the inner stresses do not vary
greatly then the number of elements does not have a significant
effect on the accuracy.
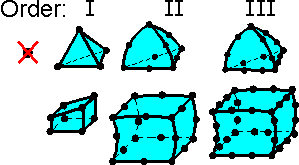 Solid
elements may be linear (first-order elements) or parabolic
(second-order elements). Linear elements have corner nodes only and
their edges are straight. The minimum number of nodes for 3D elements
is 4. Parabolic elements can have a node placed centrally along each
edge and therefore the edges are parabolic. Given the same number of
elements, the higher order elements are more accurate because they
have a more complex mathematical formulation to describe the element
shape (shape function). Also, they represent curved geometry more
accurately. An analysis involving higher order elements requires more
computational resources.
Solid
elements may be linear (first-order elements) or parabolic
(second-order elements). Linear elements have corner nodes only and
their edges are straight. The minimum number of nodes for 3D elements
is 4. Parabolic elements can have a node placed centrally along each
edge and therefore the edges are parabolic. Given the same number of
elements, the higher order elements are more accurate because they
have a more complex mathematical formulation to describe the element
shape (shape function). Also, they represent curved geometry more
accurately. An analysis involving higher order elements requires more
computational resources.
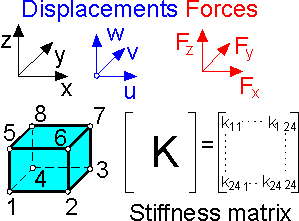 There
are 3 degrees of freedom in a node and 8 nodes for a brick
(hexahedral) element. This means that 24 nodal displacements and 24
nodal forces must be considered. The size of the stiffness matrix
that relates the nodal displacement vector with the nodal forces
vector is [24*24].
There
are 3 degrees of freedom in a node and 8 nodes for a brick
(hexahedral) element. This means that 24 nodal displacements and 24
nodal forces must be considered. The size of the stiffness matrix
that relates the nodal displacement vector with the nodal forces
vector is [24*24].
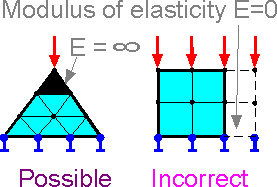 The
stiffness matrix components are inversely proportion to the modulus
of elasticity. Zero modulus of elasticity means that there is no
finite elements. Division by zero modulus of elasticity leads to
numerical errors in the FEM procedures. Infinity modulus of
elasticity means that a part of structure is absolutely rigid.
Although in the theory of elasticity the tensile stress
in the crack tip is equal to infinity, all stresses are finite in
FEM.
The
stiffness matrix components are inversely proportion to the modulus
of elasticity. Zero modulus of elasticity means that there is no
finite elements. Division by zero modulus of elasticity leads to
numerical errors in the FEM procedures. Infinity modulus of
elasticity means that a part of structure is absolutely rigid.
Although in the theory of elasticity the tensile stress
in the crack tip is equal to infinity, all stresses are finite in
FEM.
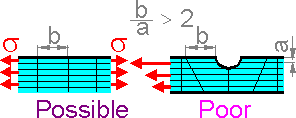 Long
elements can be used if there is not a large gradient of
displacements, strains and stresses. Such elements can be used in
fields of uniform stress but not for stress concentrations. The
stress gradient is high but still finite in zones of stress
concentration.
Long
elements can be used if there is not a large gradient of
displacements, strains and stresses. Such elements can be used in
fields of uniform stress but not for stress concentrations. The
stress gradient is high but still finite in zones of stress
concentration.
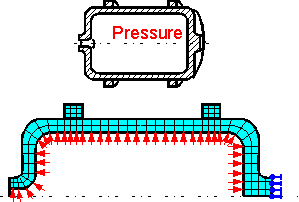 If
a structure and its loads are symmetrical about the axis the problem
can be solved using axisymmetric 2D finite elements.
If
a structure and its loads are symmetrical about the axis the problem
can be solved using axisymmetric 2D finite elements.
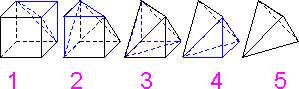 Five
tetrahedral elements are enough to form a cube. Parabolic pyramid
elements provide results that are at least as accurate as linear
brick elements.
Five
tetrahedral elements are enough to form a cube. Parabolic pyramid
elements provide results that are at least as accurate as linear
brick elements.
10.3 Meshing
 A
key step in finite element analysis procedure is to mesh the model.
Meshing is process of breaking the model into small pieces (finite
elements). The network of nodes and elements is called a mesh.
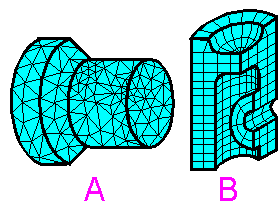
There are two broad types of mesh-generation methods:
structured and unstructured meshes.
A structured mesh B
is formed by grid-based subdividing of the geometry.
Unstructured
mesh are formed automatically. The size of neighboring elements can
be significantly different for unstructured mesh. There are no "rows
and columns" for such mesh, A. There are more nodes than
elements for unstructured mesh with a large number of elements. The
ratio between elements and nodes is approximately 2:1 for 2D
unstructured mesh and 6:1 for 3D unstructured mesh with tetrahedral
elements.
A
key step in finite element analysis procedure is to mesh the model.
Meshing is process of breaking the model into small pieces (finite
elements). The network of nodes and elements is called a mesh.
There are two broad types of mesh-generation methods:
structured and unstructured meshes.
A structured mesh B
is formed by grid-based subdividing of the geometry.
Unstructured
mesh are formed automatically. The size of neighboring elements can
be significantly different for unstructured mesh. There are no "rows
and columns" for such mesh, A. There are more nodes than
elements for unstructured mesh with a large number of elements. The
ratio between elements and nodes is approximately 2:1 for 2D
unstructured mesh and 6:1 for 3D unstructured mesh with tetrahedral
elements.
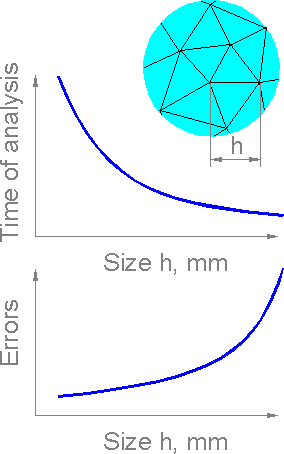 Smaller
mesh size h corresponds to a larger number of finite elements in the
model. The calculation time increases exponentially as size
decreases. The errors decrease for finer mesh but never fall to zero
since FEM is always an numerical approximation.
Smaller
mesh size h corresponds to a larger number of finite elements in the
model. The calculation time increases exponentially as size
decreases. The errors decrease for finer mesh but never fall to zero
since FEM is always an numerical approximation.
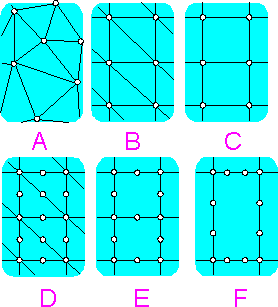 A
linear element requires a finer mesh than a parabolic (quadratic) or
a cubic element.
Structured mesh B is preferable over an
unstructured mesh, A.
Rectangular 4 node elements, C are more
preferable than triangular elements, B.
Quadratic (second order)
triangular elements, D have at least the same accuracy as first order
4 node elements, C.
Rectangular 8 node elements, E are
preferable over triangular second order elements, D despite their
larger size.
Cubic displacement approximation F does not need
fine meshing.
A
linear element requires a finer mesh than a parabolic (quadratic) or
a cubic element.
Structured mesh B is preferable over an
unstructured mesh, A.
Rectangular 4 node elements, C are more
preferable than triangular elements, B.
Quadratic (second order)
triangular elements, D have at least the same accuracy as first order
4 node elements, C.
Rectangular 8 node elements, E are
preferable over triangular second order elements, D despite their
larger size.
Cubic displacement approximation F does not need
fine meshing.
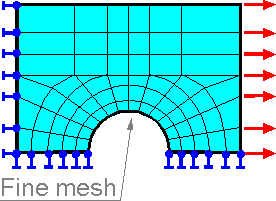 The
FEM is an approximate method. The accuracy of the predictions depends
on the assumptions made within the element types and the mesh. A fine
mesh is required where there are stress and strain gradients (rates
of change). A coarse mesh can be used in areas of reasonably constant
stress or regions that are not of user's interest. Users must be able
to identify regions of stress concentration. Points of interest may
consist of fracture points of previously tested structure, holes,
fillets, corners, contact zones, complex details, and high stress
areas.
The
FEM is an approximate method. The accuracy of the predictions depends
on the assumptions made within the element types and the mesh. A fine
mesh is required where there are stress and strain gradients (rates
of change). A coarse mesh can be used in areas of reasonably constant
stress or regions that are not of user's interest. Users must be able
to identify regions of stress concentration. Points of interest may
consist of fracture points of previously tested structure, holes,
fillets, corners, contact zones, complex details, and high stress
areas.
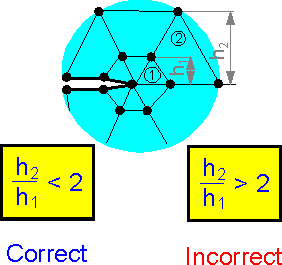 The
accuracy decreases if the sizes of the neighboring elements near
stress concentrators are significantly different.
The
accuracy decreases if the sizes of the neighboring elements near
stress concentrators are significantly different.
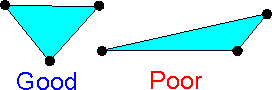 The
shape of finite elements affects the accuracy. It is preferable not
to have sharp corners in finite elements. Elements with similar sides
produce smaller errors.
The
shape of finite elements affects the accuracy. It is preferable not
to have sharp corners in finite elements. Elements with similar sides
produce smaller errors.
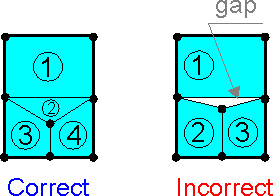 The
FE mesh is built without gaps between elements. Both triangular and
rectangular elements can be used in the same FE model.
The
FE mesh is built without gaps between elements. Both triangular and
rectangular elements can be used in the same FE model.
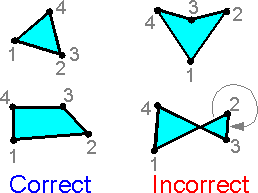 The
nodes are numbered sequentially for manual meshing. It is forbidden
to build four node elements with an obtuse (> 180o)
inner corner.
The
nodes are numbered sequentially for manual meshing. It is forbidden
to build four node elements with an obtuse (> 180o)
inner corner.
