5.7 Polar coordinates

There are tangential s_q and radial s_r stress components in polar coordinates. The coordinates are used for round elastic bodies. The tangential tensile stress is at a maximum at the inner surfaces of a cylindrical tube with inner pressure p_i, A. The tangential stress is negative for external pressure B. There is no stress gradient if the external and inner pressures are equal, C. The eccentricity e increases the maximum tensile stress at inner surface, D. 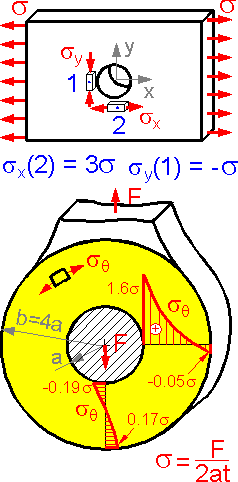There is a stress concentration near the round hole in the plate. The stress concentration factor is equal to the ratio of the maximum to the nominal stress. Stress concentration factor is 3.0 for point 2 . Stress s_y is negative for point 1. Compression is similar to tension, merely change the signs. For the complex loading shown here, the tangential stress sq is at a maximum in the horizontal section due to the effect of "tension + bending + stress concentration". Stress concentration is higher for an elliptical hole under tension than for a round hole. For pure shear the absolute value of normal stress is highest at a point between A and C. For a round hole (a=b) the stress concentration factor is equal to 4 for pure shear. The stress pattern is linear for bending except near the elliptical hole where stress increases. 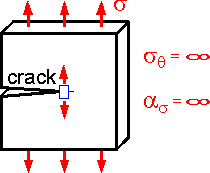The theoretical stress concentration factor for an ideal elastic body is equal to infinity in the crack tip. Infinite stress is not seen in actual materials due to plasticity and finite microstructure. 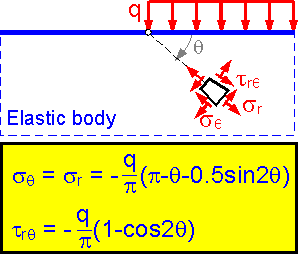The tangential stress is equal to the radial stress for this loading scheme. The stress depends on angle q, not on the radius r. The smaller the angle q, the larger the absolute value s_q. The stress is equal to distributed load q at the surface (q=0). 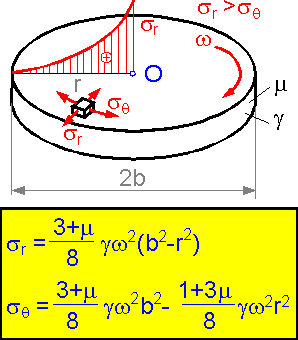A rotating disk: g is the density of material, m is Poisson's ratio, w is the rotation speed. The radial stress is higher than the tangential stress. It is proportional to the squared rotation speed and highest in the center.

5.8 Plates

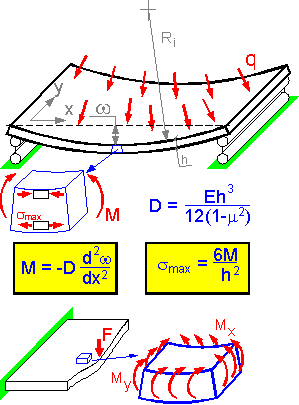Bending is the most important loading situation for thin plates. Bending moment depends on bending rigidity D of the plate and the shape of the deformed plate (deflection and its derivatives). The bigger the thickness h, the bigger the bending rigidity D and the absolute value of the bending moment. Maximum bending stress is proportional to bending moment M and inversely proportional to h³. There is usually bending relative to both axes x and y. For the shown embedded thin plate, upper layers are under compression and lower layers are under tension in the center of the plate. Both normal stress components s_x and s_y are at a maximum at the lower surface of the plate. 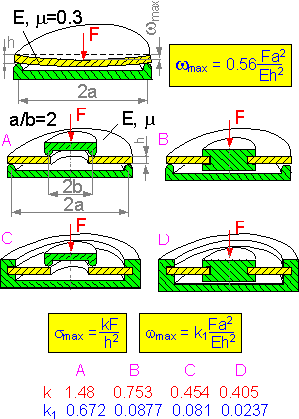The maximum deflection for a round simply supported plate with a force in the center is proportional to (a/h)². The maximum stress and deflection depend on the support method. The more rigid support, the smaller the maximum bending stress s_max and maximum deflection of the round plate. 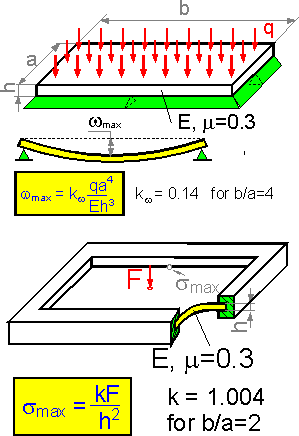The plate shown here is loaded with evenly distributed forces. The maximum deflection in the center the of plate is inversely proportional to h³. Cutting the thickness h in half increases the deflection by 8 times. For a rectangular plate with a force in the center, the bending stress is at a maximum in the middle of the longer side. The stress concentration factor as is smaller for bending of thin plate than for tension of a plate (a_s=3.0). The stress concentration factor for bending depends on Poisson's ratio m. It is approximately equal to 1.8 for steel (m=0.3). 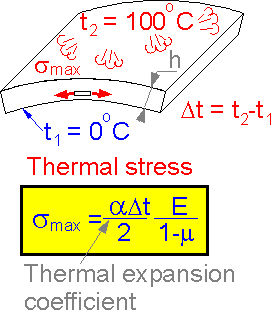The upper surface of the plate was rapidly heated to 100^oC. This causes thermal bending stress in the plate. The thermal stress depends on the difference in temperatures, thermal expansion coefficient and elastic constants of the material. The thermal stress does not depends on the thickness h.