4.3 Stress-strain state

Normal stress in simple tension is given by s=Force/Area. If we cut the section at an angle j, there are two stress components perpendicular (s_n) and parallel (t) to the incline plane. The maximum shear stress occuring at j=45^o is equal to half of maximum axial stress s. 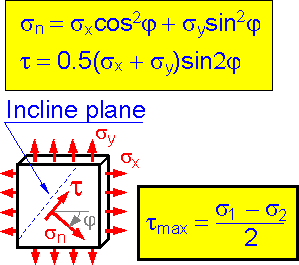For a bi-axial state of stress, normal stress s_n and shear stress t on an inclined plane depend on the two shown stress components. For common plane stress state there are two perpendicular planes (principle planes) where there is no shear stress and normal stresses are a minimum and maximum. The two components are known as the principle stresses. Maximum shear stress acts at the planes inclined 45^o to principle planes. 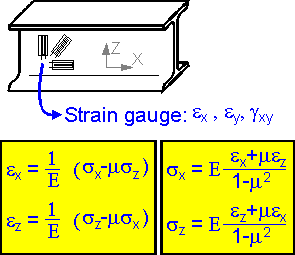Hooke's law generally includes two constants of the material: Young's modulus E and Poisson's ratio m. In the general case, maximum shear stress depends on two principle stresses only - maximum and minimum. 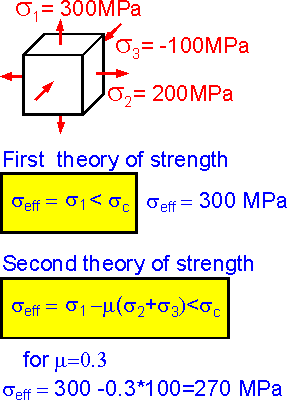According to the first theory of strength fracture occurs if the maximum principle stress exceeds its critical value. According to the second theory of strength fracture occurs if the maximum tensile strain exceeds its critical value. This can be transformed into an equation with the equivalent stress depending on all three stress components and Poisson's ratio.

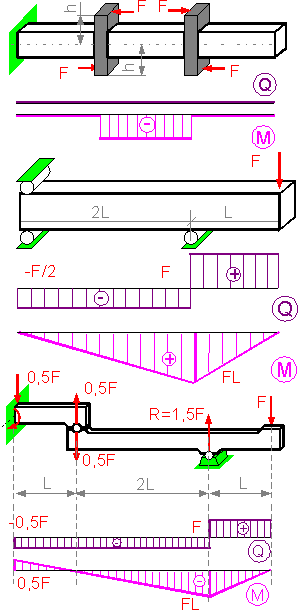
4.4 Bending: force and moment diagrams

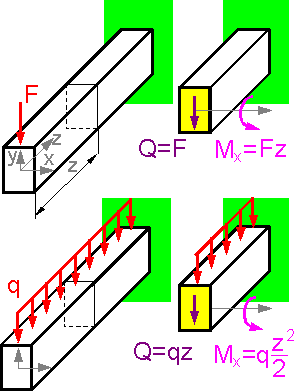A cantilever beam is fully constrained on one end, attached to a wall for example, and has a load acting at the other end.

Static equilibrium conditions

Static equilibrium conditions are applied to determine the external support reactions, and the external moment acting on the beam in the embedded end:

Sum of forces including internal transverse (shear) force Q in Y-direction is equal to zero.

Sum of the moments relative to the chosen point, including internal bending moment M_x, is equal to zero.

The resulting internal bending moment in the beam is proportional to the distance from the free end z. The situation is similar if load is distributed q. The figures show different loading schemes and corresponding diagrams of shear force Q and bending moment M. For the same external load, the support structure can affect the maximum values of the bending moment M.

4.5 Geometrical characteristics of sections

Bending tensile and shear stresses depend on the section geometry, not only the cross-sectional area A. The section can be characterized by the following:

moments of inertia I_xx, I_yy,

polar moment of inertia J.

The last characteristic is important for analysis of torsion deformation. The moments of inertia have units of [length4]. Polar moment of inertia is equal to sum of the other two moments. It does not depend on orientation of the axes. 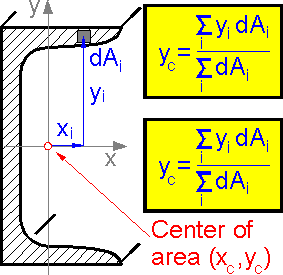The moments of inertia depend on the placement and orientation of the axes. Practical engineers use values of the moments of inertia which pass through the center of the area called the centroid (x_c,y_c). 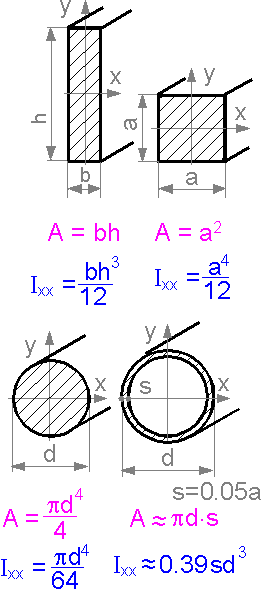For simple geometry the moment of inertia can be easy calculated. For more complicated sections, the information can be found in reference books. The moment of inertia I_xx is higher if many elements of the area are located far from the neutral axis. The removed area of the circle decreases the moment of inertia. The decrease is small if the distance from the neutral axis to the center of the hole is small. 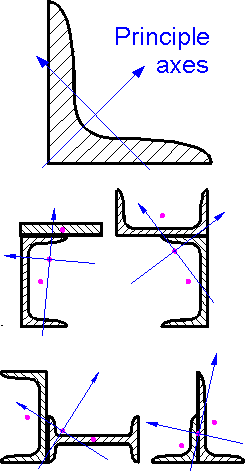For a symmetrical geometry the principle axes pass through the centroid (center of area). An axis coincides with the line of symmetry. For a composite cross-section an axis tends towards the region with most area furthest from the neutral axis.