4 Прочность материалов

4.1 Tension and compression

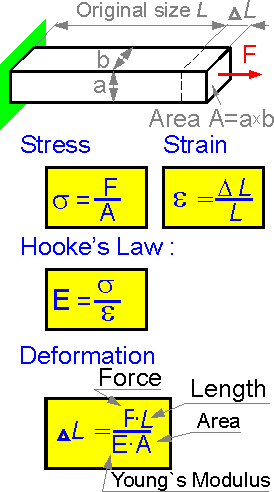Напряженность и сжатие можно охарактеризовать следующими параметрами: деформации, напряжение и стресс. Стресс Стресс - интенсивность внутренних сил. Стресс выражается в силе на единицу площади (мегапаскалях, фунт сила на квадратный дюйм) и негативными для сжатия. Внешние силы причиной деформации членов. Деформации деформации - увеличение в оригинальном размере члена. Он измеряется в единицах длины.

Elongation

Elongation - the increase in gauge length of a body subjected to a tensile force, referenced to a gauge length on the body. The parameter is considered as strain.

Strain

Strain - deformation of member divided by the original length of member. According to Hooke's law for elastic deformation, stress is proportional to strain. The ratio of elastic stress/strain is a constant of the material. This constant is known as Young's modulus or modulus of elasticity. This parameter has units of stress (MPa, GPa). Polyethylene : E = 1 GPa = 1000 MPa Glass : E = 60 GPa = 60 000 MPa Aluminum : E = 73 GPa = 73 000 MPa Steel : E = 207 GPa = 207 000 MPa 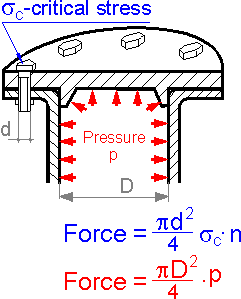For the pressure vessel, the summed force in the bolts is equal to the sum of the force from inner pressures. This condition helps to find the necessary number of bolts n. 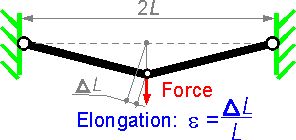Long cables are very flexible, the primary source of deformation in the cables is axial. 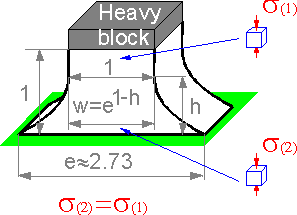There is a compressive stress in the base due to the weight of a heavy block and it's own weight. The figure shows the optimal shape of the base. For such a design, stresses in the bottom and at the top of the base are equal.

4.2 Shear and torsion

Shear stress

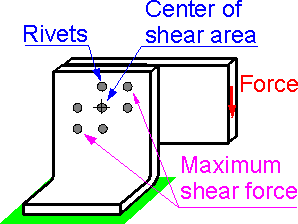Shear stress - the stress component tangential to the plane on which the forces act. Shear stress is expressed in shear force per unit of area (megapascals, pound-force per square inch). Shear stress is highest in the most remote rivet from the center of sum area. There is practically no shear stress in the central rivet. 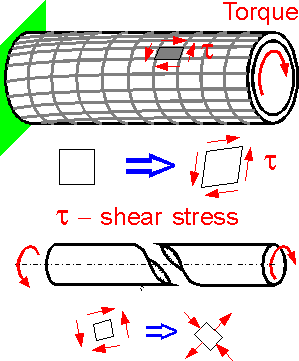Torque transforms a square at the cylinder surface into a rhomb. Absolute values of shear stress at all side surfaces of the rhomb are equal. The stress state of pure shear is equivalent to bi-axial tension-compression state. Tensile stress can result in the brittle fracture of shafts under torsion. The figure shows typical failure of a cylindrical shaft made from brittle material. 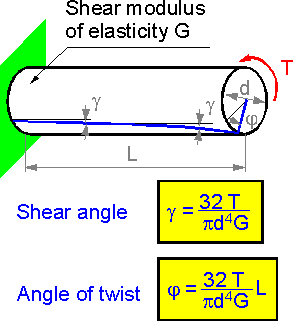There are two angles that help to describe torsion: shear angle g and angle of twist j. The shear angle does not depend on the length of a shaft with constant torque. The longer the shaft, the bigger the angle of twist. 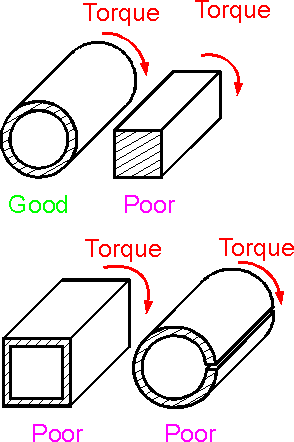A cross section without a sharp corner corresponds to uniform shear stress and effective use of the material. Rigidity depends on polar moment of inertia J which is proportional to r⁴. The bigger the radius r, the bigger the rigidity. Rigidity of an open thin-walled shell is sufficiently smaller than rigidity of a closed section.

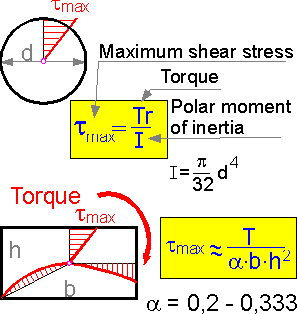
Torsional stress

Torsional stress - the shear stress on a transverse cross section resulting from a twisting action. Torsional stress is at a maximum at the surface. It is equal to zero in the center. The stress is proportional to the applied torque. For a rectangular cross section the maximum shear stress acts along the longer side, closest to the center point. 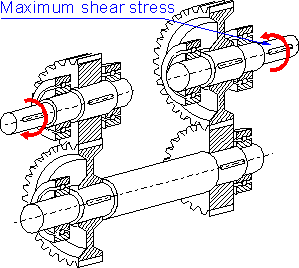Shear stress is at a maximum for the shaft with the highest torque. The moment is the highest for the shaft with lowest rotation speed - the last shaft in the kinematic chain.