10.10 Design analysis

FEA is used to optimize design, guarantee safety, reduce design-cycle time, weight, costs, and the need for testing. Practitioners can use FEA - to prove design safety; - to meet code requirements; - to modify an existing design; - to test new and competing designs; - to peer inside design and see phenomenon that cannot be measured with experimental methods. 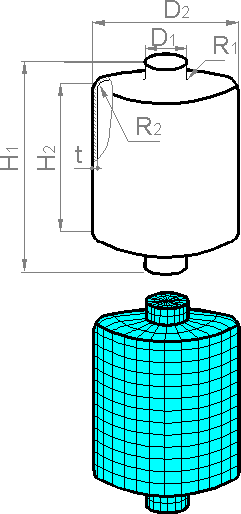Now FEA packages are integrated with solid modeling and computer aided design (CAD) systems. CAD is the use of geometric or solid modeling programs to aid in the creation or modification of a design. A structure may be drawn in solid model form by one of the many CAD packages available. Wireframe is a geometric representation of 3D model as outlined by its outer edges. The model is transferred to a FE software, where it is meshed and boundary conditions are specified. The stresses, displacements, temperatures and other parameters are results of the FE solution. The results help to make decisions on changes in structure design, loads or service regimes. CAD and FEA are becoming integrated. A FEA analysis is not simply translating a CAD file and watching the results. Considerable care and skill has to be employed to be sure that the results correspond to the reality and all scenarios are taken into account. 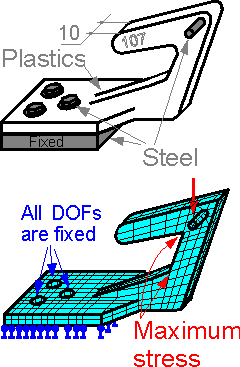Transferring a model from a CAD system assumes some simplification of the model. The fillets in the area of maximum stress concentration are the subject of detailed analysis. 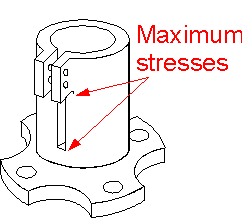Fillets are not always modeled in detail. If the calculated maximum stress is large then one of the possible ways to guarantee the safety of the new structure is in correct design of fillets which can decrease stress concentrations. 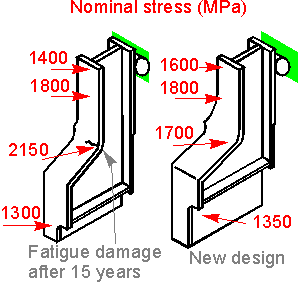FEA is also used to calculate nominal stresses in different regions of the structure. The FEA can be useful in comparing of old and new designs with similar manufacturing technologies. If nominal stresses in the model of a new design are smaller than for the old the conclusion of the analysis is the new design is at least as safe as the old one. 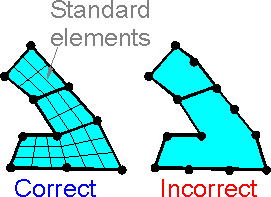There are about 100 types of standard finite elements in commercial FE packages. Automatic meshing procedures can divide the sub-areas on standard elements. There are no plane elements with 5 or 11 nodes. The number of nodes in a finite element cannot be chosen arbitrary.

FEA solves problems using

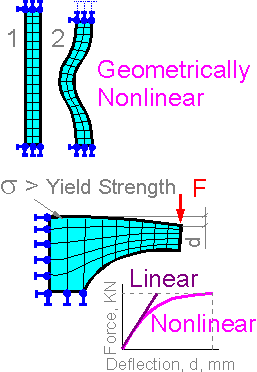Stress Analysis Stresses, displacements, deflections are calculated for static loading. Steady-state or Transient Heat Transfer Predicting temperature distribution for an object exposed to heating, radiation, convection and conduction. Thermal Stress Analysis Stresses and displacement due to thermal expansion are a subject of the analysis. Transient Dynamic Objects in rapid motion or under impact are studied to obtain maximum stresses, deflection. Dynamic incremental nonlinear analysis assumes not one, but many solution steps for nonlinear system. Time for solution of the problem is significantly higher than for static analysis problem. Modal Analysis Vibration characteristics such as natural frequencies and mode shapes are calculated. Fluid Flow Fluid flow in gases, air, and water is modeled to find temperatures, pressures, velocities, etc. Linear Buckling Calculates the load at which a structure is likely to fail due to elastic instability. Non Linear Analysis Analysis for large deflections and nonlinear material behavior such as plastic. 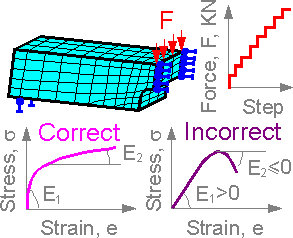Nonlinear problems are solved by with step-by-step increments of applied loads F. At each step the material constant (effective modulus of elasticity) changes depending on the level of stress intensity in the FE for a previous step and material behavior ('stress-strain' diagram). At each loading step the components of the stiffness matrix change according to the new level of stress. It is better to avoid infinitely large or negative diagonal components of the stiffness matrix. This can lead to numerical "oscillation" and errors in the analysis.