10.8 Dynamics

Modal Analysis. Understanding the natural frequencies and corresponding modes of engineering structures can help improve performance and guarantee safety. Changing the external forces causes dynamic effects. For example, vibrations are generated in vehicles from motors or road conditions, in ships from waves, in airplane wings due to turbulence, etc. The maximum stresses resulting from the vibration are considered in engineering analysis. The stresses define the lifetime of a stru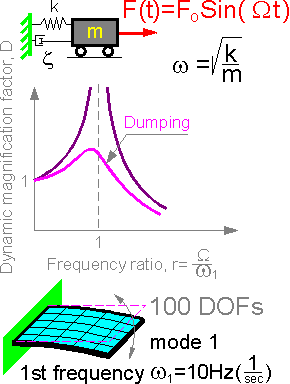cture. Vibration involves repetitive motion. Frequency is defined as the number of cycles in a given time period. 10 Hertz is the same as 10 cycles per second. The dynamic magnification factor D is equal to the ratio of amplitude at a given frequency to amplitude of the static response. The number of characteristic frequencies of the model is equal to number of DOF in the FE model. The most important results are within the first few natural frequencies. The coincidence of the external vibration with the first (and smallest) fundamental frequency results in the maximum deflection of the structure. The first frequency is a property of structure. It does not change if the number of FE in the model increases. FEM solves the eigenvalue problem with better approximation for low frequencies. The higher the frequency, the smaller the correspondence between the FE model and the real situation. There is no need to predict all high frequencies for a structure. It is possible to identify one structure from another by the set of natural frequencies, the "finger prints" of a structure. The most serious consequences occur when a power-driven device produces a frequency at which an attached structure naturally vibrates. This effect is called "resonance". If sufficient power is applied, the structure can be destroyed. The major purpose of the modal analysis is to avoid resonance. Ideally, the first mode must have a frequency higher than any potential driving frequencies. 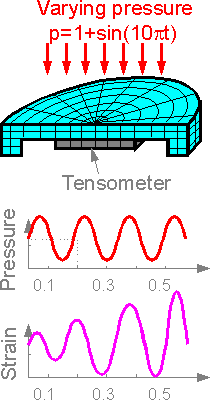In the example, the membrane of a load cell is compressed with variable external pressure. External pressure is applied to the membrane with a frequency of 1 / (time period) = 1 / 0.2 = 5 Hz. If the FEA shows that the natural frequency of the membrane is about 5 Hz resonance will take place. The load cell cannot correctly reflect the pressure values. It is recommended to use the cell with lower frequency external pressure. If this is not possible then the cell design must be changed. An increase of the modulus of elasticity E can increase the fundamental frequency w₁. Natural frequency decreases for heavier material. The following linear eigenvalue problem is solved to calculate the natural frequencies and associated mode shape of a finite element model. Here [K] is the structural stiffness matrix; [M] is the mass matrix; w_i is the i^th natural frequency; {D_i} is the i^th mode shape or eigenvector. Natural frequencies and mode shapes are the results of modal analysis. They do not depend on static loading schemes. The force vector is a zero-element vector. Predicting the effects of impacts are the most common use of transient dynamics. The second formula given shows the dependence of dynamic response on applied force. Stiffness matrix relates forces and displacements. Inertia is described by point accelerations. Damping effect is defined by the velocity of the body. Analysis of dynamic response by FEM is shown in the example. The solutions were obtained for a time interval Dt. The smaller the time interval the smaller the errors. There is a critical value Dt_critical above which the step-by-step integration leads to significant error. The value of Dt_critical depends on the highest frequency of the model. 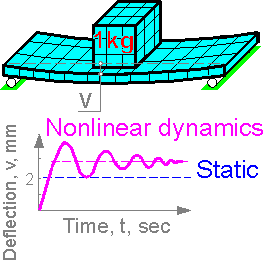In the example a static load had caused tensile stress to reach the yield strength in the low-carbon steel thin plate. The dynamic response problem of the weight dropped onto the plate from a height of 0.5 meter is solved with nonlinear dynamic analysis. There are damping vibrations. The dynamic magnification factor is much larger than 1. This means that at dynamic loading the stress exceeds the yield strength of the material and there is a residual deformation in plate that is larger than the static one.