10.6 Accuracy

Numerical modeling requires approximations and simplifications. The results of FEA are not error-free. Using such a powerful tool as a "black box" without proper understanding of the its principal features can lead users into serious mistakes. Unfortunately human error is inevitable. An design engineer must understand: - Which FE analysis is appropriate for an engineering problem; - What part of the structure must be studied in detail; missing value Formulation errors take place if the finite elements do not precisely describe the behavior of the physical problem. Selecting the proper element type and mesh size will reduce formulation errors. Formulation of boundary conditions is critical for the analysis. The success of FEA depends on the how closely the boundary conditions, geometry, and material behavior of the model match the actual situation. FEM's approximation of a real engineering structure with a finite number of finite elements, as well as the size and shape of the elements can cause discretization error. Numerical errors are usually rare in comparison with the discretization and formulation errors. 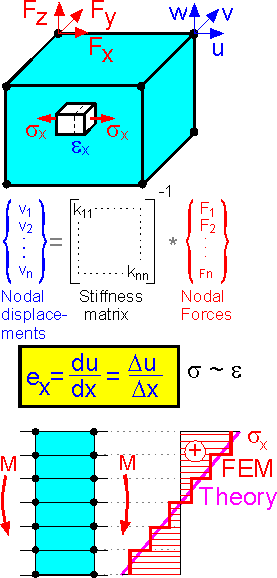Displacements are the primary unknowns. The FEM solution is usually obtained as a vector of nodal displacement {v}. The solution at other locations throughout the element is generally calculated by interpolation. After approximating the displacement field with shape functions the strain and stress can be calculated. This means that accuracy is at a maximum for nodal displacements. Strain is calculated by determining the difference in displacement between corresponding points. This is why the accuracy for strain and stress is at a maximum in the central part of the finite elements. The figure shows a stress pattern for bending. The theoretical and numerical solutions coincide at the center point of the elements. The type and number of finite elements affect the accuracy of the modeling. For the nonlinear analysis where force is calculated the number of elements in the model affects the value of the force for small numbers only. The force becomes more stable with an increase in the number of elements. 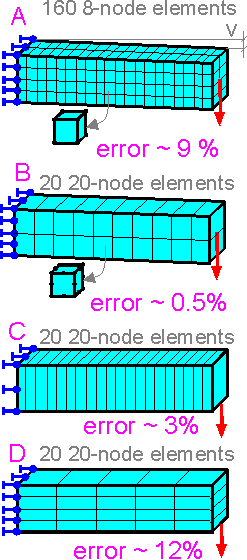The are two methods to increase the accuracy for the solution shown: H-method increases the number of elements, h is the length of one side of an element. P-method increase the polynomial order of the element. Second-order elements, B demonstrate the higher accuracy. For bending of the cantilever beam one element over the height of the beam is not the best choice. The more parabolic elements in the length, the better. 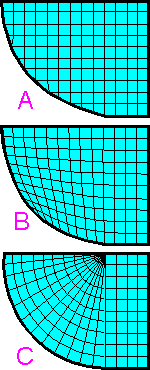Mesh A is preferred for the problem of computational fluid dynamics (CFD). A. Structured rectangular mesh. Numerical approximations are centered about the centroid of the rectangle element. B. Structured deformed mesh. There are many elements where numerical approximations are not centered (or symmetrical). C. Block-structured mesh. Elements are condensed at one point along the straight border. 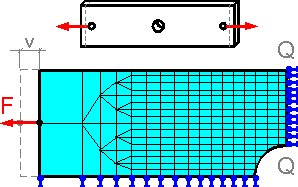Nonlinear structural analysis predicts the behavior of the mild steel specimen. The coarse mesh at the left end does not have a significant effect on results for the region with the finer mesh such as the value of maximum stress, the strain pattern in the net section Q-Q, or deformed shape of the central hole. The condition of force applied on the left side of the model roughly agrees with the real situation. The errors in the numerical diagram "Force - Displacement F-v" are possible due to the coarse mesh at the left end of the model. Errors due to numerical analysis increases if small values of volumetric strain e_V is multiplied by large values of the bulk modulus K. Such analysis requires additional tests. The situation occurs when Poisson's ratio approaches a value of 0.5.