10.4 Boundary conditions

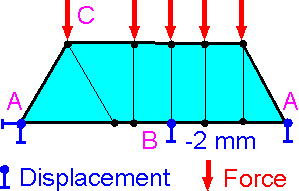Application of boundary conditions is the most critical stage of the finite element analysis. To simulate the constraints imposed on the physical motion of the structure, displacement boundary conditions A, B must be defined. Prescribed displacements can have zero A or non-zero B values. There are also load boundary conditions, C. 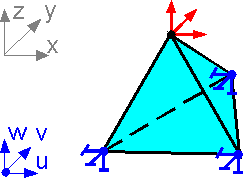The boundary conditions (fixation or force for a direction) are applied at the nodes only. Maximum number of boundary conditions for a node is equal to the degrees of freedom: 3 restraints or forces for a node in this example. 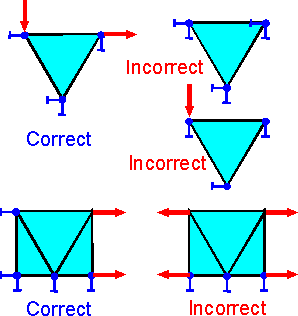Great care must be taken so that the finite element model is neither under constrained nor over-constrained. It is not possible to fix all degrees of freedom (all nodal displacements) for an element. It is better to remove the element from the model. It is not possible to fix a node and to apply force in the same direction. Absence of restraints along an axis can lead to a shift along the axis due to errors in numerical calculations. The correct boundary conditions must have at least one restraint for each axis. 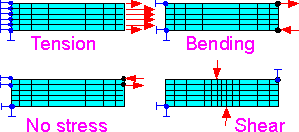Different sets of load and displacement boundary conditions can be implemented to represent model tension, pure bending or shear. 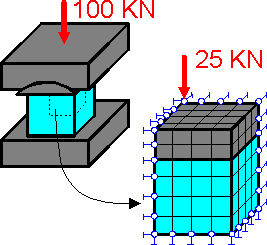There are three planes of symmetry in this example. If the cube is more flexible than the platens then there is no need to model the entire structure. All points of the upper cube surface will have virtually the same vertical displacements.

St Venants principle:

Two sets of statically equivalent forces produce the same stress field at distance that is large compared to linear dimensions of cross section: b > a.

This principle is often utilized to replace complex boundary conditions with statically equivalent loads. The figure shows two equivalent loading schemes. Tensile stresses are frequently the reason for failure in a structure. If the region of maximum tensile stress extends beyond the region of the applied force it is not necessary to have a very fine mesh in that region. There are compressive stresses in region of applied force. This is an example how the distributed load are spread over the nodes. The sum of the force is equal to 18 kg for a half of the plate. The force can be distributed as the weight over 6 nodes.

10.5 Deformation

Most finite element procedures are based on the "displacement method". From the law of equilibrium, the sum of the forces (internal and external) on a node must equal zero. The unknown variables are the displacements. The following is the matrix form of the equilibrium equations:

[K] {D} = {F}

[K] = global stiffness matrix; {D}= displacement vector; {F} = load vector. The stiffness matrix [K] is symmetrical about the diagonal. There are two main types of solvers: direct and iterative. Direct solvers are usually based on Gaussian elimination technique. The direct solvers are more robust but can be slow and require large amounts of disk space for very large problems. Iterative solvers can be extremely fast and require small disk space. The matrix equation is solved for the displacement vector {D}. Strains can be computed from the displacement results. The figure shows how the strain depends on the nodal displacements. There is a shift along axis x by 5mm : e_x = 0. Displacement v increases along axis y: e_y is positive. 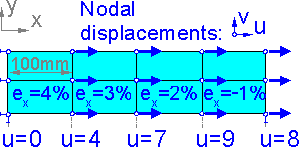For first order elements the tensile strain is defined by the difference between corresponding displacements. There is a linear function for displacements inside the 4-node element. This means that the maximum displacement is only in nodes. The strain is constant for the element. The strain function is quadratic for the second order element shown. The post-processor visualizes the static or animated description of the deformed shape. The deformed shape of the structure is obtained by summing the nodal coordinates and the nodal displacements multiplied by factor k. The deformed shape helps us to understand many things about the structure such as the position of a region under deflection, where maximum distortion takes place, the accuracy of the applied restraints, and other features of the structural deformation. The figure shows the initial and deformed shape of a thin plate. The magnification factor is k=1. It is possible to obtain large deformation even if the material properties remains linear (elastic). The problem was solved by a (geometrically) nonlinear structural procedure. The step-by-step loading solution is implemented in this case. The low bending rigidity assists in large linear deformation. The bending rigidity is low if the elastic modulus or thickness t are small. Theoretically, the size of the finite elements do not effect rigidity. The deformed shape can help the user to decide if the boundary conditions are properly prescribed. No rotations is allowed at edges 1 and 2, only 1 rotation componet at edges 3 and 4. All displacements are linear for these four-nodes plane elements. There are no gaps between the finite elements. The edges can be polygonal lines if the number of finite elements in the model is large. 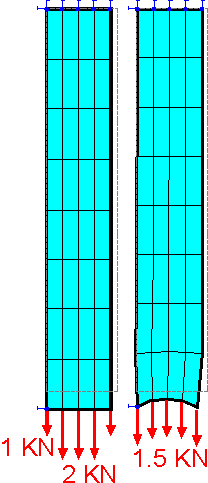This figure shows the deformed shapes for different loading schemes. The uniform stress and deformation fields can be obtained for the second loading scheme. It is better if the loads at the edges are half of those in the center. 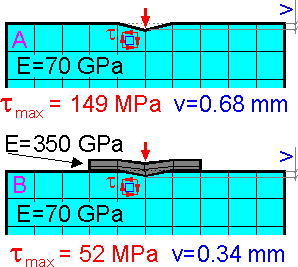The maximum deformation is in the point where the force is applied. The maximum shear stress in the body occurs in the surface element under the force. The rigid plate redistributes force in the body. The contact stress in the body is smaller for the second example. The calculated value of maximum shear stress depends on the size of the elements. 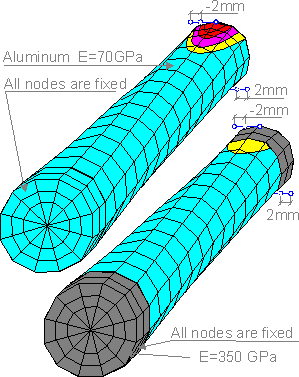The left end of the shaft is fixed in all nodes. Two nodes on the opposite end are shifted by 2 mm. This loading situation corresponds to torsion. There is a stress irregularity at the right end. If the ends of the shaft are made of relatively rigid material, the local deformation will be distributed over the entire shaft. The stress field is more homogeneous for the second instance.