
- •Главная
- •1.1 Напряжений и концентраторы
- •1.1.3 Концентраторы напряжения
- •1.3 Stress concentration factor
- •1.7 Elastic-plastic stress concentration
- •1.8 Joints: bolts and welds
- •3. Механические свойства конструкционных материалов
- •3.1 Напряженности испытания
- •3.2 Stress - strain diagram
- •3.3 Testing schemes
- •3.4 Strength
- •4 Прочность материалов
- •4.1 Tension and compression
- •4.2 Shear and torsion
- •4.3 Stress-strain state
- •4.4 Bending: force and moment diagrams
- •4.5 Geometrical characteristics of sections
- •4.6 Bending: stress and deformation
- •4.7 Mixed mode loading
- •4.8 Buckling
- •4.9 Statically indeterminate systems
- •4.10 Three-dimensional structures
- •References
- •5. Theory of elasticity
- •5.1 Deformation
- •5.2 Stress
- •5.3 Hooke's law
- •5.4 Plane problems
- •5.5 Torsion
- •5.6 Bending
- •5.7 Polar coordinates
- •5.8 Plates
- •5.9 Shells
- •5.10 Contact stresses
- •6.2 Distribution functions
- •6.3 Structural models of reliability
- •6.4 Limiting state
- •6.5 Dispersion
- •6.6 Durabilty
- •6.7 Design by reliability criterion
- •6.8 Risk
- •6.9 Safety classes
- •6.10 Risk : structural and social
- •References
- •7 Materials science
- •7.1 Crystalline solids
- •7.2 Mechanical properties
- •7.3 Failure
- •7.4 Phase diagrams
- •7.5 Heat treatment of metals and alloys
- •7.6 Corrosion of metals and alloys
- •7.7 Casting
- •7.8 Polymers
- •7.9 Composites
- •7.10 Forming of metals
- •8.2 Mechanical properties
- •8.3 Stress concentration
- •8.4 Defects
- •8.5 Residual Stress
- •8.6 Strength
- •8.7 Fatigue strength
- •8.8 Fracture
- •8.9 Weldability
- •References
- •9 Composites
- •9.1 Structure of composites
- •9.2 Fibers
- •9.3 Rigidity
- •9.4 Strength
- •9.5 Crack resistance
- •9.6 Optimization
- •9.7 Fatigue and temperature effect
- •9.8 Reliability
- •9.9 Joints
- •9.10 Material selection
- •References
- •10 Finite element analysis
- •10.1 Finite element method
- •10.2 Finite elements
- •10.3 Meshing
- •10.4 Boundary conditions
- •10.5 Deformation
- •10.6 Accuracy
- •10.7 Heat transfer analysis
- •10.8 Dynamics
- •10.9 Computational fluid dynamics
- •10.10 Design analysis
- •References
9.2 Fibers
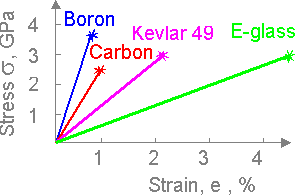 Fibers
demonstrate unique mechanical properties: modulus of elasticity and
strength.
The critical force for a fiber is equal to the
production of critical stress (strength) by the fiber area.
Knotted
aramid fiber keeps up to 50% of its original strength. Other fibrous
material are more brittle.
There is small effect of temperature
and deformation rate on strength of brittle fibers such as boron or
SiC.
Fibers
demonstrate unique mechanical properties: modulus of elasticity and
strength.
The critical force for a fiber is equal to the
production of critical stress (strength) by the fiber area.
Knotted
aramid fiber keeps up to 50% of its original strength. Other fibrous
material are more brittle.
There is small effect of temperature
and deformation rate on strength of brittle fibers such as boron or
SiC.
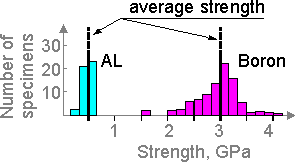 Fibers
differ from other structural materials due to a larger scatter in
experimental data.
Fibers
differ from other structural materials due to a larger scatter in
experimental data.
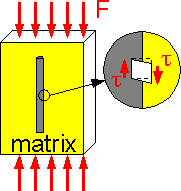 Shear
stress causes fracture of the fiber-matrix bond.
Usually
fibers are round. Larger bond surfaces between matrix and fiber
corresponds to higher crack resistance of a composite
material.
Shear
stress causes fracture of the fiber-matrix bond.
Usually
fibers are round. Larger bond surfaces between matrix and fiber
corresponds to higher crack resistance of a composite
material.
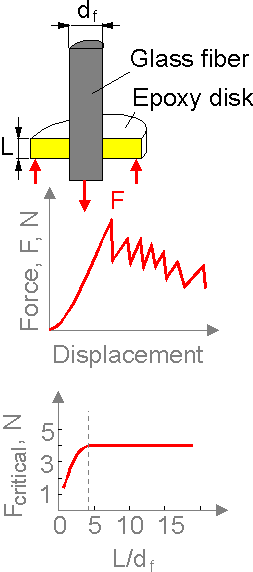 Effect
of friction between matrix and fiber after bond fracture is reflected
in a В«force-displacementВ»
diagram. Critical forces depend on bond length for small L only.
Effect
of friction between matrix and fiber after bond fracture is reflected
in a В«force-displacementВ»
diagram. Critical forces depend on bond length for small L only.
9.3 Rigidity
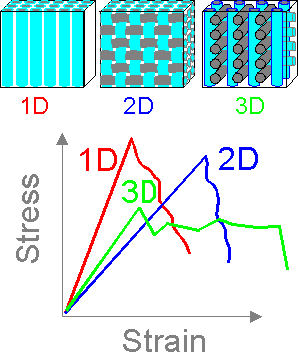 Modulus
of elasticity (Young's modulus) is a measure of rigidity. Modulus of
elasticity has units of stress - [GPa] or [MPa].
Modulus
of elasticity (Young's modulus) is a measure of rigidity. Modulus of
elasticity has units of stress - [GPa] or [MPa].
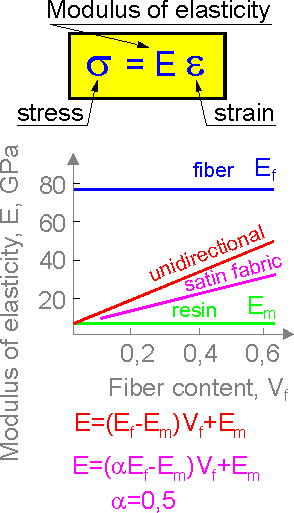 The
modulus of elasticity of a composite material depends on the
component's parameters, fiber content and structure of the
composite.
Boron, aramid, carbon fibers are more rigid
than an aluminum or epoxy matrix:
The
modulus of elasticity of a composite material depends on the
component's parameters, fiber content and structure of the
composite.
Boron, aramid, carbon fibers are more rigid
than an aluminum or epoxy matrix:
Ef >> Em
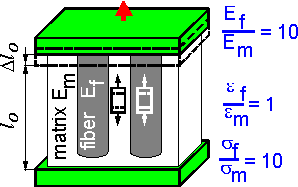 Both
the matrix and fibers have the same strain under tension.
Stress
is higher in the more rigid component.
Both
the matrix and fibers have the same strain under tension.
Stress
is higher in the more rigid component.
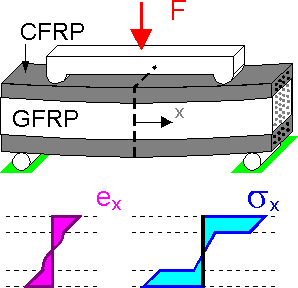 The
stress pattern in a composite beam demonstrates higher stress in
rigid components and in external layers. Local delaminations and
voids have a small effect on the flexural stiffness of the composite
beam.
The
stress pattern in a composite beam demonstrates higher stress in
rigid components and in external layers. Local delaminations and
voids have a small effect on the flexural stiffness of the composite
beam.
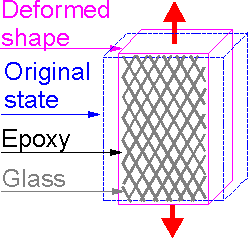 Poisson's
ratio is a measure of transverse deformation under tension
(compression).
An ordinary value of Poisson's ratio is 0.3 for
steels.
There is lay-up scheme for which transverse deformation
in a composite is higher in the longitudinal direction. Heres,
Poisson's ratio is higher than 1.
Poisson's
ratio is a measure of transverse deformation under tension
(compression).
An ordinary value of Poisson's ratio is 0.3 for
steels.
There is lay-up scheme for which transverse deformation
in a composite is higher in the longitudinal direction. Heres,
Poisson's ratio is higher than 1.
9.4 Strength
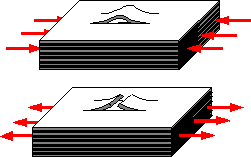 The
mechanisms of fracture of a laminate are different under tension and
compression. Surface layers can lose stability under compression.
The
mechanisms of fracture of a laminate are different under tension and
compression. Surface layers can lose stability under compression.
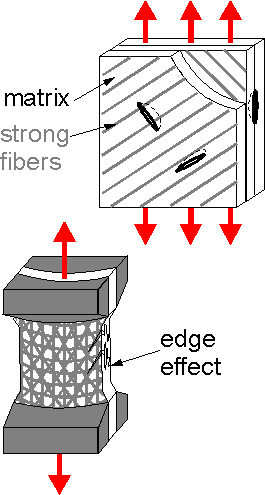 Inner
defects and edges are sources of fracture initiation. Transfibrous
defects are the most dangerous. Delamination has no great effect on
strength of the composite system.
Inner
defects and edges are sources of fracture initiation. Transfibrous
defects are the most dangerous. Delamination has no great effect on
strength of the composite system.
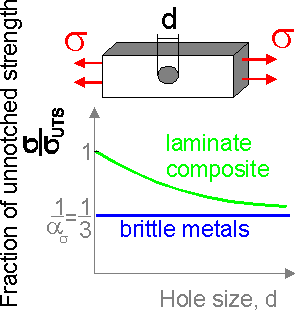 Holes
and cracks decrease the tensile strength of composites. Composite
materials are less В«sensitiveВ»
to small defects.
Holes
and cracks decrease the tensile strength of composites. Composite
materials are less В«sensitiveВ»
to small defects.
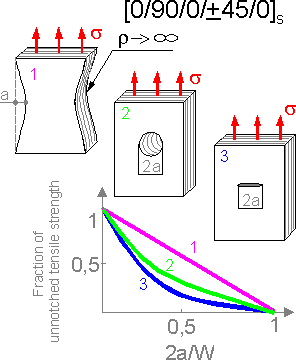 Cracks
perpendicular to the applied load are more dangerous than a hole with
the same maximum size.
Cracks
perpendicular to the applied load are more dangerous than a hole with
the same maximum size.
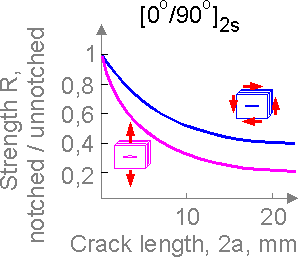 Tensile
strength reduces В«fasterВ»
than shear strength in presence of voids and cracks in multi-layer
composites.
Tensile
strength reduces В«fasterВ»
than shear strength in presence of voids and cracks in multi-layer
composites.
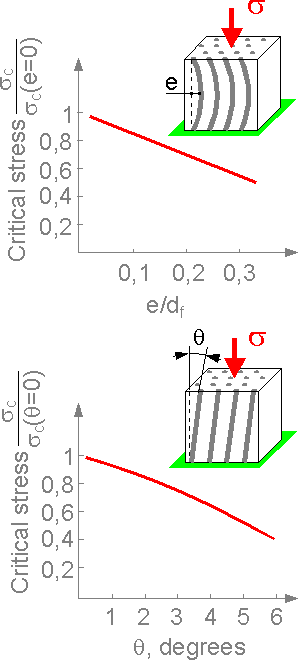 Curved
and inclined fibers decrease the compression strength of the
composite. The first factor is more critical in reducing the
strength.
Curved
and inclined fibers decrease the compression strength of the
composite. The first factor is more critical in reducing the
strength.
9.5 Crack resistance
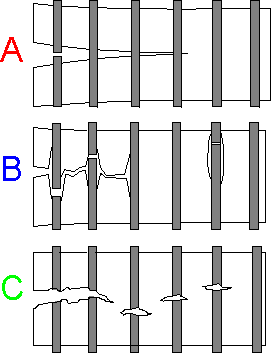 Multi-component
materials demonstrate high crack resistance. Mechanical properties of
the components and their bonds define the crack resistance of the
composite, such as tensile strength of matrix (A - the property is
low), bond strength (B), tensile strength of fibers (C). A matrix
with higher ductility and high-strength fibers is peculiar to high
crack resistance.
Multi-component
materials demonstrate high crack resistance. Mechanical properties of
the components and their bonds define the crack resistance of the
composite, such as tensile strength of matrix (A - the property is
low), bond strength (B), tensile strength of fibers (C). A matrix
with higher ductility and high-strength fibers is peculiar to high
crack resistance.
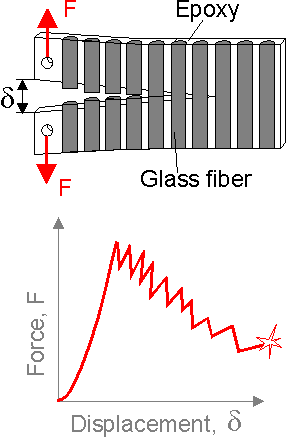 Each
fiber breakage is reflected in a peak in the В«force-displacementВ»
diagram. The critical force for the first fiber is larger than for
others.
Each
fiber breakage is reflected in a peak in the В«force-displacementВ»
diagram. The critical force for the first fiber is larger than for
others.
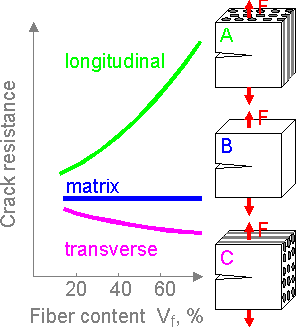 Unidirectional
composites have a high crack resistance if the maximum tensile stress
acts along the fibers. Tension in the transverse direction
demonstrates a crack resistance that is lower than the same parameter
for a ductile matrix.
Unidirectional
composites have a high crack resistance if the maximum tensile stress
acts along the fibers. Tension in the transverse direction
demonstrates a crack resistance that is lower than the same parameter
for a ductile matrix.
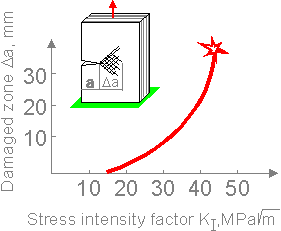 The
damaged zone in the crack tip in a multi-directional laminate depends
on the stress intensity factor (SIF). The SIF is the driving force in
fatigue crack growth equations.
The
damaged zone in the crack tip in a multi-directional laminate depends
on the stress intensity factor (SIF). The SIF is the driving force in
fatigue crack growth equations.
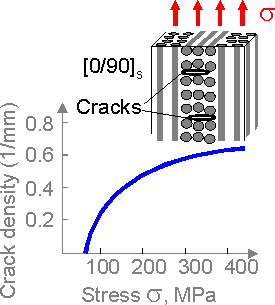 For
[0o/90o]s
lay-up, the transverse layer is the weakest. It starts to fracture by
small microcracking, final failure occurs when the microcracks
penetrate the longitudinal layer.
For
[0o/90o]s
lay-up, the transverse layer is the weakest. It starts to fracture by
small microcracking, final failure occurs when the microcracks
penetrate the longitudinal layer.
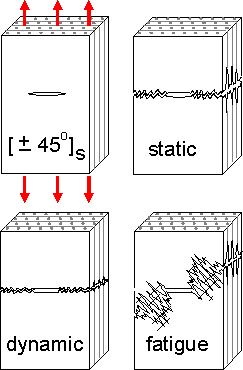 A
specimen fractured in a fatigue test has a great deal of debonding
and extracted fibers. Microdamage is less if a specimen was fractured
at high deformation rate.
A
specimen fractured in a fatigue test has a great deal of debonding
and extracted fibers. Microdamage is less if a specimen was fractured
at high deformation rate.
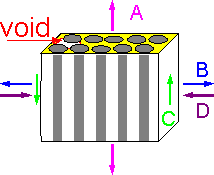 Voids
in matrix decrease the strength of unidirectional composites. The
effect of strength decrease is highest for transverse tension and
shear, lower for tension along the fibers.
Voids
in matrix decrease the strength of unidirectional composites. The
effect of strength decrease is highest for transverse tension and
shear, lower for tension along the fibers.
