7.2 Mechanical properties

The mechanical properties of materials are primarily determined subjecting a material sample to a tension test. During a tension test the sample is gradually loaded and the force and corresponding induced elongation are recorded. In order to compare the results obtained with samples of different dimensions the quanitities of stress and strain are utilized. Stress, s = P/A [N/m=Pa] where P - force applied to the sample; A - cross sectional area of the sample. Strain, e = Dl/l_o x 100% [%] where Dl = l - l_o; l - current length; l_o - initial length of the sample; The basic mechanical properties of a material can be acquired from the stress-strain diargam which results from a tensile test. To determine the yield stress from a stress-strain curve: 1. Find the point of 0.002 = 0.2% on the strain axis . 2. Draw a line parallel to the elastic region of the curve. 3. The intersection of the line and stress-strain curve corresponds to the yield stress of the material. The ultimate tensile strength is defined as the maximum value of stress reached in tensile test before fracture of the sample. Ductility can be determined in a material with the use of the following: Elongation = (l_f - l_o)/l_o x 100% Reduction in area = (A_f - A_o)/A_o x 100% where indexes o and f correspond to initial and final values at fracture respectivily. 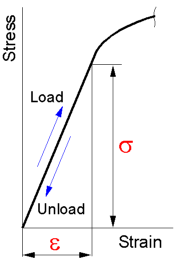The measure of material stiffness is defined as the elastic modulus. This quantity is determined from the initial range of the stress-strain diagram during which the material exhibits linear elastic behavior. In this region the sample will return to its original shape and dimensions upon unloading. Elastic modulus, E = s/e [Pa] The resistance to deformation in a material increases as the magnitude of the elastic modulus becomes greater. 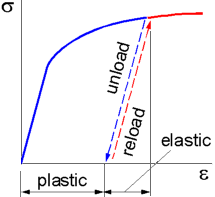Consider a test when a material is loaded beyond its yield stress. Upon unloading the stress follows a line parallel to the elastic range of the stress-strain curve. Futhermore, only the elastic deformation is recovered. The yield stress of a plastically deformed material is higher than its initial value. Upon reapplying the load the material deforms elastically until the new yield stress is reached. It should be noted that the elastic modulus of the material remains constant. 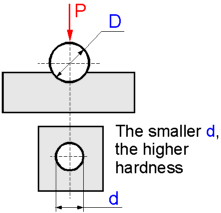Hardness is the ability of a material to resist the indentation of a harder solid. The most common hardness tests are accomplished by forcing a small indenter into the surface of the sample material. The picture shows the setup of the Brinell's hardness test. In general, hardness is proportional to the tensile strength of the material as both characteristics show a resistance of the material to plastic deformation.

7.3 Failure

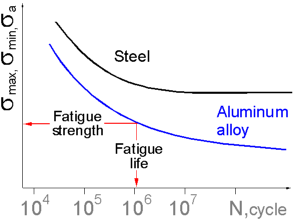The Fatigue curve or S-N curve is a plot of the number of cycles that a specimen will sustain at various levels of alternating stress or strain before failure. The maximum stress, minimum stress or stress amplitude can be utilized in the plot. A log scale is often used for the N axis. The S-N curves of materials such as high strength steels, aluminum alloys or materials in an aggressive environment do not have the horizontal segment. Fatigue Strength is the maximum stress that can be applied repeatedly for a specific number of cycles without leading to fracture. This quantity is usually determined directly from the S-N diagram. 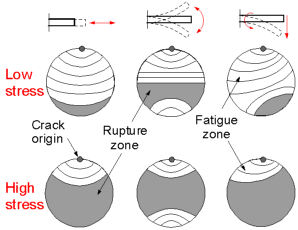Specimen loading (tension, bending or torsion) and a level of applied nominal stress can be indentified by examining the fracture surfaces. The fatique area has a fine structure outline and occupies nearly the whole section of a specimen if the applied stress is low. Similarly, a specimen which has endured a higher stress displays a smaller fatigue zone and a larger rupture zone. Площадь под кривая напряжение деформация представляет работу, необходимую для разрушения материала. Соответственно, чем больше площадь, тем больше работы необходимые для отказа фирмы. Пластичные материалы имеют обширные пластической деформации и высокое поглощение энергии до разрушения. Пластической деформации и поглощение энергии хрупких материалов являются относительно низкими. 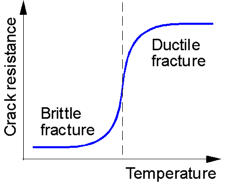Низкая температура уменьшается способность материала к пластической деформации. Материалы, которые пластичного при комнатной температуре показывают хрупкому разрушению при низких температурах. Исключение, такое поведение является большинство of materials with an FCC structure, which remain ductile at very low temperatures. At a narrow temperature range the crack resistance falls drastically. This is known as the ductile-to-brittle transition. 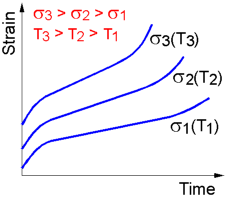Creep is the gradual increase of plastic deformation of a material under a constant stress, which is less than the yield stress. Creep is pronounced at temperatures above 0.4 of the melting point (taken in oK). The greater the service temperature or applied stress, the less time the material takes to fracture due to creep. 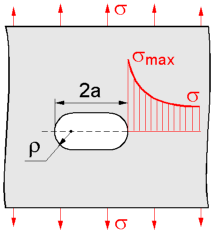The maximum stress, near the tip of an elliptical opening, perpendicular to the applied stress in a plane is determined from the following: smax = s x [1 + 2 x (a/r)^1/2] where s is the applied stress; r is the radius of curvature at the tip; a is the half length for an internal opening and the full length for a surface opening. 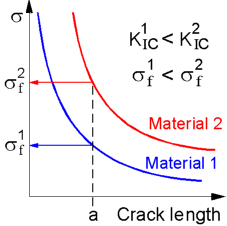Critical stress intensity factor K_IC or fracture toughness demonstrates the resistance of a material to the crack propagation. Damaged materials with higher fracture toughness can sustain a higher stress. The maximum nominal stress that a structural element with a crack can sustain, is determined as: s = K_IC / [Y (p x a)^1/2] where a is the half of the crack length; Y is a dimensionless factor depending on geometry. For a through internal crack that is much smaller than the dimensions of the element Y=1, for a surface crack Y=1.12.