
- •Главная
- •1.1 Напряжений и концентраторы
- •1.1.3 Концентраторы напряжения
- •1.3 Stress concentration factor
- •1.7 Elastic-plastic stress concentration
- •1.8 Joints: bolts and welds
- •3. Механические свойства конструкционных материалов
- •3.1 Напряженности испытания
- •3.2 Stress - strain diagram
- •3.3 Testing schemes
- •3.4 Strength
- •4 Прочность материалов
- •4.1 Tension and compression
- •4.2 Shear and torsion
- •4.3 Stress-strain state
- •4.4 Bending: force and moment diagrams
- •4.5 Geometrical characteristics of sections
- •4.6 Bending: stress and deformation
- •4.7 Mixed mode loading
- •4.8 Buckling
- •4.9 Statically indeterminate systems
- •4.10 Three-dimensional structures
- •References
- •5. Theory of elasticity
- •5.1 Deformation
- •5.2 Stress
- •5.3 Hooke's law
- •5.4 Plane problems
- •5.5 Torsion
- •5.6 Bending
- •5.7 Polar coordinates
- •5.8 Plates
- •5.9 Shells
- •5.10 Contact stresses
- •6.2 Distribution functions
- •6.3 Structural models of reliability
- •6.4 Limiting state
- •6.5 Dispersion
- •6.6 Durabilty
- •6.7 Design by reliability criterion
- •6.8 Risk
- •6.9 Safety classes
- •6.10 Risk : structural and social
- •References
- •7 Materials science
- •7.1 Crystalline solids
- •7.2 Mechanical properties
- •7.3 Failure
- •7.4 Phase diagrams
- •7.5 Heat treatment of metals and alloys
- •7.6 Corrosion of metals and alloys
- •7.7 Casting
- •7.8 Polymers
- •7.9 Composites
- •7.10 Forming of metals
- •8.2 Mechanical properties
- •8.3 Stress concentration
- •8.4 Defects
- •8.5 Residual Stress
- •8.6 Strength
- •8.7 Fatigue strength
- •8.8 Fracture
- •8.9 Weldability
- •References
- •9 Composites
- •9.1 Structure of composites
- •9.2 Fibers
- •9.3 Rigidity
- •9.4 Strength
- •9.5 Crack resistance
- •9.6 Optimization
- •9.7 Fatigue and temperature effect
- •9.8 Reliability
- •9.9 Joints
- •9.10 Material selection
- •References
- •10 Finite element analysis
- •10.1 Finite element method
- •10.2 Finite elements
- •10.3 Meshing
- •10.4 Boundary conditions
- •10.5 Deformation
- •10.6 Accuracy
- •10.7 Heat transfer analysis
- •10.8 Dynamics
- •10.9 Computational fluid dynamics
- •10.10 Design analysis
- •References
6.10 Risk : structural and social
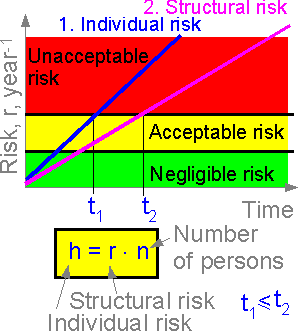 Structural
risk is connected with individual and social risks. Individual risk
is equal to structural risk times the number of structural elements
and number of people at risk.
The figure shows the
structural and individual risks for a space shuttle. The individual
risk of the crew member is the most important consideration, service
with unacceptable individual risk (t > t1)
cannot be recommended. The more crew members, the higher the
individual risk.
Structural
risk is connected with individual and social risks. Individual risk
is equal to structural risk times the number of structural elements
and number of people at risk.
The figure shows the
structural and individual risks for a space shuttle. The individual
risk of the crew member is the most important consideration, service
with unacceptable individual risk (t > t1)
cannot be recommended. The more crew members, the higher the
individual risk.
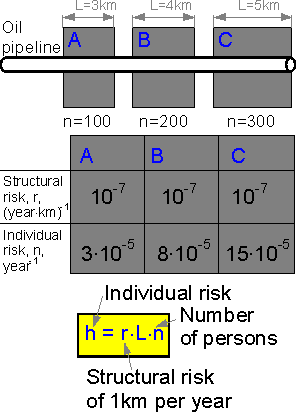 If
an oil pipeline passes near a settlement the structural risk for L
kilometers of the pipeline is equal to L times the structural risk of
one kilometer. The more people in the settlement, the bigger the
individual risk.
If
an oil pipeline passes near a settlement the structural risk for L
kilometers of the pipeline is equal to L times the structural risk of
one kilometer. The more people in the settlement, the bigger the
individual risk.
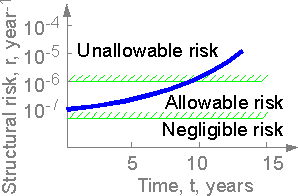 The
structural risk of a severe accident of a structure can increase with
time. If the risk exceeds the allowable value from corresponding
industry standards the management of long-time service should be
considered.
The
structural risk of a severe accident of a structure can increase with
time. If the risk exceeds the allowable value from corresponding
industry standards the management of long-time service should be
considered.
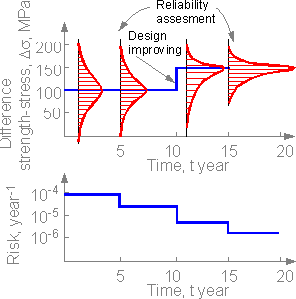 Another
situation where a unique engineering structure is assessed for safety
and improvements were made in the structural elements. There are no
severe accidents. Safety assessments, knowledge of the likelihood of
failure scenarios, and the design improvement can decrease risk. The
more knowledge the smaller the risk.
Another
situation where a unique engineering structure is assessed for safety
and improvements were made in the structural elements. There are no
severe accidents. Safety assessments, knowledge of the likelihood of
failure scenarios, and the design improvement can decrease risk. The
more knowledge the smaller the risk.
 The
human factor plays a significant role. Nuclear power stations have
backup systems and special nondestructive testing and inspections
that decrease the risk.
The
human factor plays a significant role. Nuclear power stations have
backup systems and special nondestructive testing and inspections
that decrease the risk.
 Statistics
can help choose a profession with lowest risk. Fortunately, other
factors such as salary and interest also affect the decision.
Statistics
can help choose a profession with lowest risk. Fortunately, other
factors such as salary and interest also affect the decision.
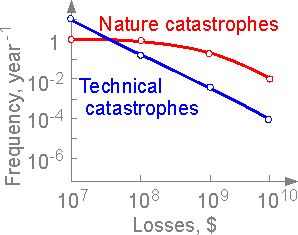 Losses
due to natural catastrophes such as tornadoes, earthquakes, forest
fire, etc. at level 1010
are more valuable. More losses are connected with natural
catastrophes than technical disasters.
Losses
due to natural catastrophes such as tornadoes, earthquakes, forest
fire, etc. at level 1010
are more valuable. More losses are connected with natural
catastrophes than technical disasters.
References
Hahn G.J.,Shapiro S.S. Statistical Models in Engineering , John Wiley & Sons, 1994.
Kapur K.C. , Lamberson L. R. Reliability in Engineering Design , John Wiley & Sons, 1977.
Kumamoto H., Henley E.J. Probabilistic Risk Assessment and Management for Engineers , Inst of Electrical Engineers, 1996.
Madsen H.O., Krenk S., Lind N.C.Methods of Structural Safety, Prentice-Hall Inc., 1986.
Olkin I., Gleser L.J., Derman C.Probability Models and Aplications, Macmillan Publishing Co., Inc., 1980.
Tichy M. Applied Methods of Structural Reliability , Kluwer Academic Pub., 1993.
THEMES
Theme 1. Stress Concentration Theme 2. Fracure Mechanics Theme 3. Mechanical Properties Theme 4. Strength of Materials Theme 5. Theory of Elasticity Theme 6. Structural Safety Theme 7. Material Science Theme 8. Welds Theme 9.Composite Materials Theme 10. Finite Element Analysis
7 Materials science
Andrei Burov
7.1 Crystalline solids
 The
smallest repeating unit in a crystal is called the unit cell. The
geometry and the position of the particles within the unit cell
determine the structure of crystalline materials. Three edge lengths
(a, b, c) and internal angles (a, b, g) will be used to describe the
geometry of a unit cell. There are seven crystal systems and fourteen
possible unit cells (Bravais unit cells) depending on the values of
a, b, c and a, b, g.
The
smallest repeating unit in a crystal is called the unit cell. The
geometry and the position of the particles within the unit cell
determine the structure of crystalline materials. Three edge lengths
(a, b, c) and internal angles (a, b, g) will be used to describe the
geometry of a unit cell. There are seven crystal systems and fourteen
possible unit cells (Bravais unit cells) depending on the values of
a, b, c and a, b, g.
 Some
of the particles within a unit cell may be shared and therefore do
not belong completely to an individual cell. Therefore, in order to
calculate number of particles per unit cell we have to consider the
following contributions for each particle according to its
position:
- atoms centered on the face count 1/2;
- atoms
centered on the edge count 1/4;
- atoms centered on the vertex
count 1/8
In a simple cubic number of atoms per unit cell = 1;
in a body centered cubic - 2; in a face centered cubic - 4.
Atomic
packing factor = (Volume of atoms)/(Volume of unit cell). For a
simple cubic - atomic packing factor = 0.52; a body centered cubic -
0.68; a face centered cubic - 0.74
Some
of the particles within a unit cell may be shared and therefore do
not belong completely to an individual cell. Therefore, in order to
calculate number of particles per unit cell we have to consider the
following contributions for each particle according to its
position:
- atoms centered on the face count 1/2;
- atoms
centered on the edge count 1/4;
- atoms centered on the vertex
count 1/8
In a simple cubic number of atoms per unit cell = 1;
in a body centered cubic - 2; in a face centered cubic - 4.
Atomic
packing factor = (Volume of atoms)/(Volume of unit cell). For a
simple cubic - atomic packing factor = 0.52; a body centered cubic -
0.68; a face centered cubic - 0.74
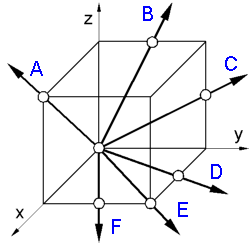 To
determine a crystallographic direction [uvw] in a unit cell:
1.
Find the vector projections on the three axes.
A - 1,0,1; B -
0,1/2,1; C - 0,1,1/2;
D - 1/2,1,0; E - 1,1,0; F - 1,1/2,0.
2.
Reduce these coordinates to the 3 smallest integers having the same
ratio.
A - [101]; B - [012]; C - [021];
D - [120]; E -
[110]; F - [210].
To
determine a crystallographic direction [uvw] in a unit cell:
1.
Find the vector projections on the three axes.
A - 1,0,1; B -
0,1/2,1; C - 0,1,1/2;
D - 1/2,1,0; E - 1,1,0; F - 1,1/2,0.
2.
Reduce these coordinates to the 3 smallest integers having the same
ratio.
A - [101]; B - [012]; C - [021];
D - [120]; E -
[110]; F - [210].
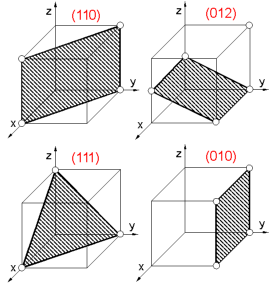 A
plane within a crystal is defined by the Miller indices. To determine
crystallographic (Miller) indices (hkl) of the plane:
1. Find
intercepts of a plane on the three axes in terms of the unit cell
dimensions.
2. Determine the reciprocals of these numbers.
3.
Reduce the reciprocals to the three smallest integers.
A
plane within a crystal is defined by the Miller indices. To determine
crystallographic (Miller) indices (hkl) of the plane:
1. Find
intercepts of a plane on the three axes in terms of the unit cell
dimensions.
2. Determine the reciprocals of these numbers.
3.
Reduce the reciprocals to the three smallest integers.
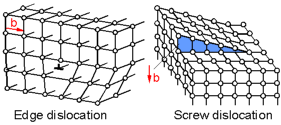 There
are two main types of planar defects called dislocations - edge
dislocation and screw dislocation. A dislocation is a sharp change in
the order of atoms along a line. Dislocations move on the slip plane.
The magnitude and direction of the slip is defined by the Burger's
vector, b. For an edge dislocation the direction of slip is
perpendicular to the direction of the dislocation. For a screw
dislocation the direction of slip is parallel to the direction of the
dislocation.
There
are two main types of planar defects called dislocations - edge
dislocation and screw dislocation. A dislocation is a sharp change in
the order of atoms along a line. Dislocations move on the slip plane.
The magnitude and direction of the slip is defined by the Burger's
vector, b. For an edge dislocation the direction of slip is
perpendicular to the direction of the dislocation. For a screw
dislocation the direction of slip is parallel to the direction of the
dislocation.
 Slip
is known to occur on planes (shown on the picture) in the direction
of the maximum density of atoms. This is called a slip system. If
there are many slip systems then deformation can occur relatively
easily and the metal is considered ductile. BCC crystal structure has
up to 48 slip systems. FCC crystal structure has 12 slip systems. HCP
crystal structures have only 3 slip systems. Accordingly, most metals
with a HCP crystal structure (Mg, Zn, Be) are less ductile than
metals with a BCC (W, Fe, K) or FCC (Cu, Al, Ni) structure.
The
distance between atoms varies depending on the crystallographic
directions. This is the cause of the anisotropy of mechanical and
physical properties of a crystal. Therefore, samples cut from a
monocrystal in different directions will exhibit a difference in the
stiffness. In the FCC and BCC crystals of metals the highest elastic
modulus is found in [111] direction, while the lowest is found in the
direction of [100]. Real materials consist of many chaotically
oriented monocrystals, which results in the isotropy of their
properties.
Slip
is known to occur on planes (shown on the picture) in the direction
of the maximum density of atoms. This is called a slip system. If
there are many slip systems then deformation can occur relatively
easily and the metal is considered ductile. BCC crystal structure has
up to 48 slip systems. FCC crystal structure has 12 slip systems. HCP
crystal structures have only 3 slip systems. Accordingly, most metals
with a HCP crystal structure (Mg, Zn, Be) are less ductile than
metals with a BCC (W, Fe, K) or FCC (Cu, Al, Ni) structure.
The
distance between atoms varies depending on the crystallographic
directions. This is the cause of the anisotropy of mechanical and
physical properties of a crystal. Therefore, samples cut from a
monocrystal in different directions will exhibit a difference in the
stiffness. In the FCC and BCC crystals of metals the highest elastic
modulus is found in [111] direction, while the lowest is found in the
direction of [100]. Real materials consist of many chaotically
oriented monocrystals, which results in the isotropy of their
properties.
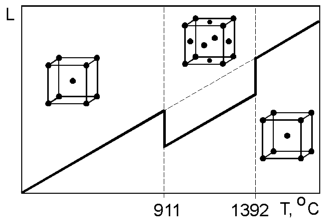 Some
materials can exist with different crystal structures. This can be
demonstrated by pure iron which has a body centered cubic (BCC)
structure at room temperature and a face centered cubic (FCC)
structure at 911 oC.
This change is accompanied by shrinkage in volume due to the FCC
structure being more closely packed than the BCC structure. The
second transformation of crystal structure from FCC to BCC occurs at
1392 oC.
Some
materials can exist with different crystal structures. This can be
demonstrated by pure iron which has a body centered cubic (BCC)
structure at room temperature and a face centered cubic (FCC)
structure at 911 oC.
This change is accompanied by shrinkage in volume due to the FCC
structure being more closely packed than the BCC structure. The
second transformation of crystal structure from FCC to BCC occurs at
1392 oC.
