5.9 Shells

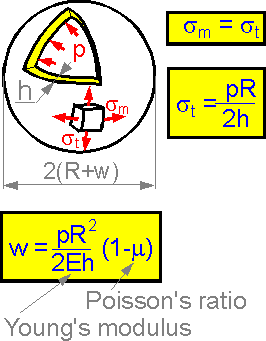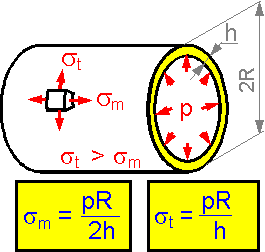The tangential stress is equal to meridian stress for spherical shells. Radial displacement (radius increase) is directly proportional to the inner pressure and R². The bigger the Young's modulus of the material, the smaller the displacement. The tangential stress for a cylindrical pressure vessel is twice as large as the meridian stress. 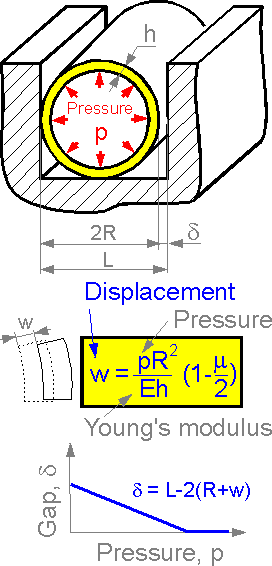The radial displacement is proportional to pressure. The bigger the displacement, the smaller the gap between the cylindrical vessel and the wall. There is a pressure when the gap is zero. 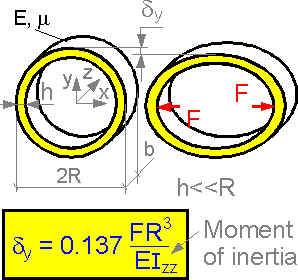Tension in the X-direction results in deformation in the vertical direction. This theory gives the formula for calculation of the displacement d_y. 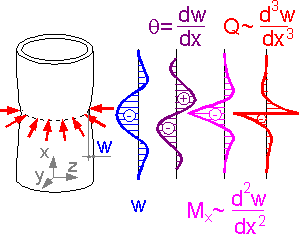A cylindrical shell is compressed. The figure shows patterns of deflection w, angle of rotation q, bending moment M and transverse force Q. 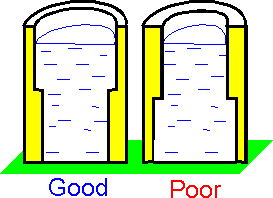The bending moment and bending stress are at a maximum at the bottom of the tank. The most effective use of material utilizes thicker parts at the bottom. 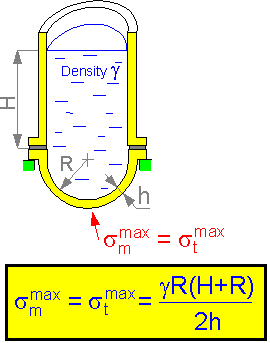The tangential and radial stresses are at a maximum in the bottom of the water tank. There is a quadratic dependence of the stress on the radius of the half-sphere R. 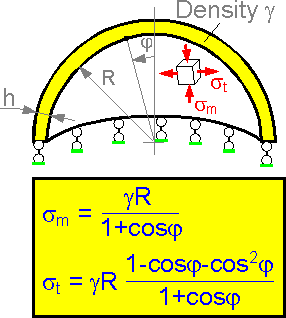If a spherical dome accepts its own weight, the increase in thickness h results in an increase of the shell weight and its bending rigidity. The two factors compensate for each other. Therefore, maximum stress does not depend on thickness of the shell. 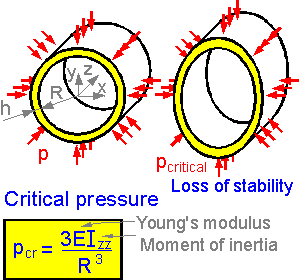A thin-walled cylindrical ring can lose its shape due to a pressure increase. The more rigid the material, the bigger the critical stress. Critical pressure is proportional to Young's modulus E. 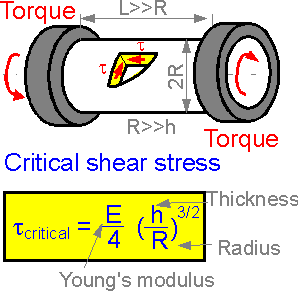A thin wall cylindrical shell can lose stability at shear stress t_critical. Geometrical parameters have different effects on the critical stress. Length L has no effect on the critical stress t_critical. The bigger the radius R, the smaller the stress. The bigger the thickness h, the bigger the critical stress t_critical.

5.10 Contact stresses

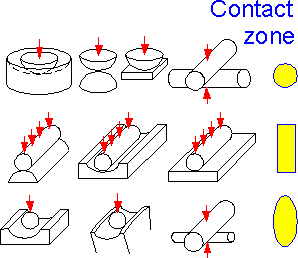The shape of the contact area between two elastic bodies is usually circular, elliptical or rectangular. This is valid for ideal elastic bodies. 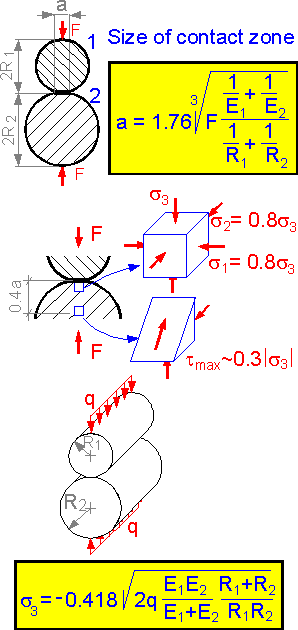The size of the contact area depends on the modulus of elasticity of the balls, their radii and the compressive force F. It is proportional to F^1/3. Absolute value of the contact normal stress s₃ is at a maximum at the contact surface. The two other components are 80% of s₃. Maximum shear stress acts inside the ball at 0.4a from the surface. 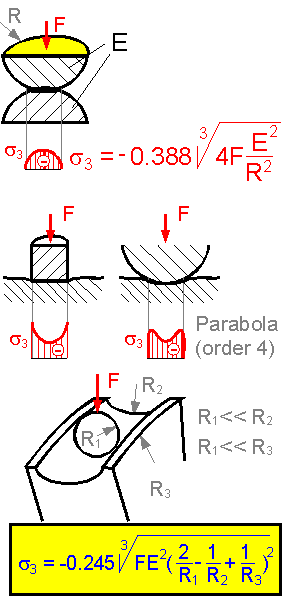For compression of two balls the contact stress is at a maximum in the center of the contact spot. The stress decreases to zero at the edges of the contact region. For the two other loading situations, the stress is not the highest in the center. The theory of elasticity predicts the maximum contact stress for ball bearings. The smaller contact stress, the better. The smaller the modulus of elasticity E, the smaller the contact stress. The hardness, not the contact stress, is more important in choosing the material for ball bearings. 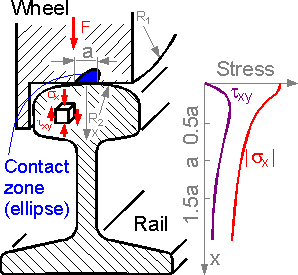Shear stress in a rail is approximately equal to zero at the surface (z=0) and is at a maximum at a distance 0.45a from the contact zone, where a is size of contact region. 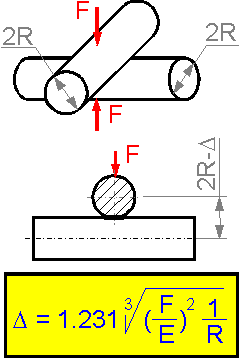The distance between the centers of the cylinders decreases with an increase in force. There is no linear dependence for the elastic displacement D. 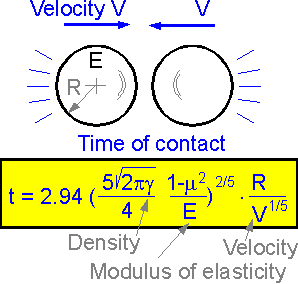Time of contact for impact between two steel balls in a ball mill is proportional to the radius of the balls R. Increase in the modulus of elasticity or in velocity decreases the time of contact. The bigger the size of the balls the longer the time of contact.

REFERENCES

S.P. Timoshenko, J.N. Goodier Theory of Elasticity, McGraw-Hill, N. Y., 1970.

S.P. Timoshenko, S. Woinowsky-Krieger Theory of Plates and Shells, McGraw-Hill, N. Y., 1959.

THEMES

Theme 1. Stress Concentration Theme 2. Fracure Mechanics Theme 3. Mechanical Properties Theme 4. Strength of Materials Theme 5. Theory of Elasticity Theme 6. Structural Safety Theme 7. Material Science Theme 8. Welds Theme 9.Composite Materials Theme 10. Finite Element Analysis

6. STRUCTURAL SAFETY

Igor Kokcharov and Anatolii Lepikhin

6.1 RELIABILITY

Dependability is the ability of a structure to maintain its working parameters in given ranges for a stated period of time. Dependability is a collective term used to describe the availability performance and its influencing factors: reliability performance, maintainability performance and maintenance-support performance. Dependability is used only for general descriptions in non-quantitative terms. Maintainability is a measure of the ease and rapidity with which a system can be restored to operational status following a failure. 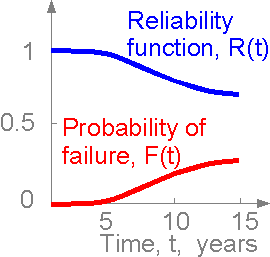Reliability is the probability of component or system success under stated conditions for a stated period of time. Time to the moment when the structure fails is not exactly known. The time is a random variable. Reliability is characterized by the reliability function R(t):

R(t) = P{t > t}

where P is the probability that the operating time to failure t exceeds the stated period of time t. Probabilities are numbers between 0 and 1. The reliability function is related to the probability of failure function F(t) and its density function f(t):

F(t) = 1 - R(t) ; f(t) = d F(t) / dt = - d R(t) / dt;

The domain of the cumulative distribution function F(t) is from zero to infinity, while its range is the interval [0 ... 1]. 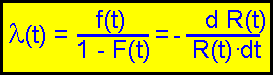Failure rate l(t) is an important parameter of reliability. Every random variable has its associated cumulative distribution function. The cumulative distribution function F(t) is increasing (accumulating probability) as t increases. If the failure rate is constant (exponential law of reliability) the dependence between failure rate and reliability function can be simplified. 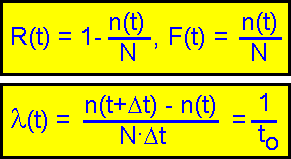Statistical estimators of the function can be obtained by the following expressions. Here: n(t) - number of failed elements to time t. N - total number of elements. to - mean time to failure. There is some standard behavior of the dependence curve of failure rate l versus time t: 1. failures due to manufacturing defects (cracks, inappropriate materials, poor design) 2. failures due to conditions of service (exploitation errors) 3. 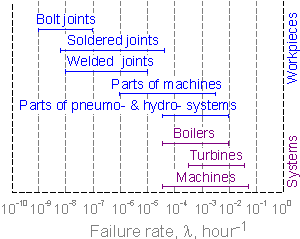failures due to accumulated damage (wear and fatigue) The figure shows typical ranges of failure rate for different engineering systems. The parameter changes over a wide range.