Пабочны эфект

Калі пры выкліку падпраграмы акрамя змянення параметраў-пера­мен­ных адбываюцца змяненні нейкіх глабальных аб’ектаў, то гэта на­зы­ва­ецца пабочным эфектам.

Пабочны эфект лічыцца непажаданай з’явай, бо ён можа прывесці да не­кантралюемасці сітуацыі. Асабліва шкодны пабочны эфект для функ­цыі.

Асноўнае прызначэнне функцыі – па яе параметрах атрымаць вынік. Калі пры гэтым змяняюцца глабальныя пераменныя ці параметры-пе­ра­мен­ныя, тады змест функцыі становіцца няясным.

Прыклад 1.

PROGRAM SideEffect;

VAR k : Integer;

FUNCTION Fact (VAR n : Integer) : Longint;

VAR f : Longint;

BEGIN

f:=1;

REPEAT

f := f * n;

n := n - 1;

UNTIL n = 1;

Fact := f

END;

FUNCTION Fk(k : Integer) : Integer;

BEGIN

Fk := k;

END;

BEGIN

k := 3; Writeln (k, ' ', Fk(k) + Fact(k));

k := 3; Writeln (k, ' ', Fact(k) + Fk(k));

END;

Наша падпраграма Fact змяняе параметр-пераменную. Па прычыне гэтага пабочнага эфекту ад перамены месц складаемых змяніўся вынік. Тут трэба замест параметра-пераменнай (VAR) паставіць параметр-зна­чэн­не.

Многія сучасныя мовы праграміравання змяшчаюць прамыя забароны на падобныя дзеянні.

Прыклад 2.

PROGRAM SideEffect_2;

VAR a, d, z : Integer;

FUNCTION Change(x : Integer) : Integer;

BEGIN

z := z - x; {змяненне глабальнай пераменнай}

Change := Sqr(x); {аргумент у квадрат}

END;

BEGIN

z := 10; a := Change(z); Writeln(a, z); {100, 0}

z := 10; d := 10; a := Change(d) * Change(z);

Writeln(a, z);

z := 10; d := 10; a := Change(z) * Change(d);

Writeln(a, z);

END;

Выканаем праграму на камп’ютары і параўнаем адказы. Відаць, што яны розныя.

Заўвага 1. Трэба пазбягаць залежнасці падпраграм ад глабальных у ад­но­сі­нах да яе пераменных.

Заўвага 2. Параметр-масіў лепш апісваць як параметр-пераменную (VAR) ці як параметр-канстанту (CONST), каб кампілятар не будаваў ко­пію ма­сі­ву як лакальную пераменную і не перасылаў туды значэнні. Такім чынам мы эканомім і памяць, і час выканання праграмы. Гэта адносіцца і да іншых скла­да­ных тыпаў даных.

Але для параметраў тыпу FILE ёсць наступнае абмежаванне: такія па­ра­мет­ры заўсёды павінны быць параметрамі-пераменнымі (з VAR).

Рэкурсія і ітэрацыі

Для большасці вылічальных задач ітэрацыя – паслядоўнае вы­лі­чэн­не – аказваецца эфектыўней, чым рэкурсія, але для многіх задач, якія пра­цу­юць з данымі складанай структуры, выкарыстанне рэкурсіі з’яўля­ец­ца пе­раважным.

У целе падпраграмы вядомы (даступны) усе аб’екты, якія апісаны ў ахоп­лі­ва­ю­чым блоку, у тым ліку і імя самой падпраграмы. Такім чынам, унут­ры цела падпраграмы магчымы выклік самой падпраграмы.

Працэдуры і функцыі, якія выкарыстоўваюць выклікі «саміх сябе», на­зы­ва­юц­ца рэкурсіўнымі.

Дапушчальна таксама ўскосная рэкурсія, пры якой, напрыклад, пад­праг­ра­ма A выклікае падпраграму B, якая ў сваю чаргу выклікае пад­п­ра­гра­му C, а апошняя – першапачатковую падпраграму A.

Добра вядома, што існуе шмат рэкурсіўных матэматычных ал­га­рыт­маў, напрыклад вылічэнне n!:

n! = (n – 1)! * n, 0! = 1, 1! = 1.

FUNCTION Fact(N : Byte): Longint;

BEGIN

IF N = 0 THEN Fact := 1 ELSE Fact := N * Fact(N - 1);

END;

Выкананне рэкурсіўнай праграмы адбываецца ў два этапы.

 На першым этапе здзяйсняецца пабудова рэкурсіўных суадносін і час­т­ко­вае вылічэнне з затрымкай выканання дзеянняў, якія не могуць быць выкананы на дадзеным этапе.

Затрымка вылічэнняў абумоўлена тым, што ў апісанні рэкурсіўнай пад­п­раг­ра­мы заўсёды прысутнічае зварот да той самай падпраграмы.

Першы этап завяршаецца пасля выканання так званай умовы за­вяр­шэн­ня рэкурсіі. (Гэта дно рэкурсіі.)

 На другім этапе здзяйсняюцца вылічэнні дзеянняў на аснове рэ­кур­сіў­ных суадносін.

У мове Pascal няма ніякіх абмежаванняў на рэкурсіўныя выклікі пад­праг­рам, неабходна толькі добра разумець, што кожны чарговы рэ­кур­сіў­ны вык­лік прыводзіць да ўтварэння новай копіі лакальных аб’ектаў пад­пра­гра­мы, і ўсе гэтыя копіі, якія адпавядаюць ланцужку актывізаваных і не­за­вер­ша­ных рэкурсіўных выклікаў, існуюць незалежна адна ад адной.

Рэкурсіўныя падпраграмы – сродак, зручны для чалавека, але даволі нак­лад­ны для ЭВМ. Звычайна рэкурсіўныя падпраграмы прымяняюць пры не­вя­лі­кай глыбіні рэкурсіі, калі час ліку і затраты памяці не вельмі вя­лікія.

Праграміруючы рэкурсію, заўсёды трэба памятаць аб умове яе за­кан­чэн­ня, бо ў адваротным выпадку падпраграма будзе бясконца звяр­тац­ца сама да сябе і тэарэтычна ніколі не спыніцца, але хутчэй за ўсё пра­грама вы­чар­пае рэсурсы ПК, паколькі кожны зварот да падпраграмы па­трабуе чарговай пор­цыі аператыўнай памяці.

Трэба ўмець адрозніваць, дзе рэкурсія, а дзе ітэрацыя.

Наступныя алгарытмы прыстасуем да рэкурсіўных.

Задача 1. Падлічыць N-ы лік Фібаначы: f₀  = 1,  f₁  = 1,  f_n  = f_n–1 + f_n–2, n  2.

FUNCTION ChFR(n : Integer) : Integer;

BEGIN

IF (n = 0) OR (n = 1) THEN ChFR := 1

ELSE ChFR := ChFR(n - 2) + ChFR(n - 1)

END;

Задача 2. Знайсці НАД(a, b) (НАД – найбольшы агульны дзельнік).

FUNCTION HAD(a,b : Integer) : Integer;

BEGIN

IF b = 0 THEN HAD := a ELSE HAD := HAD(b, a MOD b)

END;

Задача 3. Падлічыць значэнне сумы элементаў

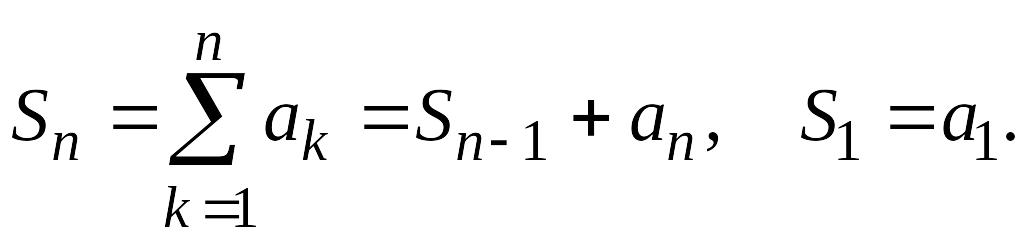
CONST k=50;

TYPE AR = ARRAY[1..k] OF Real;

VAR a : AR;

s : Real;

n, і : Integer;

FUNCTION Sum(VAR a : AR; n : Integer) : Real;

BEGIN

IF n = 1 THEN Sum := a[1]

ELSE Sum := Sum(a, n - 1) + a[n]

END;

BEGIN

n := 10;

FOR і := 1 TO n DO a[і] := Random * 100 - 50;

S := Sum(a, n);

Write('сума=', S);

END.

Задача 4. Знайсці найбольшае значэнне сярод лікаў .

Алгарытм. Зводзім пошук да Max{a, b}. Маем:

Max{a₁, …, a_n}=Max{Max{a₁, …, a_n-1}, a_n}, Max{a₁}=a₁

CONST n=15;

TYPE

Vect=ARRAY[1..n] OF Real;

VAR

i : Integer;

a : Vect;

FUNCTION Maximum(VAR a : Vect; n : Integer) : Real;

VAR M : Real;

BEGIN

IF n=1 THEN Maximum:=a[1]

ELSE

BEGIN

M:=Maximum(a, n-1);

IF M<=a[n] THEN Maximum:=a[n]

ELSE Maximum:=M

END;

END;

BEGIN

FOR i := 1 TO n DO Read(a[i]);

Writeln;

Writeln(Maximum(a, n):9);

Readln

END.