Оптимальное исследование рынка

Группе, исследующий рынок, требуется получить данные из n различных мест. В ее распоряжении имеется n дней, и она предполагает провести по одному дню в каждом месте, проведя по а_j опросов, j = 1, …, n. Вероятность успешного опроса в каждом месте задается матрицей Р. Элемент матрицы р_ij характеризует вероятность успешного опроса в течении i-го дня в j-м месте, i = 1, …, n.

Определить время проведения опросов, при котором общее число опросов максимально.

Сведем данную задачу к задаче о назначениях.

Введем величину r_ij = p_ija_j, показывающую число успешных опросов в в j-м месте в течение i-го дня.

1, если в i-й день опрос проводится в j-м месте;

x_ij =

0, в противном случае.

Математическая модель задачи имеет следующий вид:

;

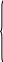
x_ij Î {0;1}, i = 1,…,n; j = 1,…,n.

Функция F характеризует суммарное число успешных опросов. Ее нужно максимизировать. Первое и второе ограничения соответствуют тому, что в течение одного дня можно находиться только в одном месте. Для расчета модели венгерским методом надо перейти к противоположной функции:

и в соответствующей таблице записывать значения r_ij с противоположным знаком.

Оптимальное использование торговых агентов

Торговая фирма продает товары в n различных городах, покупательная способность жителей которых оценивается b_j усл. ед., j = 1,…, n. Для реализации товаров фирма располагает n торговыми агентами, каждого из которых она направляет в один из городов. Профессиональный уровень агентов различен; доля реализуемых i-м торговым агентом покупательных способностей составляет а_i, i = 1,…,n. Как следует распределить торговых агентов по городам, чтобы фирма получила максимальную выручку от продажи товаров?

Решение этой проблемы может быть найдено с помощью задачи о назначениях. В качестве кандидатов выступают торговые агенты, в качестве работ – города.

Введем параметр с_ij = a_i b_j, характеризующий величину покупательных способностей, реализуемых i-м торговым агентом в j-м городе.

Управляющие переменные x_ij, i = 1,…, n; j = 1,…, n определяются по формуле

1 , если i-й агент направлен в j-й город;

x_ij =

0, в противном случае.

Математическая модель запишется в следующей форме:

;

x_ij Î {0;1}, i = 1,…,n; j = 1,…,n.

Первое и второе ограничения формализуют соответственно условию о том, что в каждый город направляется один торговый агент, и один торговый агент не может работать в двух городах. Целевая функция F – это сумма реализованных покупательных способностей всеми торговыми агентами во всех городах. Она должна подлежать максимизации. Для решения задачи венгерским методом надо, как и в предыдущем примере, перейти к противоположной функции.

Пример 3.2.

Компания разрабатывает план распределения торговых агентов по населенным пунктам. Предположим, что в качестве городов-претендентов рассматриваются Нальчик, Саратов, Казань, Ростов и Москва и в распоряжении менеджера на данный момент имеется 4 сотрудника. Покупательная способность жителей городов 1400, 5000, 3600, 4800 и 3000 шт. соответственно. Также известен процент успешно реализуемых покупательных способностей по продукции проекта для каждого сотрудника: 80, 60, 75 и 65%. Цена продажи рассматриваемой продукции составляет 3000 руб./шт. Ниже указаны издержки связанные с транспортировкой и проживанием агента в течение рассматриваемого проекта.

1. Транспортные издержки (тыс. руб.) в зависимости от исходного места дислокации сотрудника:

Вид продукции	Предприятие
	1	2	3	4	5
1	20	23	38	15	5
2	8	29	6	35	5
3	5	8	3	4	7

2. Бытовые издержки (тыс. руб.) сотрудника за весь период реализации проекта:

Вид продукции	Предприятие
	1	2	3	4	5
1	20	50	20	10	13
2	7	90	8	35	60
3	5	5	4	15	6

Необходимо разработать план распределения торговых агентов, чтобы прибыль при реализации проекта была максимальной.

Рекомендации. По имеющимся данным необходимо сформировать матрицу ожидаемой прибыли (доходы за вычетом издержек). Учтите, что задача состоит в поиске максимального значения целевой функции. Решите задачу венгерским методом.