
- •1. Типы структурных экономических моделей.Проблемы идентификации и оценивания параметров.
- •6.Статистические оценки и их характеристика.
- •11. Нуль-гипотеза и принцип ее проверки.
- •12.Модель экономического роста Солоу.
- •13. Задача нелинейного программирования и методы их решения. Теорема Куна-Таккера.
- •14. Классификация методов прогнозирования.
- •25. Относительные величины и их значение в статистике. Виды относительных величин и формы их выражения.
- •15. Кибернетический подход в логистике.
- •16. Игры двух лиц с нулевой суммой. Смешанные стратегии. Теорема Неймана. Аналитическое решение игры (2х2).
- •27. Таблица межотраслевого баланса. Основные балансовые соотношения.
- •17. Неоклассическая задача потребления.
- •18. Временные ряды. Их основные характеристики и процедуры сглаживания.
- •23. Производственная функция. Свойства производственных функций. Основные типы производственных функций.
- •28. Тест Дарбина-Уотсона на автокорреляцию по времени.
- •32.Показатели качества регрессии. Коэффициенты корреляции, детерминации, дисперсионное отношение Фишера, стандартные ошибки.
- •35. Задачи линейного программирования. Различные формы записи. Способ решения. Примеры задач.
- •33. Динамический межотраслевой баланс
- •34. Линейная регрессия в условиях мультиколлинеарности. Ридж-оценивание.
- •43. Модель сетевого планирования. Методы срн и pert.
- •47. Основные макроэкономические показатели.
- •49. Предмет и функции «Экономической теории»
- •80. Цель и роль информационных потоков в логистических системах. Структура инф-ной логистич системы как совокупности подсистем для функциональных областей логистики.
- •51. Рынок труда и безработица.
- •52. Совокупный спрос и совокупное предложение
- •55. Предпринимательский доход и экономическая прибыль. Источники экономической прибыли. Функции прибыли.
- •56. Заработная плата: сущность и факторы, ее определяющие. Зарплата в условиях конкурентного рынка.
- •57. Классификация рыночных структур: признаки совершенной конкуренции, монополистической конкуренции и чистой монополии.
- •58. Определение цены и объема производства в условиях чистой монополии (в двух временных периодах).
- •39.Модель частичного динамического равновесия – паутинообразная модель.
- •59. Источники и движущие силы экономического развития. Критерии экономического развития.
- •60. Сущность, функции и структура рынка.
- •61. Экономическое содержание собственности.
- •62. Закономерности возникновения и развития экономики смешанного типа.
- •63. Законы товарно-денежного обращения
- •64. Модель равновесия «Доходы-Расходы»
- •66. Денежно-кредитная политика в переходной экономике
- •68. Предпринимательство и его сущность. Организационно-правовые формы.
- •69. Акционерный капитал и фондовые биржи.
- •92. Общая характеристика и состав электронного офиса.
- •Предельный доход и спрос (случай линейной функции спроса).Предположим, что кривая спроса монополиста не только имеет отрицательный наклон, но также линейна, как это представлено на рис. 5.2.
- •72. Цена и объем производства фирмы в условиях монополистической конкуренции
- •73. Инфляция: сущность, причины и последствия.
- •73A. Сущность и цели общественного производства.
- •78. Закон спроса и предложения. Состояние рыночного равновесия и его виды.
- •74. Информационные страдства в организации автоматизированных банковских систем.
- •89. Информационные системы в бухгалтерском учете.
- •75. Внемашинное и внутримашинное информационное обеспечение для создания информационных систем в экономике.
- •76. Программно-математическое обеспечение для организации информационных систем в экономике.
- •79. Понятие, принципы формирования и роль информационной стратегии в информационной логистической системе организации.
- •77. Понятие информационных систем в экономике. Принципы создания.
- •81. Информационная логистика: понятие, объект изучения, содержание.
- •82. Классификация информации по разным признакам. Основные понятия (информационные продукт, информационные услуги и т.Д.)
- •83. Понятие информации. Информация и данные, сообщения. Особенности экономической информации. Качество информации.
- •85. Понятие и развитие информатики. Понятие информатики как науки: предмет и задачи, этапы и направления развития информатики.
- •86. Автоматизированные рабочие места: понятие, классификация. Пример использования.
- •87. Информ-ое обеспечение создания информ-ых систем в анализе хоз-ой деят-ти.
- •90. Информационные технологии, их классификация, организация (структура) и средства реализации. Варианты внедрения ит на предприятии.
- •91. Классификация информации и методы организации работы с документами в рф. Принципы организации документооборота.
- •94. Информатизация общества и технологизация социального пространства
- •95. Особенности технологии и классификация экспертных систем.
- •93. Платежная система в интернете. Необходимые условия реализации платежей через интернет. Классификация платежных систем.
- •38. Обобщенная схема мнк.
- •48. Типы и формы собственности.
- •7. Транспортная задача и методы ее решения.
- •88. Перспективы создания ис в экономике.
13. Задача нелинейного программирования и методы их решения. Теорема Куна-Таккера.
В
задаче нелинейного программирования
(НЛП) требуется найти значение многомерной
переменной х=( ),
минимизирующее целевую функцию f(x)
при условиях, когда на переменную х
наложены ограничения типа неравенств
),
минимизирующее целевую функцию f(x)
при условиях, когда на переменную х
наложены ограничения типа неравенств
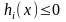 , i=1,2,
(1), а переменные
, i=1,2,
(1), а переменные
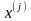 ,
т.е. компоненты вектора х, неотрицательны:
,
т.е. компоненты вектора х, неотрицательны:
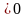 (2).
Рассмотрим общую задачу оптимизации,
содержащую несколько ограничений
в виде равенств:
(2).
Рассмотрим общую задачу оптимизации,
содержащую несколько ограничений
в виде равенств: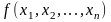
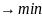 ,
при ограничениях:
,
при ограничениях: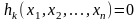 , k=1,..,n.
Эта задача в принципе может быть решена
как задача безусловной оптимизации,
полученная путем исключения из целевой
функции k
независимых
переменных с помощью заданных равенств.
Наличие ограничений в виде равенств
фактически позволяет уменьшить
размерность
исходной задачи
с n
до n-k.
Метод исключения
переменных применим
лишь в тех случаях, когда уравнения,
представляющие ограничения, можно
разрешить относительно некоторого
конкретного набора независимых
переменных. При наличии большого
числа ограничений в виде равенств,
процесс исключения переменных становится
весьма трудоемкой процедурой. С помощью
метода множителей Лагранжа по существу
устанавливаются необходимые условия,
позволяющие идентифицировать точки
оптимума в задачах оптимизации с
ограничениями в виде равенств. При
этом задача с ограничениями преобразуется
в эквивалентную задачу безусловной
оптимизации, в которой фигурируют
некоторые неизвестные параметры,
называемые множителями
Лагранжа.
Рассмотрим задачу минимизации функции
n
переменных с учетом одного ограничения
в виде равенства:
(3), при ограничениях:
, k=1,..,n.
Эта задача в принципе может быть решена
как задача безусловной оптимизации,
полученная путем исключения из целевой
функции k
независимых
переменных с помощью заданных равенств.
Наличие ограничений в виде равенств
фактически позволяет уменьшить
размерность
исходной задачи
с n
до n-k.
Метод исключения
переменных применим
лишь в тех случаях, когда уравнения,
представляющие ограничения, можно
разрешить относительно некоторого
конкретного набора независимых
переменных. При наличии большого
числа ограничений в виде равенств,
процесс исключения переменных становится
весьма трудоемкой процедурой. С помощью
метода множителей Лагранжа по существу
устанавливаются необходимые условия,
позволяющие идентифицировать точки
оптимума в задачах оптимизации с
ограничениями в виде равенств. При
этом задача с ограничениями преобразуется
в эквивалентную задачу безусловной
оптимизации, в которой фигурируют
некоторые неизвестные параметры,
называемые множителями
Лагранжа.
Рассмотрим задачу минимизации функции
n
переменных с учетом одного ограничения
в виде равенства:
(3), при ограничениях: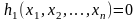 (4). В соответствии с методом множителей
Лагранжа эта задача преобразуется в
следующую задачу безусловной оптимизации:
L(x,u)=f(x)-u*h(x)
(5). Функция
L(х;u)
называется
функцией
Лагранжа, u
— неизвестная
постоянная, которая носит название
множителя
Лагранжа. Множители
Лагранжа можно использовать при
построении критериев оптимальности
для задач оптимизации с ограничениями
в виде равенств. Кун и Таккер обобщили
этот подход на случай общей задачи
нелинейного программирования с
ограничениями, как в виде равенств, так
и в виде неравенств.Рассмотрим следующую
общую задачу нелинейного
программирования:
(4). В соответствии с методом множителей
Лагранжа эта задача преобразуется в
следующую задачу безусловной оптимизации:
L(x,u)=f(x)-u*h(x)
(5). Функция
L(х;u)
называется
функцией
Лагранжа, u
— неизвестная
постоянная, которая носит название
множителя
Лагранжа. Множители
Лагранжа можно использовать при
построении критериев оптимальности
для задач оптимизации с ограничениями
в виде равенств. Кун и Таккер обобщили
этот подход на случай общей задачи
нелинейного программирования с
ограничениями, как в виде равенств, так
и в виде неравенств.Рассмотрим следующую
общую задачу нелинейного
программирования:
 (0), при
ограничениях:
(0), при
ограничениях: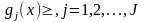 (1)
(1)
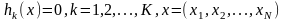 (2). Определение:
Ограничение
в виде неравенства
(2). Определение:
Ограничение
в виде неравенства
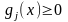 называется активным,
или связывающим, в
точке
называется активным,
или связывающим, в
точке
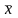 ,
если
,
если
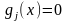 ,
и неактивным,
или несвязывающим, если
,
и неактивным,
или несвязывающим, если
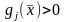 .
Кун и Таккер
построили необходимые и достаточные
условия оптимальности для задач
нелинейного программирования, исходя
из предположения о дифференцируемости
функций
.
Кун и Таккер
построили необходимые и достаточные
условия оптимальности для задач
нелинейного программирования, исходя
из предположения о дифференцируемости
функций
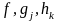 .
Эти условия
оптимальности, широко известные как
условия
Куна—Таккера,
можно
сформулировать в виде задачи
нахождения решения некоторой системы
нелинейных уравнений и неравенств,
или, как иногда говорят, задачи
Куна—Таккера.
Найти векторы
.
Эти условия
оптимальности, широко известные как
условия
Куна—Таккера,
можно
сформулировать в виде задачи
нахождения решения некоторой системы
нелинейных уравнений и неравенств,
или, как иногда говорят, задачи
Куна—Таккера.
Найти векторы
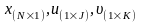 ,
удовлетворяющие следующим условиям
,
удовлетворяющие следующим условиям
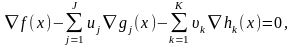 (3)
(3)
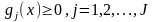 (4)
(4)
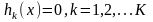 (5)
(5)
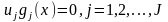 (6)
(6)
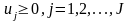 (7).
Для того чтобы интерпретировать условия
Куна — Таккера, рассмотрим задачу
нелинейного
программирования с ограничениями
в виде равенств:
,
при ограничениях:
(7).
Для того чтобы интерпретировать условия
Куна — Таккера, рассмотрим задачу
нелинейного
программирования с ограничениями
в виде равенств:
,
при ограничениях: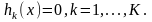 Запишем
условия Куна—Таккера:
Запишем
условия Куна—Таккера:
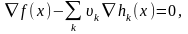 (8)
(8)
![]() (9).
Далее рассмотрим функцию Лагранжа для
задачи нелинейного программирования
с ограничениями в виде равенств:
(9).
Далее рассмотрим функцию Лагранжа для
задачи нелинейного программирования
с ограничениями в виде равенств:
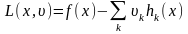 Для этой функции условия оптимальности
первого порядка записываются в виде:
Для этой функции условия оптимальности
первого порядка записываются в виде:
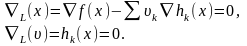 Рассмотрим
задачу
нелинейного программирования с
ограничениями в виде
неравенств:
,
при ограничениях
Рассмотрим
задачу
нелинейного программирования с
ограничениями в виде
неравенств:
,
при ограничениях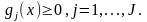 Запишем
условия Куна—Таккера:
Запишем
условия Куна—Таккера: Соответствующая
функция Лагранжа имеет вид:
Соответствующая
функция Лагранжа имеет вид: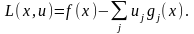 Условия оптимальности
первого порядка записываются как
Условия оптимальности
первого порядка записываются как
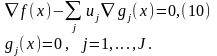 Теорема
1. Необходимость условий Куна—Таккера.
Рассмотрим задачу нелинейного
программирования (0)-(2). Пусть
Теорема
1. Необходимость условий Куна—Таккера.
Рассмотрим задачу нелинейного
программирования (0)-(2). Пусть
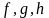 -
дифференцируемые функции, а х*
— допустимое
решение данной задачи. Положим
-
дифференцируемые функции, а х*
— допустимое
решение данной задачи. Положим
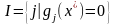 .
Далее пусть
.
Далее пусть
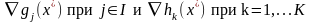 линейно независимы. Если х*
— оптимальное
решение задачи нелинейного
программирования, то существует
такая пара векторов
линейно независимы. Если х*
— оптимальное
решение задачи нелинейного
программирования, то существует
такая пара векторов
 ,
что
является
решением задачи Куна—Таккера (3)—(7).
Условие, согласно которому
должны
быть линейно независимыми, известно
как условие
линейной независимости и
по существу представляет собой некоторое
условие регулярности допустимой
области, которое почти всегда
выполняется для встречающихся на
практике задач оптимизации. Однако
вообще проверка выполнения условия
линейной независимости весьма
затруднительна, так как требуется,
чтобы оптимальное решение задачи было
известно заранее. Вместе с тем условие
линейной независимости всегда выполняется
для задач нелинейного программирования,
обладающих следующими свойствами.
1. Все ограничения в виде равенств и
неравенств содержат линейные функции.
2. Все ограничения
в виде неравенств содержат вогнутые
функции, все ограничения-равенства
— линейные функции, а также существует,
по крайней мере, одна допустимая точка
х, которая расположена во внутренней
части области, определяемой
ограничениями-неравенствами. Другими
словами, существует такая точка х, что
,
что
является
решением задачи Куна—Таккера (3)—(7).
Условие, согласно которому
должны
быть линейно независимыми, известно
как условие
линейной независимости и
по существу представляет собой некоторое
условие регулярности допустимой
области, которое почти всегда
выполняется для встречающихся на
практике задач оптимизации. Однако
вообще проверка выполнения условия
линейной независимости весьма
затруднительна, так как требуется,
чтобы оптимальное решение задачи было
известно заранее. Вместе с тем условие
линейной независимости всегда выполняется
для задач нелинейного программирования,
обладающих следующими свойствами.
1. Все ограничения в виде равенств и
неравенств содержат линейные функции.
2. Все ограничения
в виде неравенств содержат вогнутые
функции, все ограничения-равенства
— линейные функции, а также существует,
по крайней мере, одна допустимая точка
х, которая расположена во внутренней
части области, определяемой
ограничениями-неравенствами. Другими
словами, существует такая точка х, что
 Если
условие линейной независимости в точке
оптимума не выполняется, то задача
Куна—Таккера может не иметь решения.
Теорема о необходимости условий
Куна—Таккера позволяет идентифицировать
неоптимальные точки. Другими словами,
теорему 1 можно использовать для
доказательства того, что заданная
допустимая точка, удовлетворяющая
условию линейной независимости, не
является оптимальной, если она не
удовлетворяет условиям Куна—Таккера.
С другой стороны, если в этой точке
условия Куна—Таккера выполняются, то
нет гарантии, что найдено оптимальное
решение нелинейной задачи. В качестве
примера рассмотрим следующую задачу
нелинейного программирования. Следующая
теорема устанавливает условия, при
выполнении которых точка Куна—Таккера
автоматически соответствует оптимальному
решению задачи нелинейного программирования.
Теорема.2 Достаточность условий
Куна—Таккера. Рассмотрим задачу
нелинейного программирования (0) — (2).
Пусть целевая функция
выпуклая,
Если
условие линейной независимости в точке
оптимума не выполняется, то задача
Куна—Таккера может не иметь решения.
Теорема о необходимости условий
Куна—Таккера позволяет идентифицировать
неоптимальные точки. Другими словами,
теорему 1 можно использовать для
доказательства того, что заданная
допустимая точка, удовлетворяющая
условию линейной независимости, не
является оптимальной, если она не
удовлетворяет условиям Куна—Таккера.
С другой стороны, если в этой точке
условия Куна—Таккера выполняются, то
нет гарантии, что найдено оптимальное
решение нелинейной задачи. В качестве
примера рассмотрим следующую задачу
нелинейного программирования. Следующая
теорема устанавливает условия, при
выполнении которых точка Куна—Таккера
автоматически соответствует оптимальному
решению задачи нелинейного программирования.
Теорема.2 Достаточность условий
Куна—Таккера. Рассмотрим задачу
нелинейного программирования (0) — (2).
Пусть целевая функция
выпуклая,
