
- •1. Типы структурных экономических моделей.Проблемы идентификации и оценивания параметров.
- •6.Статистические оценки и их характеристика.
- •11. Нуль-гипотеза и принцип ее проверки.
- •12.Модель экономического роста Солоу.
- •13. Задача нелинейного программирования и методы их решения. Теорема Куна-Таккера.
- •14. Классификация методов прогнозирования.
- •25. Относительные величины и их значение в статистике. Виды относительных величин и формы их выражения.
- •15. Кибернетический подход в логистике.
- •16. Игры двух лиц с нулевой суммой. Смешанные стратегии. Теорема Неймана. Аналитическое решение игры (2х2).
- •27. Таблица межотраслевого баланса. Основные балансовые соотношения.
- •17. Неоклассическая задача потребления.
- •18. Временные ряды. Их основные характеристики и процедуры сглаживания.
- •23. Производственная функция. Свойства производственных функций. Основные типы производственных функций.
- •28. Тест Дарбина-Уотсона на автокорреляцию по времени.
- •32.Показатели качества регрессии. Коэффициенты корреляции, детерминации, дисперсионное отношение Фишера, стандартные ошибки.
- •35. Задачи линейного программирования. Различные формы записи. Способ решения. Примеры задач.
- •33. Динамический межотраслевой баланс
- •34. Линейная регрессия в условиях мультиколлинеарности. Ридж-оценивание.
- •43. Модель сетевого планирования. Методы срн и pert.
- •47. Основные макроэкономические показатели.
- •49. Предмет и функции «Экономической теории»
- •80. Цель и роль информационных потоков в логистических системах. Структура инф-ной логистич системы как совокупности подсистем для функциональных областей логистики.
- •51. Рынок труда и безработица.
- •52. Совокупный спрос и совокупное предложение
- •55. Предпринимательский доход и экономическая прибыль. Источники экономической прибыли. Функции прибыли.
- •56. Заработная плата: сущность и факторы, ее определяющие. Зарплата в условиях конкурентного рынка.
- •57. Классификация рыночных структур: признаки совершенной конкуренции, монополистической конкуренции и чистой монополии.
- •58. Определение цены и объема производства в условиях чистой монополии (в двух временных периодах).
- •39.Модель частичного динамического равновесия – паутинообразная модель.
- •59. Источники и движущие силы экономического развития. Критерии экономического развития.
- •60. Сущность, функции и структура рынка.
- •61. Экономическое содержание собственности.
- •62. Закономерности возникновения и развития экономики смешанного типа.
- •63. Законы товарно-денежного обращения
- •64. Модель равновесия «Доходы-Расходы»
- •66. Денежно-кредитная политика в переходной экономике
- •68. Предпринимательство и его сущность. Организационно-правовые формы.
- •69. Акционерный капитал и фондовые биржи.
- •92. Общая характеристика и состав электронного офиса.
- •Предельный доход и спрос (случай линейной функции спроса).Предположим, что кривая спроса монополиста не только имеет отрицательный наклон, но также линейна, как это представлено на рис. 5.2.
- •72. Цена и объем производства фирмы в условиях монополистической конкуренции
- •73. Инфляция: сущность, причины и последствия.
- •73A. Сущность и цели общественного производства.
- •78. Закон спроса и предложения. Состояние рыночного равновесия и его виды.
- •74. Информационные страдства в организации автоматизированных банковских систем.
- •89. Информационные системы в бухгалтерском учете.
- •75. Внемашинное и внутримашинное информационное обеспечение для создания информационных систем в экономике.
- •76. Программно-математическое обеспечение для организации информационных систем в экономике.
- •79. Понятие, принципы формирования и роль информационной стратегии в информационной логистической системе организации.
- •77. Понятие информационных систем в экономике. Принципы создания.
- •81. Информационная логистика: понятие, объект изучения, содержание.
- •82. Классификация информации по разным признакам. Основные понятия (информационные продукт, информационные услуги и т.Д.)
- •83. Понятие информации. Информация и данные, сообщения. Особенности экономической информации. Качество информации.
- •85. Понятие и развитие информатики. Понятие информатики как науки: предмет и задачи, этапы и направления развития информатики.
- •86. Автоматизированные рабочие места: понятие, классификация. Пример использования.
- •87. Информ-ое обеспечение создания информ-ых систем в анализе хоз-ой деят-ти.
- •90. Информационные технологии, их классификация, организация (структура) и средства реализации. Варианты внедрения ит на предприятии.
- •91. Классификация информации и методы организации работы с документами в рф. Принципы организации документооборота.
- •94. Информатизация общества и технологизация социального пространства
- •95. Особенности технологии и классификация экспертных систем.
- •93. Платежная система в интернете. Необходимые условия реализации платежей через интернет. Классификация платежных систем.
- •38. Обобщенная схема мнк.
- •48. Типы и формы собственности.
- •7. Транспортная задача и методы ее решения.
- •88. Перспективы создания ис в экономике.
35. Задачи линейного программирования. Различные формы записи. Способ решения. Примеры задач.
Под
задачей линейного программирования
(ЗЛП) понимается задача нахождения в
векторном пространстве
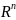 такого вектора x*,
который обеспечивает оптимальное
(максимальное или минимальное значение
линейной функции
такого вектора x*,
который обеспечивает оптимальное
(максимальное или минимальное значение
линейной функции
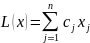 и при этом принадлежит векторной
области, заданной линейными ограничениями
и при этом принадлежит векторной
области, заданной линейными ограничениями
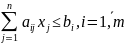
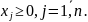 Функцию L(x)
называют целевой функцией ЗЛП, ее
оптимальное значение обозначают L*.
Множество ограничений называют
допустимым множеством, его элементы
– допустимыми веторами, а вектор x*
- решением задачи (оптимальной точкой).
Часто для удобства исследования и при
построении метода решения фиксируется
та или иная запись задачи. Так, часто
используется задача в следующей форме:
Функцию L(x)
называют целевой функцией ЗЛП, ее
оптимальное значение обозначают L*.
Множество ограничений называют
допустимым множеством, его элементы
– допустимыми веторами, а вектор x*
- решением задачи (оптимальной точкой).
Часто для удобства исследования и при
построении метода решения фиксируется
та или иная запись задачи. Так, часто
используется задача в следующей форме:
 Такая
форма записи называется стандартной
или симметричной. Кроме того выделяют
каноническую форму записи:
Такая
форма записи называется стандартной
или симметричной. Кроме того выделяют
каноническую форму записи:
 Вне зависимости от того, как записана
исходная задача, она может быть переписана
в любой желательной форме.
Вне зависимости от того, как записана
исходная задача, она может быть переписана
в любой желательной форме.
.
33. Динамический межотраслевой баланс
Существуют
различные типы динамических моделей.
Все они довольно сложны и различаются
в основном по способу описания взаимосвязи
инвестиций с динамикой объемов
производства. Особую группу составляют
магистральные модели. Они позволяют
рассчитывать оптимальные траектории
экономического роста (магистрали).
Критерии оптимальности, а также
предпосылки и допущения, при которых
формулируются модели, могут быть
разными. Рассмотрим магистральную
модель равновесного роста, предложенную
американским математиком Дж. Фон
Нейманом. Она называется равновесной
потому, что моделирует процесс развития
экономики в предположении, что пропорции
потребления и инвестиций постоянны.
Будем рассматривать развитие экономической
системы в дискретном времени (по годам)
 ,
Где
,
Где
 - вектор валового производства;
- вектор валового производства;
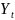 -
соответствующий конечный продукт;
-
соответствующий конечный продукт;
 -вектор
инвестиций;
-вектор
инвестиций;
 -
вектор потребления. Пусть известен
вектор
-
вектор потребления. Пусть известен
вектор
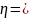 ,
определяющий сложившуюся структуру
потребления. Будем считать его постоянным.
Тогда
,
определяющий сложившуюся структуру
потребления. Будем считать его постоянным.
Тогда
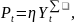 где
где
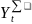 -
суммарный конечный продукт. Для его
определения можно воспользоваться
тем, что суммарный конечный продукт
равен суммарной условно-чистой продукции:
-
суммарный конечный продукт. Для его
определения можно воспользоваться
тем, что суммарный конечный продукт
равен суммарной условно-чистой продукции:
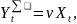 где
где
 вектор
относительно условно-чистой продукции.
Его компоненты определяются по формуле:
вектор
относительно условно-чистой продукции.
Его компоненты определяются по формуле:
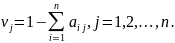 Соотношение, выражающее потребление
как функцию валового производства
Соотношение, выражающее потребление
как функцию валового производства
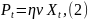 .
Рассмотрим теперь, какова связь между
валовым производством и инвестициями.
Очевидно, что инвестиционный спрос
зависит от желаемого прироста валового
производства
.
Рассмотрим теперь, какова связь между
валовым производством и инвестициями.
Очевидно, что инвестиционный спрос
зависит от желаемого прироста валового
производства
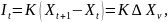
где
K
– матрица коэффициентов капиталоемкости
(приростной фондоемкости). Она
характеризует капитальные затраты,
необходимые для наращивания
производственного потенциала отраслей.
Элемент
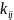 этой матрицы показывает, какое количество
продукции i-ой
отрасли необходимо для того, чтобы за
счет наращивания фондов обеспечить
единичный прирост производства в j-ой
отрасли. В модели предполагается
стабильный, равновесный рост. Если темп
роста обозначить через ,
то
этой матрицы показывает, какое количество
продукции i-ой
отрасли необходимо для того, чтобы за
счет наращивания фондов обеспечить
единичный прирост производства в j-ой
отрасли. В модели предполагается
стабильный, равновесный рост. Если темп
роста обозначить через ,
то
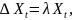 Из этого следует, что
Из этого следует, что
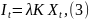 .
Итак, мы выразили две составляющие
конечного продукта через валовое
производство. Подставляя (2) и (3) в (1),
получаем
.
Итак, мы выразили две составляющие
конечного продукта через валовое
производство. Подставляя (2) и (3) в (1),
получаем
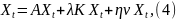 .
Заметим, что в этой модели индекс времени
не играет никакой роли. Так получилось
потому, что модель сформулирована в
предположении, что ситуация в каждом
следующем году структурно повторяет
ситуацию предыдущего года. Опуская
индекс времени и осуществляя простейшие
преобразования из соотношения (4)
получаем
.
Заметим, что в этой модели индекс времени
не играет никакой роли. Так получилось
потому, что модель сформулирована в
предположении, что ситуация в каждом
следующем году структурно повторяет
ситуацию предыдущего года. Опуская
индекс времени и осуществляя простейшие
преобразования из соотношения (4)
получаем
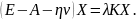 Если предположить, что в матрице
приростной фондоемкости отсутствуют
нулевые строки (в общем случае это
условие не выполняется, поскольку не
все отрасли производят средства
производства), то, умножив обе части
последнего соотношения на
Если предположить, что в матрице
приростной фондоемкости отсутствуют
нулевые строки (в общем случае это
условие не выполняется, поскольку не
все отрасли производят средства
производства), то, умножив обе части
последнего соотношения на
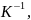 получаем
получаем
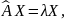 Где
Где
 Таким
образом, расчет параметров равновесного
роста сводится к определению собственных
значений и собственных векторов матрицы
Таким
образом, расчет параметров равновесного
роста сводится к определению собственных
значений и собственных векторов матрицы
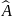 .
В нашем случае множество собственных
значений есть множество возможных
темпов роста. Очевидно, нас интересует
наибольший. Поэтому здесь необходимо
решить не общую, а так называемую частную
задачу, то есть найти наибольшее
собственное значение
.
В нашем случае множество собственных
значений есть множество возможных
темпов роста. Очевидно, нас интересует
наибольший. Поэтому здесь необходимо
решить не общую, а так называемую частную
задачу, то есть найти наибольшее
собственное значение
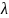 и соответствующий ему вектор Х. Как
известно, собственные векторы находятся
с точностью до постоянного множителя.
Можно так подобрать этот множитель,
что сумма компонентов вектора Х будет
равна 1. В этом случае мы получим
магистраль фон Неймана – пропорции
валового производства, при которых
обеспечивается сложившаяся структура
потребления и достигается наибольший
ежегодный экономический рост. Модель
фон Неймана формулируется при жестких
условиях и предположениях, поэтому
представляет собой сугубо абстрактное
построение. Тем не менее она имеет
важное значение, поскольку дает
теоретическое обоснование того, что
одним из условий интенсивного, устойчивого
развития экономики является оптимизация
пропорций валового производства.
и соответствующий ему вектор Х. Как
известно, собственные векторы находятся
с точностью до постоянного множителя.
Можно так подобрать этот множитель,
что сумма компонентов вектора Х будет
равна 1. В этом случае мы получим
магистраль фон Неймана – пропорции
валового производства, при которых
обеспечивается сложившаяся структура
потребления и достигается наибольший
ежегодный экономический рост. Модель
фон Неймана формулируется при жестких
условиях и предположениях, поэтому
представляет собой сугубо абстрактное
построение. Тем не менее она имеет
важное значение, поскольку дает
теоретическое обоснование того, что
одним из условий интенсивного, устойчивого
развития экономики является оптимизация
пропорций валового производства.
