12 Функция распределения случайной величины и ее свойства.

Функцией распределения случайной величины называют вероятность того, что случайная величина примет частное значение меньшее некоторого фиксированного, т.е.

P(X<x) =F(x).

Геометрически это равенство можно истолковать так: функция распределения F(x) есть вероятность того, что случайная величина X примет значение, которое изображается точкой, лежащей левее точки x.

Так как случайная дискретная величина может принимать значения то функция распределения для нее будет

.

Свойства функции распределения

1) Функция распределения F(x) является неубывающей функцией своего аргумента, т.е. , если .

2) Функция распределения F(x)есть неотрицательная функция, значения которой принадлежат отрезку (0,1), т.е. .

График функции распределения

А) Случайная дискретная величина.

Таблица 2

x	0	1	2
p	0,3	0,5	0,2

F(0 )=0;

F(1)=0,3;

F(2)=P(X=0)+P(X=1)=0,3+0,5=0,8;

F(3)= P(X=0)+P(X=1)+P(X=2)= 0,3+0,5+0,2=1.

Для случайной дискретной величины функция распределения F(x) имеет ступенчатый график (Рис. 2), количество ступенек равно числу частных значений случайной величины, а высота ступеньки равна значению вероятности появления этого частного значения случайной величины.

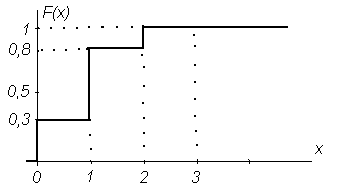
Рисунок 2 График функции распределения случайной дискретной величины

Б) Случайная непрерывная величина.

Функция распределения этой случайной величины представляет собой непрерывную кривую (Рис.3).

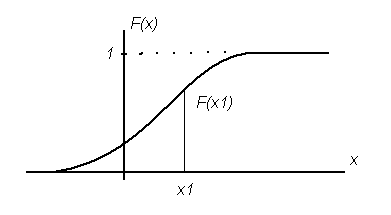
Рисунок 3 График функции распределения случайной непрерывной величины

13 Плотность распределения случайной величины и ее свойства.

Функция распределения случайной непрерывной величины дополнительно обладает еще одним свойством, которое заключается в том, что вероятность того, что случайная непрерывная величина примет одно определенное значение, равна нулю.

Пусть случайная непрерывная величина X может принять частное значение в интервале , причем известна ее функция распределения F(x). Требуется найти вероятность попадания ее в этот интервал, т.е. при условии, что .

Используя предел вероятности попадания величины в заданный интервал, получаем

.

Этот результат означает, что пользоваться формулой (2.1) для определения вероятности попадания случайной непрерывной величины в заданный интервал, близкий нулю, нельзя.

Задание закона распределения не является единственным способом. Очень часто его задают так называемой дифференциальной функцией распределения или плотностью вероятности.

Дифференциальной функцией распределения (плотностью вероятности) f(x) случайной непрерывной величины X называют первую производную от функции распределения случайной непрерывной величины X:

.

Дифференциальная функция f(x) характеризует плотность распределения значений случайной непрерывной величины, что и определило ее второе название.

Действительно, так как вероятность попадания случайной величины X в интервал равна приращению функции на этом интервале, т.е.

,

то отношение этого приращения к приращению аргумента

будет характеризовать среднюю плотность вероятности на этом интервале.

В пределе при стремлении к нулю получим (предполагается, что функция f(x) дифференцируема):

.

График дифференциальной функции f(x) называется кривой распределения.

Установим, как можно найти по известной плотности вероятности f(x):

1) вероятность попадания случайной непрерывной величины в заданный интервал; 2) функцию распределения F(x).

Пусть случайная непрерывная величина X задана плотностью вероятности, график которой изображен на рис. 6.

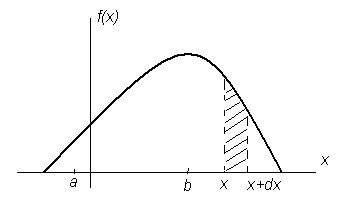
Рисунок 6 График плотности вероятности

Дифференциал функции dF(x)=f(x)dx представляет собой вероятность того, что случайная величина X примет значение в интервале (x, x+ dx).

Произведение f(x)dx называется элементом вероятности. Геометрически это площадь элементарного прямоугольника с основанием dx и высотой f(x).

Для того чтобы найти вероятность попадания случайной величины X в интервал (a, b) по известной плотности вероятности f(x) необходимо просуммировать элементы вероятности f(x)dx в этом интервале:

.

Исходя из определения функции распределения F(x) и последнего выражения, получим

.

Геометрически функции распределения F(x) есть не что иное, как площадь бесконечной фигуры, ограниченной кривой распределения и осью абсцисс, лежащей левее точки x.

Свойства плотности вероятности:

а) плотность вероятности есть функция неотрицательная;

б) распределение имеет размерность обратную размерности случайной величины;

в) интеграл в бесконечных пределах от плотности вероятности равен единице, т.е. .

плотность вероятности применяется только для случайных непрерывных величин.