48 Закон распределения случайной функции.

Под законом распределения случайного процесса понимают всякое соотношение, устанавливающее связь между реализацией случайного процесса и вероятностью ее появления.

Пусть нас интересует реализация случайного процесса x(t), проходящая через точки (таблица 6.1).

Таблица 6.1

t	t0	t1	t2	…	ti	…	tn
x	x0	x0	x2	…	xi	…	xn

Функция называется n – мерной функцией распределения вероятностей случайного процесса и определяется как вероятность того, что случайный процесс X(t) в моменты времени примет значения меньшие соответственно , т.е.

. (6.1)

Если функция имеет смешанную частную производную по аргументам , т.е.

, (6.2)

то она называется n – мерной плотностью вероятности случайного процесса.

Эти функции в зависимости от числа сечений позволяют получить наиболее полное описание случайного процесса. Однако для решения многих инженерных задач достаточно знать одномерный или двумерный закон распределения случайного процесса, т.е. или . Если эти законы имеют нормальное распределение, то и случайный процесс X(t) также называют нормальным.

49 Математическое ожидание и дисперсия случайной функции.

Математическим ожиданием случайного процесса X(t) называется неслучайная функция , которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайного процесса

.

Из определения математического ожидания случайного процесса вытекает, что если известна одномерная плотность вероятности , то

.

Рисунок 6.3 – График функции математического ожидания

Дисперсией случайного процесса X(t) называется неслучайная функция , которая при каждом значении аргумента t равна дисперсии соответствующего сечения случайного процесса.

.

Из определения дисперсии случайного процесса вытекает, что если известна одномерная плотность вероятности , то

или (6.5)

Если случайный процесс представляется в виде , то

. (6.6)

Дисперсия случайного процесса характеризует разброс или рассеивание реализаций относительно функции математического ожидания.

Если реализации случайного процесса представляют собой ток или напряжение, то дисперсию трактуют как разность между мощностью всего процесса и мощностью средней составляющей тока или напряжения в данном сечении, т.е.

. (6.7)

В ряде случаев вместо дисперсии случайного процесса используется среднее квадратичное отклонение случайного процесса

.

Математическое ожидание и дисперсия случайного процесса позволяют выявить вид средней функции, около которой группируются реализации случайного процесса, и оценить их разброс относительно этой функции. Однако внутренняя структура случайного процесса, т.е. характер и степень зависимости (связи) различных сечений процесса между собой, остается при этом неизвестной (рис. 6.4).

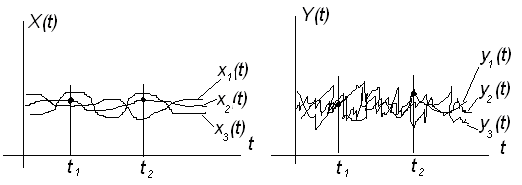
Рисунок 6.4 – Реализации случайных процессов X(t) и Y(t)