39 Теорема сложения дисперсий.
Дисперсия суммы двух случайных величин равна сумме дисперсий и удвоенного корреляционного момента этих величин:
.
(4.5)
Доказательство.
Пусть X+Y=Z, тогда
,
что и требовалось доказать.
Формула (4.2) может быть обобщена на любое число слагаемых:
,
(4.6)
где
-
корреляционный момент случайных величин
,
знак
под суммой обозначает, что суммирование
распространяется на все возможные
парные сочетания случайных величин
.
Если случайные величины не коррелированны, то дисперсия суммы равна сумме дисперсий этих величин:
.
(4.7)
Справедливость
равенства (4.7) вытекает из того, что для
не коррелированных случайных величин
корреляционный момент
.
Дисперсия линейной функции случайных величин равна
,
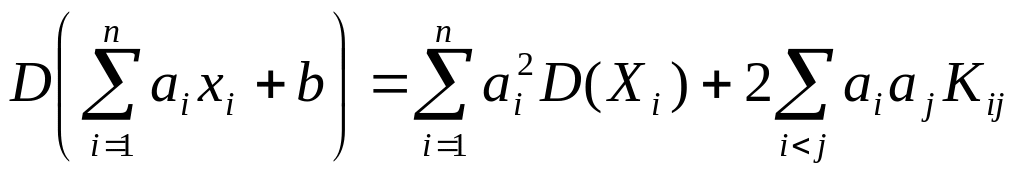(4.8)
где - неслучайные величины.
Если случайные величины не коррелированны, то
.
(4.9)
Пример. Определить дисперсию случайной величины , имеющей комплексный характер.
Дисперсией случайной комплексной величины называют МО квадрата модуля комплексной центрированной случайной величины, поэтому
.
Следовательно, дисперсия
комплексной случайной
величины равна
сумме дисперсий действительной X
и мнимой Y
случайных частей.
Дисперсия произведения двух независимых случайных величин X и Y вычисляется по формуле
.
(4.10)
Доказательство.
Пусть
,
тогда
.
Так как случайные
величины X
и
Y
независимы,
то
и
также
будут независимы, поэтому
.
Кроме того,
.
Следовательно,
,
что и требовалось доказать.
Дисперсия нелинейной функции случайных аргументов. Пусть случайная величина Z является функцией случайных аргументов . Требуется определить дисперсию D(Z).
В общем случае при решении этой задачи нелинейную функцию в окрестности точки линеаризуют разложением ее в ряд Тейлора:
. Применяя к этой случайной величине свойство дисперсии линейной функции и, учитывая, что дисперсия первого слагаемого (детерминированная функция) в этом выражении равна нулю, находим:
.
40 Математическое ожидание линейной функции случайных аргументов.
Функция случайного аргумента X задана законом .
Пусть необходимо определить математическое ожидание этой
функции, если известен закон распределения аргумента.
1. Пусть аргумент Х является дискретной случайной величиной с возможными значениями x1, х2,..., хn, вероятности которых соответственно равны pl, p2, …, рn.
Ясно, что Y также является дискретной случайной величиной с возможными значениями y1 = ϕ(x1), y2 = ϕ(x2), ... , yn = ϕ(xn). Известно, что событие «величина X приняла значение xi означает, что событие «величина Y приняла значение ϕ(xi). В связи с этим можно говорить, что вероятности возможных значений Y соответственно равны pl, p2, ..., рn. Таким образом, математическое ожидание функции равно:
2. Допустим, аргумент X является непрерывной случайной величиной, которая задана плотностью распределения f(x). Чтобы найти математическое ожидание функции Y = ϕ( X ), для начала
можно отыскать плотность распределения g(y) величины Y, а потом применить формулу