24 Эмпирическая функция распределения, ее построение по опытным данным.

Эмпирическую функцию распределения также как статистическое распределение выборки и полигон применяют для изображения дискретного вариационного ряда. Эмпирической функцией распределения называют отношение числа вариант, значения которых меньше некоторого фиксированного значения варианта, к объему выборки, т.е.

,

где - число вариант, значения которых меньше некоторого фиксированного значения варианта.

Пусть произведено n независимых опытов и по данным выборки сформирован вариационный ряд . Для построения графика эмпирической функции распределения определяют ее значения в точках следующим образом. .

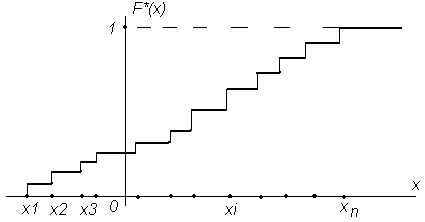
Рис.5.1 – График эмпирической функции распределения

График эмпирической функции распределения (рис.5.1) является случайным. Для уменьшения случайности функции график сглаживают. По этому графику приближенно определяют вид истинной функции распределения случайной величины.

25 Гистограмма частот и относительных частот.

Если выборочные данные относятся к непрерывной случайной величине, то интервал, в котором заключены все наблюдаемые значения, разбивают на частичные интервалы длиной h и находят для каждого частичного интервала сумму частот вариант , попавших в i – й интервал.

Затем строят ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются частичные интервалы длиной и высотой, равной отношению или .

Отношение называют плотностью частоты, а отношение называют плотностью относительной частоты, поэтому и, построенная таким образом, ступенчатая фигура носит название гистограммы частот или гистограммы относительных частот.

Для построения гистограммы частот или относительных частот (рис.5.2) по статистическому распределению выборки необходимо составить таблицу 5.3, в которой отобразить номера и положение частичных интервалов, суммы частот вариант, плотности частот и относительных частот в этих частичных интервалах.

Таблица 5.3

Номер частичного интервала	Частичный интервал	Сумма частот вариант	Плотность частот	Плотность относительных частот
1	1 – 5	10	2.5	0.025
2	5 – 9	20	5	0.05
3	9 – 13	50	12.5	0.125
4	13 – 17	12	3	0.03
5	17 – 21	8	2	0.02

Рисунок 5.2 – Гистограмма частот (а) и относительных частот (б)

Обе гистограммы (рис.5.2) по форме одинаковы и отличаются лишь масштабом по оси ординат. Площадь гистограммы относительных частот, как и площадь плотности распределения случайной величины, равна единице, что позволяет определять вероятность попадания случайной величины в заданный интервал путем вычисления площади части гистограммы, ограниченной этим интервалом.