Вопрос 17. Интегрирование по частям в неопределенном интеграле. Примеры

К числу весьма эффектив­ных методов интегрирования относится метод интегрирования по частям. Этот метод основывается на следующем утвержде­нии.

Пусть каждая из функций и(х) и υ(χ) дифференцируема на множестве {х} и, кроме того, на этом множестве существу­ет первообразная для функции v(x)u'(x). Тогда на множестве {х} существует первообразная и для функции u(x)v'(x), при­чем справедлива формула

(6 .8)

Замечание. Определение дифференциала и свойство инвариантности его формы позволяет записать формулу (6.8) в . виде

(6.9)

Для доказательства сформулированного утверждения запишем формулу для производной произведения двух функций и(х) и υ(χ)

(6.10)

Умножим равенство (6.10) на dx и возьмем интеграл от обеих частей полученного таким путем равенства. Так как по усло­вию для всех х из множества {х} существует и (см. свойство 2° из п. 3 § 1), то для всех х из множества {х} существует и интеграл ,

причем справедлива формула (6.8) (или (6.9)).

Формула (6.9) сводит вопрос о вычислении интеграла к вычислению интеграла В ряде конкретных случаев этот

последний интеграл без труда вычисляется. Вычисление интеграла посредством применения формулы (6.9) и называют интегрированием по частям. Заметим, что при конкретном применении формулы интегрирования по частям (6.9) очень удобно пользоваться таблицей дифференци­алов, выписанной нами в п. 2 § 9 гл. 5.

Переходим к рассмотрению примеров.

1°. Вычислим интеграл . Полагая

и используя формулу (6.9), получим

2°. Вычислим далее интеграл Полагая и =

=arctgx:, dv = х dx и используя формулу (6.9), будем иметь

3°. Вычислим интеграл Сначала применим

формулу (6.9), полагая Получим Для вычисления последнего интеграла еще раз применим формулу (6.9), полагая на этот раз и = x, dv = sin x dx. Получим du = dx, υ = — cos x,

Таким образом, интеграл вычислен нами посредством двукратного интегрирования по частям. Легко понять, что интеграл (где п — любое целое положительное число) может быть вычислен по аналогичной схеме посредством n-кратного интегрирования по частям.

Интегрирование по частям - приём, который применяется почти так же часто, как и замена переменной. Пусть u(x) и v(x) - функции, имеющие непрерывные частные производные. Тогда по формуле дифференцирования произведения d(uv) = u∙dv + v∙du . Находим неопределённые интегралы для обеих частей этого равенства (при этом ): . Эта формула и называется формулой интегрирования по частям. Часто ее записывают в производных ( ): . Примеры: .

.

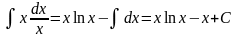Формула интегрирования по частям может применяться неоднократно. При наличии небольшого опыта в простых интегралах нет необходимости выписывать промежуточные выкладки (u = …, dv = …), можно сразу применять формулу, представив интеграл в виде :

.

Вопрос 18. Вычислениe неопределённых интегралов, содержащих в знаменателе квадратный трёхчлен.

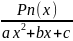∫ dx, где Pn(x) – некоторый многочлен степени x.

= Q_n-2(x)+αx+β

∫ dx = ∫Q_n-2(x)dx+∫ dx =

первый вычисляется как сумма.

считаем второй:

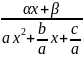∫ dx = ∫ = ∫ dx =

= ∫ dx = ∫ dx+ ∫

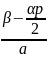I₁=∫ dx = ∫ dx = ∫ = ln|t|+C = ln| |+C

q-p²/4= d²

I₂= ∫ = ∫ = ∫ = ∫ =

= а) +C , если знак + ; б) ln| |+C, если знак “-“

Замечание: используя те же приёмы, можно считать интегралы такого вида:

∫ = ∫ = длинный ln ( =q-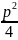 )