
- •Вопрос 1 Предел последовательности. Ограниченные, возрастающие, убывающие последовательности.
- •Вопрос 2 Предел функции.
- •Вопрос 3. Замечательные пределы.
- •Вопрос 4. Непрерывные функции
- •Вопрос 5 .Определение производной. Примеры.
- •Вопрос 6. Таблица производных.
- •Вопрос 7. Основные правила дифференцирования.
- •Вопрос 8. Производные и дифференциалы высших порядков.
- •Вопрос 9.Правило Лопиталя.
- •Вопрос 10. Возрастание и убывание функции.
- •Вопрос11 Точки экстремума функции. Необходимые условия экстремума.
- •Вопрос 12. Выпуклость и вогнутость.
- •Вопрос 13. Общая схема построения графика функции.
- •Вопрос14 Первообразная функция. Структура множества первообразных функций
- •Вопрос 15. Неопределенный интеграл его свойства. Таблица интегралов
- •Вопрос 16. Замена переменной в неопределенном интеграле.Примеры.
- •Вопрос 17. Интегрирование по частям в неопределенном интеграле. Примеры
- •Вопрос 18. Вычислениe неопределённых интегралов, содержащих в знаменателе квадратный трёхчлен.
- •Вопрос 19. Итегрирование рациональных дробей
- •Вопрос 20. Разложение рациональной дроби на простейшие.
- •Вопрос21 Интегрирование иррациональных выраж. Дробно- линейные иррациональности.
- •Вопрос22. Интегрирование тригонометрических выражений.
- •Вопрос 23. Определенный интеграл. Необходимое условие интегрируемости.
- •Вопрос 24. Определение и геометрический смысл определенного интеграла
- •Вопрос25 Свойства определенного интеграла
- •Вопрос 26. Приложение определенного интеграла. Вычисление площади криволинейной трапеции.
- •Вопрос 27. Теорема о замене переменной в определенном интеграле.
- •Вопрос 28. Несобственные интегралы.
- •Вопрос 29. Понятие диф ур-я, основные определения.
- •Вопрос 30, Задача Коши для диф. Ур 1пор.
- •Вопрос 31. Дифференциальные уравнения с разделенными переменными
- •Вопрос 32. Диф. Уравнения с разделяющимися пер-ми.
- •Вопрос 33. Диф. Однородные диф. Ур-я 1-го порядка.
- •Вопрос34. Лин диф ур.
- •Вопрос 36.Интегрируемые типы диф ур-й 2-го порядка
- •Вопрос 37. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- •Вопрос 38. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
- •Вопрос 39. Комплексные числа.
- •Вопрос 40. Функции нескольких переменных. Основные определения и свойства.
- •Вопрос 41. Производные от функций многих переменных.
- •Вопрос 42. Исследование функций двух независимых переменных на экстремум
- •Вопрос 43. . Числовые ряды. Основные понятия.
- •Вопрос 44. Признак сравнения.
- •Вопрос 45. Знакочеред ряды. Т Лейбница.
- •Теор Признак Лейбница
- •Вопрос 47. Разложение элементарных функций в ряд Маклорена
- •Вопрос 48. Интегрирование дифференциальных уравнений с помощью степенных рядов.
- •Вопрос 49. Решение дифференциальных уравнений с помощью степенных рядов.
- •Вопрос 50. Множества. Операции над множествами
Вопрос 15. Неопределенный интеграл его свойства. Таблица интегралов
Определение. Совокупность всех первообразных функций для данной функции f(x) на интервале (а,b) называется н е-опреде ленным интегралом от функции f(x)
(на
этом интервале) и обозначается символом![]()
(6.1)
В этом обозначении знак ѓ называется знаком интеграла, выражение f(x) dx ~ подынтегральным выражением, а сама функция f(x) — подынтегральной функцией.
Если F(x) — одна из первообразных функций для функции f(x) на интервале (а, b), то, в силу следствия из теоремы 6.1,
![]() (6.2)
(6.2)
где С — любая постоянная.
Подчеркнем, что если первообразная (а стало быть, и неопределенный интеграл) для функции f(x) на интервале (а,b) существует, то подынтегральное выражение в формуле (6.1) представляет собой дифференциал любой из этих первообразных. В самом деле, пусть F(x) — любая из первообразных для функции f(x) на интервале (а,b), т.е. для всех х из интервала (a,b) F'{x) = f(x). Тогда f(x)dx = F'(x)dx = dF
Основные свойства неопределенного интеграла.
Прежде всего отметим два свойства, непосредственно вытекающие из определения неопределенного интеграла:
![]()
Свойство 1° означает, что знаки d и (интеграл) взаимно сокращаются в случае, если знак дифференциала стоит перед знаком интеграла.
Свойство 2° означает, что знаки ѓ и d взаимно сокращаются и в случае, если знак интеграла стоит перед знаком дифференциала, но в этом случае к F(x) следует добавить произвольную постоянную С.
Для установления свойства 1° достаточно взять дифференциал от обеих частей формулы (6.2) и учесть, что dF{x) = = F'(x)dx = f(x)dx.
Для установления свойства 2° достаточно в левой части (6.2) воспользоваться равенством dF(x) = f(x) dx.
Следующие два свойства обычно называют линейными свойствами интеграла:

![]()
Неопределённый интеграл и его свойства.
Множество всех первообразных функции называется неопределённым интегралом.
Свойства:
1. Интеграл суммы равен сумме интегралов.
2. ∫аf(x)dx=a∫f(x)dx
3. Если ∫f(x)dx=F(x)+C то ∫f(αx)dx=1/αF(αx)+C
4. Если ∫f(x)dx=F(x)+C то ∫F(x+B)dx=F(x+B)+C
5. объединённые 3 и 4
Таблица основных интегралов.
1)
∫ xdx
=
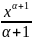 +C
+C
2)
∫
 dx
= ln|x|+C
dx
= ln|x|+C
3)
∫ axdx
=
 +C
+C
4) ∫ exdx = ex+C
5) ∫ sinxdx = -cosx+C
6) ∫ cosxdx = sinx+C
7)
∫
 dx
= tgx+C
dx
= tgx+C
8)
∫
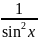 dx
= -ctgx+C
dx
= -ctgx+C
9)
∫
 dx
= arctgx+C
dx
= arctgx+C
10)
∫
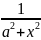 dx
=
dx
=
 arctg
arctg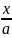 +C
+C
Док-во:
∫
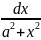 =
=
 ∫
∫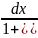
(a-arctg )+C = arctg +C
11)
∫
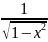 dx
= arcsinx+C
dx
= arcsinx+C
12)
∫
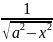 dx
= arcsin
+C
dx
= arcsin
+C
13)
∫
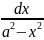 =?
=?
Применяем приём разложения дроби на простейшие:
 =
=
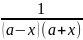 =
=
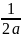 (
( )
=>
)
=>
=>
∫
=
(∫ dx
+ ∫
dx
+ ∫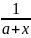 dx)
=
dx)
=
=
(-ln|a-x|+ln|a+x|+C)
=
ln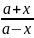 +C
+C
Это интеграл «короткий логарифм»
14)
∫
 = ln(x
= ln(x )+C
)+C
«длинный логарифм»
Опр.Множество
первообразных функции f(x)
называется неопределённым интегралом
от этой функции и обозначается символом
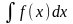 .
Как следует из изложенного выше, если
F(x)
- некоторая первообразная функции f(x),
то
.
Как следует из изложенного выше, если
F(x)
- некоторая первообразная функции f(x),
то
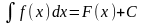 ,
где C
- произвольная постоянная. Функцию f(x)
принято называть подынтегральной
функцией, произведение
f(x)
dx
- подынтегральным выражением.
,
где C
- произвольная постоянная. Функцию f(x)
принято называть подынтегральной
функцией, произведение
f(x)
dx
- подынтегральным выражением.
Вопрос 16. Замена переменной в неопределенном интеграле.Примеры.
Пусть
.
Тогда
 .
Здесь t(x)
- дифференцируемая монотонная функция.
.
Здесь t(x)
- дифференцируемая монотонная функция.
Док-во
непосредственно следует из формулы для
производной сложной функции. Перепишем
первый интеграл, заменив переменную x
на t:
 .
Это означает, что
.
Это означает, что
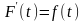 .
Заменим независимую переменную t
на функцию t
= t(x):
.
Заменим независимую переменную t
на функцию t
= t(x):
 .
Следовательно, функция F(t(x))
является первообразной для произведения
.
Следовательно, функция F(t(x))
является первообразной для произведения
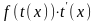 ,
или
.
,
или
.
При решении задач замену переменной можно выполнить двумя способами.
1.
Если в подынтегральной функции удаётся
сразу заметить оба сомножителя, и
f(t(x)),
и
 ,
то замена переменной осуществляется
подведением множителя
под знак дифференциала:
,
то замена переменной осуществляется
подведением множителя
под знак дифференциала:
 ,
и задача сводится к вычислению интеграла
,
и задача сводится к вычислению интеграла
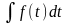 .
Например,
.
Например,
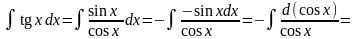 (задача сведена к вычислению
(задача сведена к вычислению
 ,
где t
= cos
x)
,
где t
= cos
x)
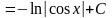 (аналогично
находится интеграл от
(аналогично
находится интеграл от
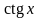 );
);
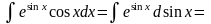 (задача сведена к вычислению
(задача сведена к вычислению
 ,
где t
= sin
x)
,
где t
= sin
x)
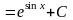 .
.
2.
Замену переменной можно осуществлять
формальным сведением подынтегрального
выражения к новой переменной. Так, в
 имеет смысл перейти к переменной
(сделать подстановку) t
= sin
x.
Выражаем все множители подынтегрального
выражения через переменную t:
имеет смысл перейти к переменной
(сделать подстановку) t
= sin
x.
Выражаем все множители подынтегрального
выражения через переменную t:
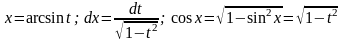 ;
в результате
;
в результате
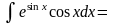
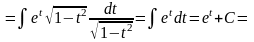 (возвращаемся к исходной переменной)
.
(возвращаемся к исходной переменной)
.
