Вопрос 5 .Определение производной. Примеры.

Если мы имеем точку х на оси, то, чтобы перейти в новую точку, мы даём аргументу приращение Δх (х→Δх). Δу=f(x+Δx)-f(x). Когда х получает приращение Δх, функция y=f(x) получает приращение Δу.

Определение.

Производной функции y=f(x) в точке x называется предел отношения Δу к Δх, когда Δх стремится к 0, если этот предел существует и конечен.

y’(x) = f’(x) = y’ =

= =

Примеры.

1) y=x²

Δy = (x+Δx)²-x² = x²+2xΔx+Δx²-x² = 2xΔx+Δx²

y’ =

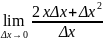= = = 2x+Δx) = 2x

2) y=sinx

Δy=sin(x+Δx)-sin(x)=2sin(Δx/2)*cos(x+Δx/2)

y’= = =

= = = cos(x)

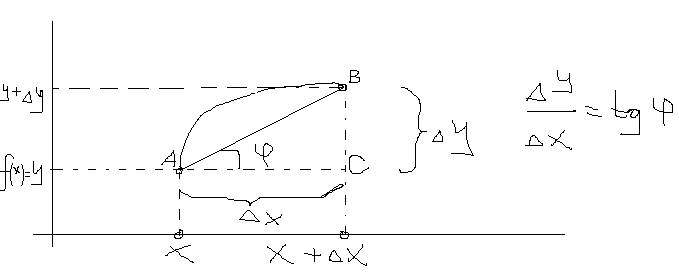
Геометрический смысл производной.

Дана точка x. Рассмотрим приращение (x+Δx)

Δy=f(x+Δx)-f(x)

Производная = = =

= y’ = f’(x)

Если функция имеет в точке производную, она называется дифференцируемой в этой точке.

Пусть Δх → 0, или B→A. Каждый раз будет новая B, новый и новая хорда AB. Очевидно, что, когда B совпадёт с A, хорда совпадёт с касательной, т.е., предельное положение хорды - касательная к графику функции в точке A.

= tg ₀, где фи₀ – угол наклона касательной к оси X. Производная – тангенс угла, образованного касательной с осью X.

Из сказанного выше вытекает, что существование производной в точке x (или, иначе, дифференцируемость функции в точке x) означает, что в этой точке существует касательная к графику функции.

Вопрос 6. Таблица производных.

Вопрос 7. Основные правила дифференцирования.

Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с) ' = 0, (cu) ' = cu';

2) (u+v)' = u'+v';

3) (uv)' = u'v+v'u;

4) (u/v)' = (u'v-v'u)/v^2;

Теорема

Если функции u=u(x) и v=v(x) имеют в точке x производные, то сумма (разность), произведение и частное этих функций также имеют производные в этой точке, и справедливы следующие формулы: 1) (u±v)/=u/±v/, 2) (u·v)/=u/v+v/u, 3) (vu)=v2u/v−v/u .

Доказательство Из определения производной:

(u±v)/=limΔx→0Δx[u(x+Δx)±v(x+Δx)]−[u(x)±v(x)]=limΔx→0Δx[u(x+Δx)−u(x)]±[v(x+Δx)−v(x)]=limΔx→0Δxu(x+Δx)−u(x)±limΔx→0Δxv(x+Δx)−v(x)=u/±v/

(u·v)/=limΔx→0Δxu(x+Δx)·v(x+Δx)−u(x)·v(x)±v(x+Δx)·v(x)= limΔx→0Δxu(x+Δx)[v(x+Δx)−v(x)]+limΔx→0Δxv(x)[u(x+Δx)−u(x)]=uv/+vu/.

(vu)/=limΔx→0Δxv(x+Δx)u(x+Δx)−v(x)u(x)=limΔx→0Δx·v(x+Δx)·v(x)u(x+Δx)·v(x)−u(x)·v(x+Δx)±u(x)·v(x)=v2u/v−v/u. Теорема доказана.

Вопрос 8. Производные и дифференциалы высших порядков.

Пусть y=f(x). Её производная f’(x) меняется от точки к точке и сама является функцией аргумента х. =f’(x), поэтому можно говорить о производной от производной.

Второй производной от функции является производная от производной.

( ) = = f’’(x) = = y’’

Аналогично определяются производные более высокого порядка.

=

И число e, от которого сколько производных не бери, оно всегда будет равняться самому себе. Это замечательное число. Откуда оно взялось – непонятно… Часто так бывает, что формулы умнее того, кто их придумал.

dy=f’(x)*dx

Очевидно, что f’(x)*Δx меняется от точки к точке, => dy можно считать функцией от х

d(dy)=d(f’(x)dx)=(f’(x)dx)’*dx=f’’(x)dxdx=

=f’’(x)dx²=d²y

d³y=f’’’(x)dx³ => fⁿ(x) =