Вопрос 48. Интегрирование дифференциальных уравнений с помощью степенных рядов.

Пусть дана задача Коши: ,

Решение этой задачи в виде ряда Тейлора ищется так. . Первые n коэффициентов ряда известны из начальных условий, остальные находятся последовательным дифференцированием уравнения.

Примеры. 1. . Из уравнения находим . Дифференцируем уравнение: . Далее дифференцируем уравнение и находим значение производной в точке 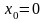: , 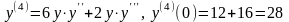. Так мы можем вычислить производные любого порядка. Решение задачи Коши: .

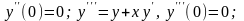
2. . Находим: Закономерность понятна. Производные порядка 3n-1 и 3n равны нулю, производная порядка 3n+1 равна , поэтому. С помощью признака Даламбера легко убедится, что этот ряд сходится при 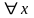, следовательно, даёт решение задачи Коши на всей числовой оси.

Вопрос 49. Решение дифференциальных уравнений с помощью степенных рядов.

С помощью степенных рядов возможно интегрировать дифференциальные уравнения.

Рассмотрим линейное дифференциальное уравнение вида:

Если все коэффициенты и правая часть этого уравнения разлагаются в сходящиеся в некотором интервале степенные ряды, то существует решение этого уравнения в некоторой малой окрестности нулевой точки, удовлетворяющее начальным условиям.

Это решение можно представить степенным рядом:

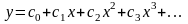
Для нахождения решения остается определить неизвестные постоянные c_i.

Эта задача решается методом сравнения неопределенных коэффициентов. Записанное выражение для искомой функции подставляем в исходное дифференциальное уравнение, выполняя при этом все необходимые действия со степенными рядами (дифференцирование, сложение, вычитание, умножение и пр.)

Затем приравниваем коэффициенты при одинаковых степенях х в левой и правой частях уравнения. В результате с учетом начальных условий получим систему уравнений, из которой последовательно определяем коэффициенты c_i.

Отметим, что этот метод применим и к нелинейным дифференциальным уравнениям.

Пример. Найти решение уравнения c начальными условиями y(0)=1, y’(0)=0.

Решение уравнения будем искать в виде

Подставляем полученные выражения в исходное уравнение:

Отсюда получаем:

Получаем, подставив начальные условия в выражения для искомой функции и ее первой производной:

Окончательно получим:

Итого:

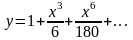
Существует и другой метод решения дифференциальных уравнений с помощью рядов. Он носит название метод последовательного дифференцирования.

Рассмотрим тот же пример. Решение дифференциального уравнения будем искать в виде разложения неизвестной функции в ряд Маклорена.

Если заданные начальные условия y(0)=1, y’(0)=0 подставить в исходное дифференциальное уравнение, получим, что

Далее запишем дифференциальное уравнение в виде 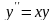и будем последовательно дифференцировать его по х.

После подстановки полученных значений получаем:

Вопрос 50. Множества. Операции над множествами

Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись  a   R  означает, что элемент  а принадлежит множеству R , то есть  а  является элементом множества R . В противном случае, когда  а  не принадлежит множеству  R , пишут  a   R .  

 Два множества А и В называются  равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А  является элементом множества  В  и наоборот, каждый элемент множества  В  является элементом множества  А .

Говорят, что множество А содержится в множестве В ( рис.1 ) или  множество А  является подмножеством множества  В ( в этом случае пишут А   В ), если каждый элемент множества  А одновременно является элементом множества  В . Эта зависимость между множествами называется  включением. Для любого множества  А имеют место включения:      А  и  А   А .

Сумма ( объединение ) множеств  А и В ( пишется  А   В ) есть множество элементов, каждый из которых принадлежит либо А , либо В. Таким образом,  е   А   В  тогда и только тогда, когда либо  е   А ,  либо  е   В .  

Произведение ( пересечение ) множеств  А и В ( пишется  А   В , рис.2 ) есть множество элементов, каждый из которых принадлежит и А , и В . Таким образом,  е   А   В  тогда и только тогда, когда   е   А  и  е   В .

Разность множеств А и В ( пишется  А – В , рис.3 ) есть множество элементов, которые принадлежат множеству А , но не принадлежат множеству В. Это множество называется также дополнением множества В относительно множества А.

Симметричная разность множеств А и В ( пишется  А \ В  ) есть множество: А \ В  = ( А – В )   ( В – А ).

 Свойства операций над множествами: