Вопрос 45. Знакочеред ряды. Т Лейбница.

Ряд у которого полож. члены чередуются через один наз-ся знакочередующимся. Для зн.ч. ряда им-ся свой дост. признак. сх-ти.

Теор Признак Лейбница

Если у зн.ч. ряда n-й член стремится к 0 монотонно убывая, то ряд сх-ся, сумма ряда им. знак 1го члена ряда и не превосх. его по модулю.

 Пусть у зн.ч. ряда a1+a2-…-an+… lim |a_n|=0, |a1||a2||a3||an|=c_n тогда ряд запис. в виде с1-с2+с3-… (1), если a10 и –с1+с2-с3+… (2) если а10.

а10. Для частич. сумм с чёт. номерами n=2k имеем S_2k=c1-c2+c3-c4+…+c_2k-1-c_2k=

{(c1-c2)+(c3-c4)+…+ c_2k-1-c_2k (3)

{c1-(c2-c3)-(c4-c5)-…-c_2k (4). Т.к. с1с2…, то все скобки 0, поэтому (3) S_2k0, посл. {S_2k} возрастает: S_2k+2 = S_2k+ (c_2k+1-c_2k+2) S_2k. (4) S_2kc1. Т.о. {S_2k} возрастает и ограничена сверху она имеет конеч. lim S, причём 0 S_2kс10 Sс1.

Вопрос 46. Степенные ряды. Среди функциональных рядов в математике и ее приложениях особую роль играет ряд, членами которого являются степенные функции аргумента х, т.е. так называемый степенной ряд:  (2.2) Действительные (или комплексные) числа   называются коэффициентами ряда (2.2),  – действительная переменная. Ряд (2.2) разложен по степеням х. Рассматривают также степенной ряд, разложенный по степеням  , т.е. ряд вида , (2.3) где   – некоторое постоянное число. Ряд (2.3) легко приводится к виду (2.2), если положить  . Поэтому при изучении степенных рядов можем ограничиться степенными рядами вида (2. 2). Область сходимости степенного ряда (2.2) содержит по крайней мере одну точку х = 0 (ряд (2.3) сходится в точке  ).

Формулы и ряды Тейлора и Маклорена. Разложение функций в степенные ряды.

Ряды Тейлора и Макларена.

; f(x)=S_n(x)+R_n(x) (6); f(x)-S_n(x)=R_n(x) (6). Потребуем, чтобы функция f(x) имела бесконечное число производных f⁽ⁿ⁾(x) в точке x=а и её окрестности. Получим: lim (f(x)-S_n(x))=lim R_n(x)=0 (7) . Если lim R_n(x) сущ-ет и равен 0, то f(x)=lim S_n(x) (8)  (9) - ряд Тейлора. При а=0 получаем ряд Макларена:

.

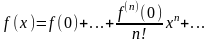Замечание Функция представлена в форме ряда Тейлора в том случае если R_n(x)0.

Пример неразложимости функции в ряд Тейлора.

. Т.к. =0, то функция f(x) непрерывная 

Обозначим . По правилу Лопиталя

Аналогичным образом устанавливается, что функция f(x) имеет бесконечно большое число производных и все они непрерывны на всей оси, включая точку х=0 и в точке х=0 обращаются в нуль.

n=0,1,2... S_n(x)=0. f(x)=S_n(x)+R_n(x)R_n(x)  R_n(x)- не стремится к нулю, то ряда Тейлора для этой функции не сущ-ет.

Вопрос 47. Разложение элементарных функций в ряд Маклорена

Разложить функцию в ряд Маклорена. Найти область сходимости полученного ряда.! Эквивалентная формулировка: Разложить функцию в ряд по степеням   

Конструируем наш ряд. Плясать начинают, как правило, от функции, в данном случае – от косинуса. Используем элементарное разложение:

.  Область сходимости ряда: 

В данном случае 

В числителях раскрываем скобки:

Теперь умножаем обе части на «икс»:

В итоге искомое разложение функции в ряд:

Как определить область сходимости? Разложение косинуса сходится при ЛЮБОМ значении «альфа»:  , а значит и при  . Домножение   на «икс» не играет никакой роли в плане сходимости. Поэтому область сходимости полученного ряда: