Вопрос 43. . Числовые ряды. Основные понятия.

Опр. Сумма членов беск числ посл-сти - числ ряд.

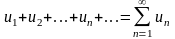Числа -чл ряда, а u_n – общим членом ряда. Опр. Суммы 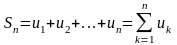, n = 1, 2, … - частн суммы ряда. То, возможно рассм посл-сти частичных сумм ряда S₁, S₂, …,S_n, …

Опр. Ряд - сход-ся, если сх-ся посл-ть его частных сумм. Сумма схо ряда – предел посл-сти его частных сумм. Опр. Если посл-сть частных сумм ряда расхо-я, т.е. не имеет предела, или имеет бескон предел, то ряд –расх-ся и ему не ставят в соответствие никакой суммы. Свойства рядов.1) Схо-сть или расх-сть ряда не нарушится если изменить, отбросить или добавить конечное число членов ряда.

2) Рассмотрим два ряда и , где С – пост число.

Теор. Если ряд сх и его сумма =S, то ряд тоже сходится, и его сумма равна СS. (C  0) 3) Рассмотрим два ряда и 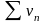. Суммой или разностью этих рядов будет называться ряд , где эл-ты получены в результате сложения (вычитания) исх-х эл-в с одинак номерами. Теор. Если ряды и сходятся и их суммы равны соответственно S и , то ряд тоже сходится и его сумма = S + . Разность 2х сходящихся рядов также будет сходящимся рядом. Сумма сх и расх рядов будет расх рядом. О сумме 2х расх рядов общего утверждения сделать нельзя. При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.

Вопрос 44. Признак сравнения.

Пусть даны два ряда с положительными членами.  и  Причем, каждый член ряда  не превосходит соответствующего члена ряда  , то есть  для всех  . Тогда  

если сходится ряд  с большими членами, то сходится и ряд  с меньшими членами; 

если расходится ряд  с меньшими членами, то расходится и ряд  с большими членами. 

Теорема остается верна, если соотношения между членами рядов выполняются не для всех  , а лишь начиная с некоторого номера  .  

При использовании признаков сравнений чаще всего исследуемый ряд сравнивают с бесконечной геометрической пргрессией  , которая сходится при  и расходится при  , или с рядом  , который сходится при  и расходится при  .  

Признак Даламбера.

Пусть l - предел отношения последующего члена u_n+1 ряда (1) к предыдущему u_n при n , т.е.

Тогда,   если l < 1, то ряд l сходится,   если l > 1, то ряд l расходится,   Если же l = 1, то вопрос о сходимости ряда (1) остается открытым.   Доказательство. Согласно определению предела переменной величины, равенство

означает, что, начиная с некоторого номера n, выполняются неравенства

где e   - наперед заданное сколь угодно малое положительное число.   Рассмотрим три случая:   а) пусть l < 1 . Тогда всегда можно взять e   настолько малым, чтобы выполнялось неравенство

l +   < 1

и, начиная с некоторого n , неравенство

где q = l + , в силу чего (см. теорему 1) ряд (1) будет сходящимся;   б) пусть l > 1 . Выбираем e   так, чтобы

 = l - 1 > 0

  Тогда l -  = 1 и

т.е. ряд (1) расходится (см. теорему 1)   в) пусть l = 1 . Тогда ряд (1) может быть как сходящимся, так и расходящимся.   В самом деле, для гармонического ряда

который расходится, имеем,

  С другой стороны, ряд

сходится, а для него также

Коши радикальная сходимость ряда.

Если для числового ряда с неотрицательными членами существует т число d, 0 < d < 1, что, начиная с некоторого номера, вып нера-во , то данный ряд сходится. Если для ряда

, то если ряд сходится, если l > 1 ряд расходится. Док-во. 1. Пусть l < 1. существует такое , что . Поскольку сущ предел , то подставив в определение предела выбранное получим: Раскрыв модуль, получаем: ; ; Поскольку , то ряд сходится. Следовательно, по признаку сравнения ряд тоже сходится. 2. Пусть l > 1. Очевидно, что существует такое , что . Поскольку существует предел , то подставив в определение предела выбранное получим: Раскрыв модуль, получаем: ;

Поскольку , то ряд расх. След-но, по признаку сравнения ряд тоже расходится.