
- •Вопрос 1 Предел последовательности. Ограниченные, возрастающие, убывающие последовательности.
- •Вопрос 2 Предел функции.
- •Вопрос 3. Замечательные пределы.
- •Вопрос 4. Непрерывные функции
- •Вопрос 5 .Определение производной. Примеры.
- •Вопрос 6. Таблица производных.
- •Вопрос 7. Основные правила дифференцирования.
- •Вопрос 8. Производные и дифференциалы высших порядков.
- •Вопрос 9.Правило Лопиталя.
- •Вопрос 10. Возрастание и убывание функции.
- •Вопрос11 Точки экстремума функции. Необходимые условия экстремума.
- •Вопрос 12. Выпуклость и вогнутость.
- •Вопрос 13. Общая схема построения графика функции.
- •Вопрос14 Первообразная функция. Структура множества первообразных функций
- •Вопрос 15. Неопределенный интеграл его свойства. Таблица интегралов
- •Вопрос 16. Замена переменной в неопределенном интеграле.Примеры.
- •Вопрос 17. Интегрирование по частям в неопределенном интеграле. Примеры
- •Вопрос 18. Вычислениe неопределённых интегралов, содержащих в знаменателе квадратный трёхчлен.
- •Вопрос 19. Итегрирование рациональных дробей
- •Вопрос 20. Разложение рациональной дроби на простейшие.
- •Вопрос21 Интегрирование иррациональных выраж. Дробно- линейные иррациональности.
- •Вопрос22. Интегрирование тригонометрических выражений.
- •Вопрос 23. Определенный интеграл. Необходимое условие интегрируемости.
- •Вопрос 24. Определение и геометрический смысл определенного интеграла
- •Вопрос25 Свойства определенного интеграла
- •Вопрос 26. Приложение определенного интеграла. Вычисление площади криволинейной трапеции.
- •Вопрос 27. Теорема о замене переменной в определенном интеграле.
- •Вопрос 28. Несобственные интегралы.
- •Вопрос 29. Понятие диф ур-я, основные определения.
- •Вопрос 30, Задача Коши для диф. Ур 1пор.
- •Вопрос 31. Дифференциальные уравнения с разделенными переменными
- •Вопрос 32. Диф. Уравнения с разделяющимися пер-ми.
- •Вопрос 33. Диф. Однородные диф. Ур-я 1-го порядка.
- •Вопрос34. Лин диф ур.
- •Вопрос 36.Интегрируемые типы диф ур-й 2-го порядка
- •Вопрос 37. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- •Вопрос 38. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
- •Вопрос 39. Комплексные числа.
- •Вопрос 40. Функции нескольких переменных. Основные определения и свойства.
- •Вопрос 41. Производные от функций многих переменных.
- •Вопрос 42. Исследование функций двух независимых переменных на экстремум
- •Вопрос 43. . Числовые ряды. Основные понятия.
- •Вопрос 44. Признак сравнения.
- •Вопрос 45. Знакочеред ряды. Т Лейбница.
- •Теор Признак Лейбница
- •Вопрос 47. Разложение элементарных функций в ряд Маклорена
- •Вопрос 48. Интегрирование дифференциальных уравнений с помощью степенных рядов.
- •Вопрос 49. Решение дифференциальных уравнений с помощью степенных рядов.
- •Вопрос 50. Множества. Операции над множествами
Вопрос 38. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
Представляется возможным представить вид частного решения в зависимости от вида правой части неоднородного уравнения.
 Различают
следующие случаи:
Различают
следующие случаи:
I. Правая часть линейного неоднородного дифференциального уравнения имеет вид:

где
 -
многочлен степени m.
-
многочлен степени m.
Тогда частное решение ищется в виде:

Здесь Q(x)- многочлен той же степени, что и P(x), но с неопределенными коэффициентами, а r – число, показывающее сколько раз число является корнем характеристического уравнения для соответствующего линейного однородного дифференциального уравнения.
Пример.
Решить уравнение
 .
.
Решим
соответствующее однородное уравнение:



Теперь найдем частное решение исходного неоднородного уравнения.
Сопоставим правую часть уравнения с видом правой части, рассмотренным выше.

Частное
решение ищем в виде:
,
где
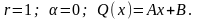
Т.е.

Теперь определим неизвестные коэффициенты А и В.
Подставим частное решение в общем виде в исходное неоднородное дифференциальное уравнение.


Итого,
частное решение:

Тогда общее решение линейного неоднородного дифференциального уравнения:

 II.
Правая часть линейного неоднородного
дифференциального уравнения имеет вид:
II.
Правая часть линейного неоднородного
дифференциального уравнения имеет вид:

Здесь Р1(х) и Р2(х) – многочлены степени m1 и m2 соответственно.
Тогда частное решение неоднородного уравнения будет иметь вид:

где
число r
показывает сколько раз число
 является корнем характеристического
уравнения для соответствующего
однородного уравнения, а Q1(x)
и
Q2(x)
– многочлены степени не выше m,
где m-
большая из степеней m1
и m2.
является корнем характеристического
уравнения для соответствующего
однородного уравнения, а Q1(x)
и
Q2(x)
– многочлены степени не выше m,
где m-
большая из степеней m1
и m2.
Заметим, что если правая часть уравнения является комбинацией выражений рассмотренного выше вида, то решение находится как комбинация решений вспомогательных уравнений, каждое из которых имеет правую часть, соответствующую выражению, входящему в комбинацию.
Т.е.
если уравнение имеет вид:
 ,
то частное решение этого уравнения
будет
,
то частное решение этого уравнения
будет
 где
у1
и у2
– частные решения вспомогательных
уравнений
где
у1
и у2
– частные решения вспомогательных
уравнений
 и
и

Для иллюстрации решим рассмотренный выше пример другим способом.
Пример.
Решить уравнение
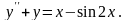
Правую часть дифференциального уравнения представим в виде суммы двух функций f1(x) + f2(x) = x + (-sinx).
Составим
и решим характеристическое уравнение:

Для
функции f1(x)
решение ищем в виде
 .
.
Получаем:
 Т.е.
Т.е.


Итого:

Для
функции f2(x)
решение ищем в виде:
 .
.
Анализируя
функцию f2(x),
получаем:

Таким
образом,




Итого:

Т.е.
искомое частное решение имеет вид:

Общее решение неоднородного дифференциального уравнения:

Вопрос 39. Комплексные числа.
z= x+yi – алгебраическая форма записи комплексного числа, где x – действительная часть к.ч., y – мнимая часть к.ч.
i – мнимая единица
i2=
-1 ; i=

|z|=
 – расстояние от 0 до z
– расстояние от 0 до z
z с чёрточкой = x-iy (сопряжённое данному к.ч.)
Если z=0 => x и y тоже =0
Операции с к.ч.
+,-,*,/
Как в алгебре (не забывать, что i*i= -1)
Аргумент к.ч. определён не однозначно, а с точностью 2πk, k пр. Z
Argz=argфи+2πk, k пр.Z
x=2cosфи
y=2sinфи
z=x+iy
z=r(cosфи+isinфи)
r|z|=
Деление/умножение к.ч.
z1=r1(cosфи1+isinфи1)
z2=r2(cosфи2+isinфи2)
z1*z2= r1r2(cosфи1+isinфи1)(cosфи2+isinфи2)=
= r1r2(cos(фи1+фи2)+isin(фи1+фи2))
 =
=
 (cos(фи1-фи2)+isin(фи1-фи2))
(cos(фи1-фи2)+isin(фи1-фи2))
zn= rn(cosnфи+isinnфи)
Формула для корня к.ч.
w=
 ó
wn=z
ó
wn=z
z= r(cos(фи+2πk)+isin(фи+2πk))
w= ρ(cosпси+isinпси)
ρn(cosnпси+isinnпси)=
=r(cos(фи+2πk)+isin(фи+2πk))
ρn
=
r ó
ρ =
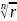
nпси=фи+2πk ó пси= (фи+2πk)/n
псиn=(фи+2π(n-1)/n
wn=
(cos
 +isin
)
+isin
)
Показательная форма. Формула Эйлера.
eiфи= cosфи+isinфи
cosфи= (eiфи+ e-iфи)/2
sinфи= (eiфи- e-iфи)/2
z= x+yi
ez=ex+yi=ex * eiy = ex(cosфи+isinфи)
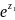 *
* =
=
 *
* =
=
=
 (cosy1+isiny1)*
(cosy1+isiny1)* (cosy2+isiny2)=
(cosy2+isiny2)=
=
 *
*
 =
=
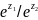 =
=
 =
ez
*
e2πi=ez(cos2π+isin2π)=ez
=
ez
*
e2πi=ez(cos2π+isin2π)=ez
т.о., ez является периодичной функцией с периодом 2πi
