Вопрос 27. Теорема о замене переменной в определенном интеграле.

Пусть интегрируема и непрерывна на , непрерывна и дифференцируема на , причем и , тогда

Док-во. Пусть некоторая первообразная для ,

тогда — первообразная для функции .

Действительно,

По формуле Ньютона-Лейбница, левая часть = , правая часть = , т.к. и , то левая часть равна правой части.

Интегрирование по частям в определенном интеграле.

Док-во. Функция является первообразной для функции , действительно,

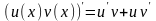
Следовательно — формула Ньютона-Лейбница, или

Замена переменной в неопределённом интеграле (интегрирование подстановкой).

Пусть . Тогда . Здесь t(x) - дифференцируемая монотонная функция.

Док-во непосредственно следует из формулы для производной сложной функции. Перепишем первый интеграл, заменив переменную x на t: . Это означает, что . Заменим независимую переменную t на функцию t = t(x): . Следовательно, функция F(t(x)) является первообразной для произведения , или .

При решении задач замену переменной можно выполнить двумя способами.

1. Если в подынтегральной функции удаётся сразу заметить оба сомножителя, и f(t(x)), и , то замена переменной осуществляется подведением множителя под знак дифференциала: , и задача сводится к вычислению интеграла . Например, (задача сведена к вычислению , где t = cos x) (аналогично находится интеграл от ); (задача сведена к вычислению , где t = sin x) .

2. Замену переменной можно осуществлять формальным сведением подынтегрального выражения к новой переменной. Так, в имеет смысл перейти к переменной (сделать подстановку) t = sin x. Выражаем все множители подынтегрального выражения через переменную t: ; в результате (возвращаемся к исходной переменной) .

ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ.

Интегрирование по частям - приём, который применяется почти так же часто, как и замена переменной. Пусть u(x) и v(x) - функции, имеющие непрерывные частные производные. Тогда по формуле дифференцирования произведения d(uv) = u∙dv + v∙du . Находим неопределённые интегралы для обеих частей этого равенства (при этом ): . Эта формула и называется формулой интегрирования по частям. Часто ее записывают в производных ( ): . Примеры: .

.

Формула интегрирования по частям может применяться неоднократно. При наличии небольшого опыта в простых интегралах нет необходимости выписывать промежуточные выкладки (u = …, dv = …), можно сразу применять формулу, представив интеграл в виде :

.

Вопрос 28. Несобственные интегралы.

(несобственные интегралы первого рода). Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла при называется несобственным интегралом функции f(x) от a до и обозначается . Итак, по определению, . Если этот предел существует и конечен, интеграл называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.

Аналогично интегралу с бесконечным верхним пределом интегрирования определяется интеграл в пределах от до b : и в пределах от до : . В последнем случае f(x) определена на всей числовой оси, интегрируема по любому отрезку; c - произвольная (собственная) точка числовой оси; интеграл называется сходящимся, если существуют и конечны оба входящих в определение предела. Существование конечных пределов и их сумма не зависят от выбора точки c. Очевидно следующее утверждение, которое мы сформулируем для интеграла с бесконечным верхним пределом: сходится тогда и только тогда, когда для любого c, удовлетворяющего неравенству c > a, сходится интеграл (док-во: так как при a < c < b по свойству аддитивност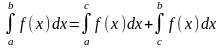и , и от b не зависит, то конечный предел при для интеграла в левой части существует тогда и только тогда, когда существует конечный предел для интеграла в правой части равенства)

(несобственные интегралы второго рода). Определение несобственного интеграла от неограниченной функции. Особенность на левом конце промежутка интегрирования. Пусть функция f(x) определена на полуинтервале (a, b], интегрируема по любому отрезку , и имеет бесконечный предел при . Несобственным интегралом от f(x) по отрезку называется предел . Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится. Особенность на правом конце промежутка интегрирования. Пусть функция f(x) определена на полуинтервале [a, b), интегрируема по любому отрезку , и имеет бесконечный предел при . Несобственным интегралом от f(x) по отрезку [a, b] называется предел . Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится. Особенность во внутренней точке промежутка интегрирования. Пусть функция f(x) определена на отрезке [a, b], имеет бесконечный предел при стремлении аргумента к какой-либо внутренней точке c этого отрезка: , интегрируема по любому отрезку, не содержащему точку c. Несобственным интегралом от f(x) по отрезку [a, b] называется . Интеграл сходится, если оба эти пределы существуют и конечны, в противном случае интеграл расходится.