1.4 Характеристики чувствительности си к влияющим величинам

1.4.1 Функция влияния .

1.4.2 Изменения значений МХ СИ, вызванные изменениями влияющих величинв установленных пределах.

1.5 Динамические характеристики си

1.5.1 Полная динамическая характеристика аналоговых СИ, которые можно рассматривать как линейны, выбирается из числа следующих:

- переходная характеристика ;

- импульсная переходная характеристика ;

- амплитудно-фазовая характеристика ;

- амплитудно-частотная характеристика - для минимально-фазовых СИ;

- совокупность амплитудно-частотной и фазово-частотнойхарактеристик;

- передаточная функция .

1.5.2 Частные динамические характеристики аналоговых СИ, которые можно рассматривать как линейные. К частным динамическим характеристикам относят любые функционалы или параметры полных динамических характеристик, например:

- время реакции ;

- коэффициент демпфирования ;

- постоянная времени ;

- значение амплитудно-частотной характеристики на резонансной

частоте ;

- значение резонансной собственной круговой частоты .

1.5.3 Частные динамические характеристики АЦП и ЦИП, время реакции которых не превышает интервала времени между двумя измерениями, соответствующего максимальной частоте (скорости) измерений, а также ЦАП. Примерами частных динамических характеристик АЦП являются:

- время реакции ( в том числе для ЦАП);

- погрешность датирования отсчета;

- максимальная частота (скорость) измерений .

1.5.4 Динамические характеристики аналого-цифровых СИ (в том числе измерительных каналов измерительных систем и измерительно-вычислительных комплексов, оканчивающихся АЦП), время реакции которых больше интервала времени между двумя измерениями, соответствующего максимально возможной для данного типа СИ частоте (скорости) измерений:

- полные динамические характеристики эквивалентной аналоговой части аналого-цифровых СИ;

- погрешность датирования отсчета ;

- максимальная частота (скорость) измерений .

Из числа представленных групп МХ СИ подробно рассмотрим нормирование динамических характеристик СИ, поскольку другие МХ рассматриваются в соответствующих разделах метрологии.

В ГОСТ 8.009 предусмотрено нормирование таких динамических характеристик СИ, которые позволяют оценивать искажения средствами измерения любых изменяющихся сигналов, поступающих на их вход – исследуемых при измерениях (динамическая составляющая погрешности измерений), и сигналов, эквивалентных статической погрешности СИ, поступающих в данное СИ в измерительной системе (статическая погрешность измерительной системы),

Для линейных СИ такими характеристиками являются так называемые полные динамические характеристики, представляющие собой функции, связывающие между собой изменяющиеся во времени входной сигнал и вызываемый им выходной сигнал СИ. По ГОСТ 8.009 полная динамическая характеристика СИ определяется как динамическая характеристика, полностью описывающая принятую математическую модель динамических свойств СИ. Причем описание может быть математическим, графическим, в виде таблицы и т. п.

Эти характеристики для линейных звеньев между собой связаны однозначно, поэтому в каждом конкретном случае следует нормировать ту из них, которой в данном случае удобнее пользоваться и которую удобнее экспериментально оценивать (контролировать).

Полные динамические характеристики линейных аналоговых СИ однозначно связаны между собой следующими соотношениями:

- переходная характеристика

- импульсная переходная характеристика

- амплитудно-фазовая характеристика

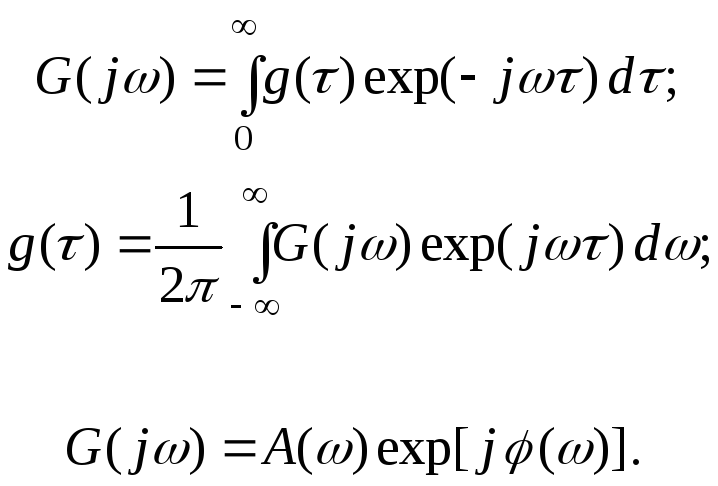
- передаточная функция

В теории автоматического управления кроме указанных характеристик используют вещественную частотную характеристику и мнимую частотную характеристику, которые связаны с полными динамическими характеристиками следующими соотношениями:

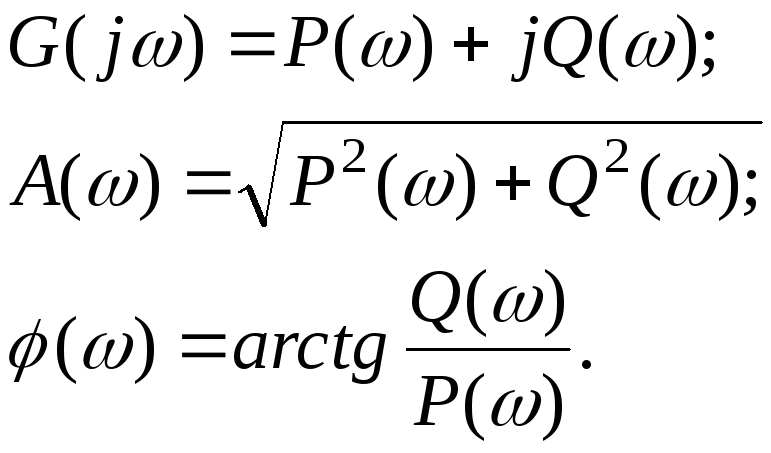
Если СИ обладает амплитудно-фазовой характеристикой минимально-фазового типа, то его фазово-частотная характеристика однозначно связана с логарифмической амплитудно-частотной характеристикой

,

где ;

- переменная интегрирования, имеющая размерность круговой

частоты.

Если динамические свойства СИ описываются дифференциальным уравнением

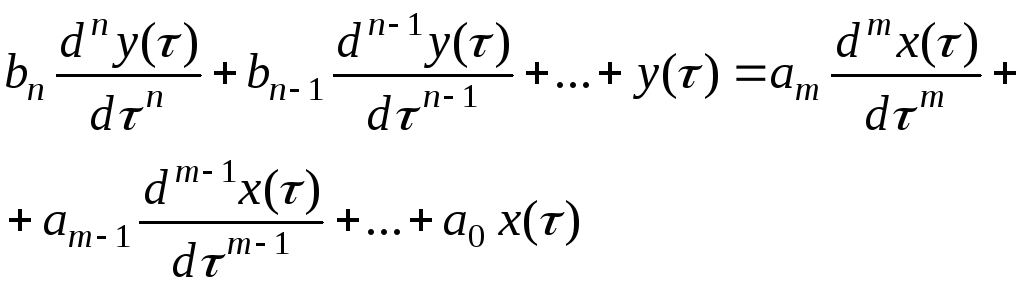
с нулевыми начальными условиями, то передаточная функция и амплитудно-фазовая характеристики имеют дробно-рациональное представление с коэффициентами из дифференциального уравнения:

(1.1)

Для оценки инструментальной составляющей погрешности измерений наиболее удобна амплитудно-фазовая характеристика, однако, она не всегда может быть экспериментально определена с помощью прямых методов измерений.

С точки зрения экспериментального определения наиболее удобными динамическими характеристиками являются переходная и амплитудно-частотная характеристики. Действительно, при подаче на вход СИ испытательного ступенчатого сигнала единичного размера можно с помощью прямых измерений выходного сигнала получить отсчеты (или запись) переходной характеристики. Амплитудно-частотная характеристика также может быть получена с помощью прямых измерений амплитуды выходных гармонических сигналов при действии на входе гармонических сигналов требуемой частоты и единичной амплитуды.

Однако здесь возникает трудность, связанная с ограниченными возможностями точного воспроизведения формы сигналов тех или измеряемых величин. Например, трудно воспроизвести гармоническое изменение температуры, концентрации сложных веществ, влажности, расхода. С другой стороны, скачкообразное изменение таких величин, как, например, скорости и ускорения воспроизвести труднее, чем гармоническое.

Все перечисленные обстоятельства следует учитывать при выборе той или иной динамической характеристики для нормирования. Нормировать рекомендуется такую характеристику, которая может быть экспериментально определена с помощью наиболее простых методов измерений.

Для моделирования динамической составляющей погрешности измерений наиболее удобны импульсная переходная и амплитудно-фазовая характеристики, а также передаточная функция.

Импульсная переходная характеристика используется при цифровом моделировании путем приближенного вычисления выходного сигнала СИ

.

Амплитудно-фазовая характеристика и передаточная функция часто используются для моделирования СИ на вычислительных машинах.

Для расчета МХ измерительных каналов измерительных систем, состоящих из СИ, наиболее приемлемы передаточная функция и амплитудно-фазовая характеристика. При этом для определения, например, передаточной функции всей измерительной системы, состоящей из последовательных, параллельных или комбинированно соединенных СИ, используют правила, применяемые в теории автоматического управления.

Что касается импульсной переходной характеристики измерительной системы, то для последовательного соединения она, как известно, равна свертке импульсных переходных характеристик отдельных звеньев, а при параллельном соединении – сумме импульсных характеристик.

Возможность применения динамических характеристик для оценки динамической погрешности СИ можно продемонстрировать на примере передаточной функции.

Предположим, что передаточная функция СИ нормирована в виде (1.1). При этом должны быть известными значения и.

Нормированию подлежат номинальные значения икоэффициентовии их наибольшие допускаемые отклоненияиот номинальных значений. Величиныииспользуют только для контроля качества СИ при испытаниях. При расчетах динамической составляющей погрешности применяют величиныи.

Если на вход СИ подается сигнал , то выходной сигнал в операторной форме выражается

Номинальная статическая функция преобразования СИ может быть принята в виде

Тогда динамическая погрешность СИ по выходы в операторной форме выражается формулой

где

.

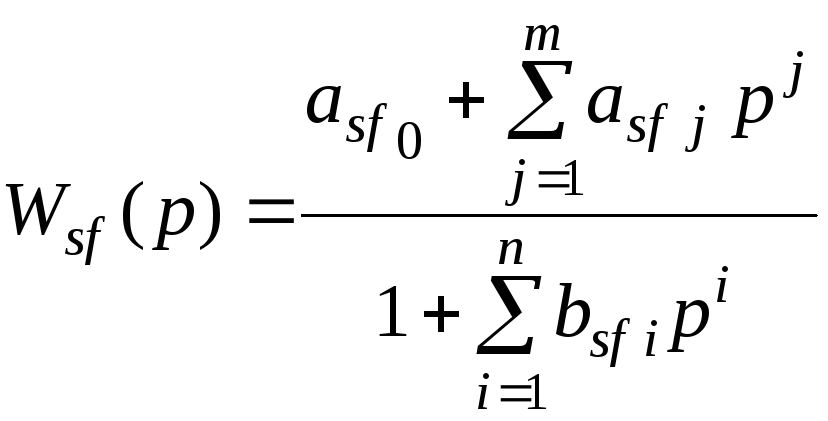Динамическая погрешность СИ по входу выражается формулой

.

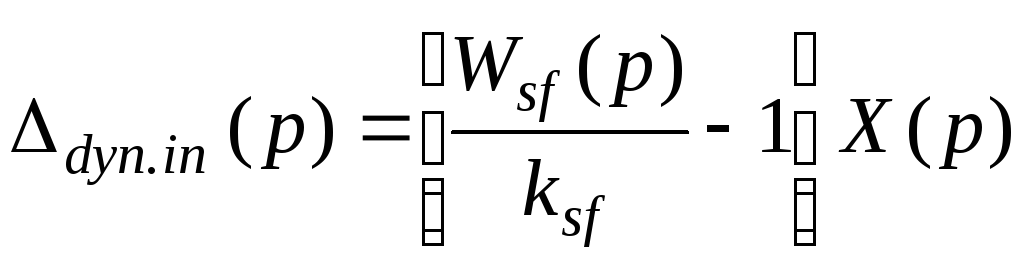Из передаточной функции можно также получить переходную характеристику СИ с помощью обратного преобразования Лапласа:

. (1.2)

Импульсная переходная характеристика СИ связана, в свою очередь, с переходной характеристикой следующим соотношением

.

Таким образом, по передаточной функции могут быть найдены все характеристики, отражающие динамические свойства СИ в действующей НТД.

В отличие от полных динамических характеристик, по частным динамическим характеристикам нельзя вычислить динамическую составляющую погрешности измерений. В соответствии с ГОСТ 8.009 частная динамическая характеристика СИ определяется как функционал или параметр полной динамической характеристики СИ. Используя частные динамические характеристики, можно ориентировочно сопоставить свойства СИ в условиях измерения. В некоторых случаях вполне допустимо нормировать только частные динамические характеристики. Например, для стрелочных приборов, предназначенных для измерений постоянных или медленно меняющихся величин, указания в НТД времени реакции достаточно для того, чтобы оператору определить время считывания показаний измерительного прибора. Другим примером могут являться магнитоэлектрические осциллографические гальванометры, для которых в НТД нормируются только частные динамические характеристики - частота собственных колебаний (частота, при которой возможен резонанс)и степень успокоения.

В теории автоматического регулирования динамические характеристики звеньев подразделяются на временные и частотные.

К временным характеристикам звеньев относятся переходная и импульсная переходная характеристики, а к частотным – амплитудно-фазовая частотная характеристика (АФЧХ), амплитудно-частотная характеристика, фазово-частотная характеристика, вещественная частотная и мнимая частотная характеристики. Таким образом, в теории автоматического регулирования применяются пять частотных характеристик в отличие от ГОСТ 8.009, по которому можно нормировать три частотные характеристики СИ. Кроме того, по ГОСТ 8.009 рекомендуется использовать термин не АФЧХ, а АФХ – амплитудно-фазовая характеристика СИ.

Частотные характеристики СИ широко используются в инженерной практике, особенно построенные в логарифмическом масштабе. В настоящее время метод логарифмических частотных характеристик является одним из основных методов анализа и синтеза измерительных систем. Это связано с тем, что при переходе к логарифмам операции умножения значений величин заменяются более простыми операциями сложения их логарифмов и, кроме того, крутизна зависимостей в логарифмическом масштабе существенно уменьшается. Это дает возможность аппроксимировать частотные характеристики, построенные в логарифмическом масштабе, в виде ломаных линий из прямоугольных отрезков.

Логарифмируя амплитудно-фазовую характеристику, получаем:

Логарифмической единицей усиления или ослабления мощности сигнала при прохождении его через какое-либо устройство, в том числе через СИ, при выражении десятичным логарифмом значения отношения мощности на выходе к мощности на входев технике принятбел ().

По определению амплитудно-частотной характеристикой СИ является зависящее от круговой частоты отношение амплитуды выходного сигнала линейного СИ в установившемся режиме к амплитуде входного синусоидального сигнала, т. е.

.

Так как мощность сигнала пропорциональна квадрату его амплитуды, то для логарифма отношений мощностей получим:

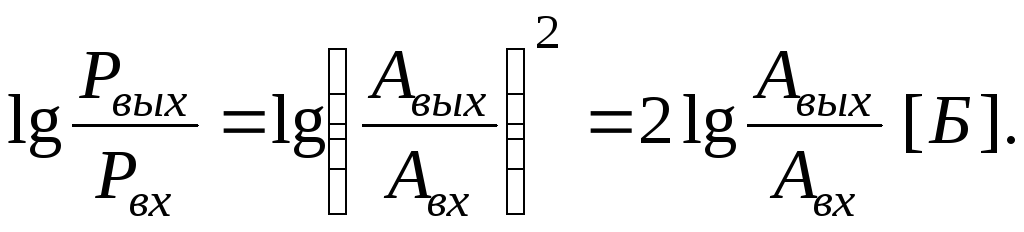
Так как бел является достаточно крупной единицей усиления (ослабления) мощности (увеличение мощности в 10 раз равно одному белу), то за единицу измерения принят децибел ().

С учетом этого можно записать:

Эта величина, обозначаемая

называется логарифмической амплитудно-частотной характеристикой СИ.

Фазово-частотная характеристика , построенная в полулогарифмическом масштабе (в координатах угол-называется логарифмической фазово-частотной характеристикой СИ.

За единицу измерения частоты принимается логарифмическая единица октава или более крупная – декада.

Октавой называется диапазон частот между какой-либо частотой и ее удвоенным значением. В логарифмическом масштабе частот отрезок в одну октаву имеет одну и ту же длину, не зависящую от и равную:

Декадой называется интервал частот между какой-либо частотой и ее десятичным значением. В логарифмическом масштабе частот отрезок в одну декаду, так же как и в одну октаву, не зависит от частоты и имеет длину, равную: