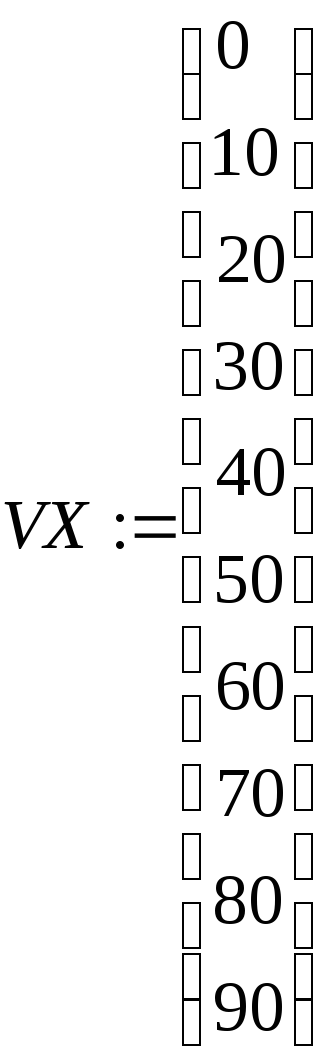4.3.2 Выбор функции регрессии

В качестве функции регрессии следует выбирать ту функцию, которой соответствует экспериментальная характеристика ИСИ.

Для экспериментальной переходной характеристики ИСИ это переходная функция .

Для экспериментальной импульсной переходной характеристики ИСИ это импульсная переходная функция .

Для экспериментальной амплитудно-частотной характеристики это амплитудно-частотная функция и т. д.

На практике при определении динамических характеристик СИ чаще всего в качестве функции регрессии выбирают переходную функцию и ищут ее параметры для соответствующих динамических моделей.

4.3.3 Системы дифференциальных уравнений для различных динамических моделей си

Ниже приведены системы дифференциальных уравнений в частных производных, выведенных для типовых динамических моделей (см. таблицу 1.1) с учетом вида их переходных функций (см. приложение А). Частные производные от отклонения по параметрам переходных функций выведены с использованием шаблона дифференцирования в системеMathcad 2000.

Обозначение соответствуетв выражении (4.3).

а) ДМ № 3. Апериодическое 1-го порядка СИ:

б) ДМ № 4. Апериодическое 1-го порядка СИ с форсированием:

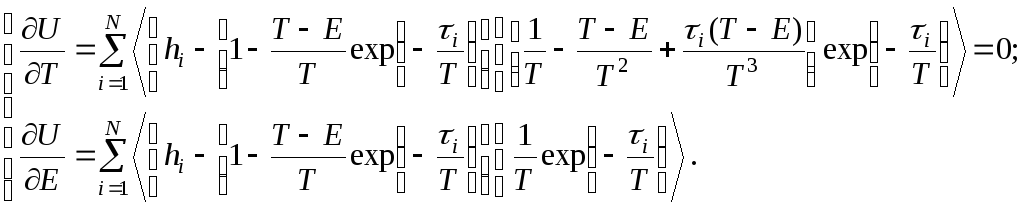
в) ДМ № 5. Апериодическое 2-го порядка СИ:

г) ДМ № 6. Апериодическое 2-го порядка СИ с форсированием:

д) ДМ № 7. Колебательное СИ:

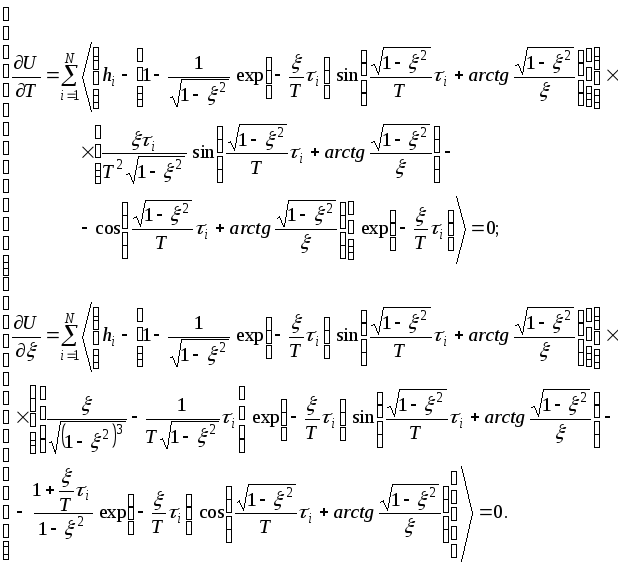
е) ДМ № 8. Двукратное апериодическое СИ:

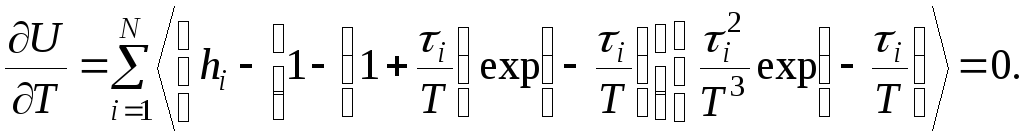
ж) ДМ № 9. Апериодическое 1-го порядка с транспортным запаздыванием.

Определение постоянной времени производится по уравнению для ДМ № 3. Транспортное запаздываниеопределяется непосредственно из экспериментальной переходной характеристики ИСИ.

и) ДМ № 11. Интегрирующее СИ с замедлением 2-го порядка:

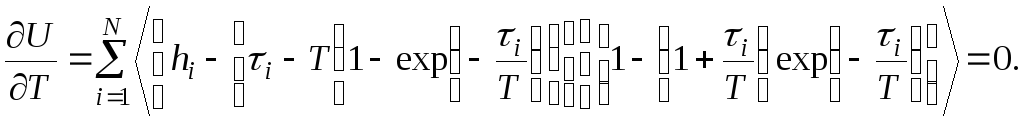
к) ДМ № 14. Дифференцирующее СИ с замедлением 1-го порядка:

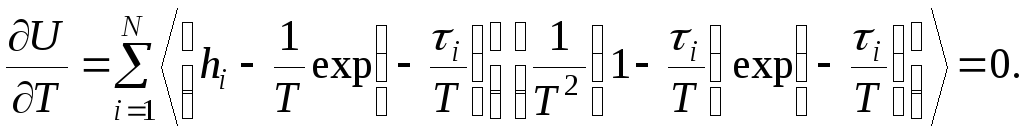
л) ДМ № 15. Дифференцирующее СИ с замедлением 2-го порядка:

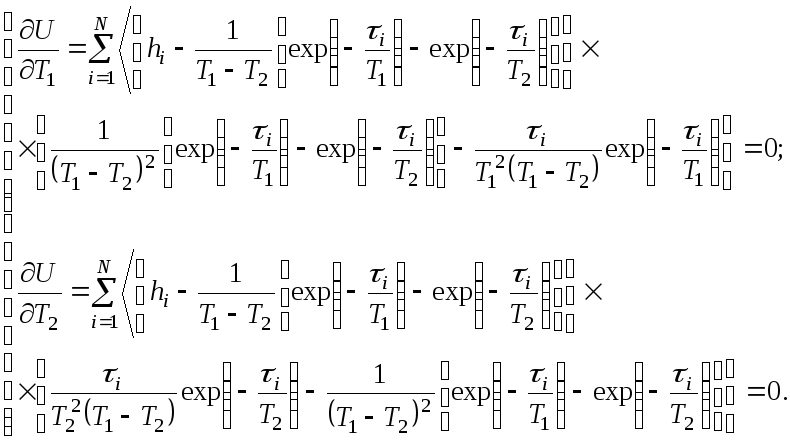
Для ДМ № 1, ДМ № 2, ДМ № 10, ДМ № 12 и ДМ №13 дифференциальные уравнения не приведены, так как часть моделей относится к идеальным (т.е. не существующим на практике) СИ, а другая часть легко описывается линейной функцией регрессии.

4.3. 4 Реализация регрессионного анализа

Как видно из приведенных систем дифференциальных уравнений в частных производных, они являются достаточно сложными по виду. Поэтому на практике их решают с использованием стандартных программ, имеющихся в различных системах автоматизации математических вычислений.

Рассмотрим проведение нелинейной регрессии общего в системе Mathcad 2000 на примере поиска параметров переходной функции ДМ № 3. В качестве исходных данных используем выходной сигнал ИСИ, изображенный на рисунке 4.3, и таблицу его отсчетов (см. таблицу 4.4). Так как истинное значение постоянной времени рассматриваемой ДМ № 3 известно (), то впоследствии можно будет оценить точность проведения регрессионного анализа. Кроме того, из таблицы 4.4 выберем не все, а только 10 значений зарегистрированной переходной характеристики, т. е..

Для проведения нелинейной регрессии общего вида используется функция , которая возвращает векторпараметров функции, дающий минимальную среднеквадратичную погрешность приближения функциейисходных данных.

Вектор должен быть вектором с символьными элементами, причем они должны содержать аналитические выражения для исходной функции и ее производных по всем параметрам. Вектордолжен содержать начальные значения элементов вектора, необходимые для решения системы нелинейных уравнений регрессии итерационным методом.

В таблице 4.6 приведена реализация данной нелинейной регрессии в системе Mathcad 2000.

Как видно из таблицы 4.5 результат вычисления постоянной времени дает значение , что отличается от истинного значения на. Это вполне достаточная точность определения постоянной времени ИСИ, имеющего динамическая модель № 3, по экспериментальной переходной характеристике с таким уровнем случайного сигнала (помехи).

Таблица 4.6 – Реализация нелинейной регрессии в системе Mathcad 2000

Нелинейная регрессия

Комментарии

Исходная функция регрессии: Производная исходной функции по параметру . Системная переменная. Начало массива. Определяет индекс первого элемента массива. Вектор с символьными элементами исходной функции и ее производной по параметру Вектор значений времени переходной характеристики в . Вектор значений переходной характеристики в. Вектор содержащий начальное (приближенное) значение искомой постоянной времени в . Функция, возвращающая вектор параметров функции , который дает минимальную среднеквадратичную погрешность приближения. Результат решения: .