5 Определение переходных функций средств измерений по передаточным функциям

Математической основой классификации линейных аналоговых СИ является передаточная функция вида [4, с. 92]:

. (5.1)

Как известно, знание передаточной функции позволяет с учетом обратного преобразования Лапласа найти переходную функцию по выражению

, (5.2)

где .

Обратный переход от изображения к оригиналу обычно связан с громоздкими вычислениями в области комплексных чисел. Поэтому в теории автоматического управления нашли применение математические формулы, охватывающие широкий класс практических задач, которые успешно могут быть применены для определения переходных функций СИ.

Случай 1. Предположим, что в (5.1) ,,и. Тогда

, (5.3)

где - корни уравнения.

Формулу (5.3) иногда называют второй теоремой разложения Хевисайда.

Пример. Пусть СИ описывается передаточной функцией вида

.

Корнями уравнения являются

,

а производная функции поравна:

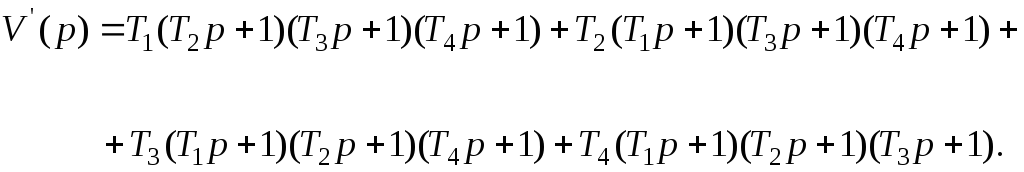
После подстановки в (5.3) полученных выражений переходная функция принимает вид

,

где

Случай 2. Предположим, что в (5.1) ,,и, а все корни уравнениякратные, т. е.

,

где - число кратных корней.

Тогда переходная функция СИ определяется выражением вида

. (5.4)

Пример. Пусть СИ описывается передаточной функцией вида (=2)

.

Тогда переходная функция данного СИ с учетом (6) примет вид

.

Для некоторых других видов передаточных функций средств измерений, которые описываются выражением (5.1), в [2, с. 48] приведены соответствующие уравнения переходных функций.

6 Фильтрация сигналов измерительной информации

6.1 Сигналы измерительной информации

Сигналом измерительной информации называется сигнал, функционально связанный с измеряемой физической величиной.

Сигнал измерительной информации имеет информативный параметр – параметр, функционально связанный с измеряемой величиной. Параметры сигнала, не связанные функционально с измеряемой величиной, называют неинформативными параметрами.

Как видно из рисунка 3.1 сигналом измерительной информации с ИСИ, несущим информацию о его динамических свойствах, является сигнал . При проведении эксперимента редко удается зарегистрировать с помощью регистрирующего прибора непосредственно сам сигнал. Чаще всего требуется его преобразовать в другой вид для последующей передачи, хранения, обработки или восприятия регистрирующим прибором. В измерительной системе (установке) эту функцию могут выполнять измерительные преобразователи. Следует иметь в виду, что измерительные преобразователи как полноправные СИ, имеют свои нормированные метрологические характеристики, которые также нужно учитывать при проведения эксперимента.

В случае наличия в сигнале случайного сигнала (помехи)с высоким уровнем необходимо в измерительную систему включать устройства подавления помех, которые называются фильтрами сигналов.

Фильтры могут быть встроены в измерительные преобразователи или же быть самостоятельными функциональными элементами измерительной системы.

На рисунке 6.1 представлен пример реализации измерительной системы с измерительным преобразователем и фильтром.

ГИС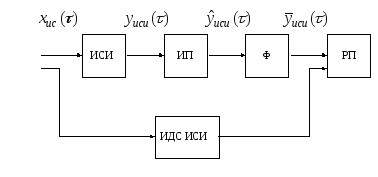

ГИС – генератор испытательного сигнала;

ИСИ – исследуемое СИ; ИП – измерительный преобразователь;

Ф – фильтр; РП – регистрирующий прибор;

ИДС ИСИ – имитатор динамического свойства ИСИ

Рисунок 6.1 – Структурная схема измерительной системы

Здесь - сигнал с выхода измерительного преобразователя, сохранивший информацию о динамических свойствах ИСИ. Сигнал- это сигнал с выхода фильтра, в котором сохранена информация о динамических свойствах ИСИ и существенна уменьшена помеха.

В подавляющем числе случаев сигнал является электрическим, поэтому рассмотрим применение электрических фильтров в измерительной системе, изображенной на рисунке 6.1.