19. Теория игр. Оптимальность стратегий .

Теория игр . Основные результаты теории игр впервые получены в военной области.

Основные работы теории игр - Дж. фон Нейман и Оскар Моргенштерн (теория игр и экономическое поведение)

Рассмотрим игру двух лиц с конечным числом чистых стратегий.

2 игрока поочередно разыгрывают партии: в каждой партии один игрок выбирает ходы из множества

Sm 1, 2…m

S n 1, 2…n

В каждой партии I,j ходов. Выигрыш 1 ого игрока аij , 2ого игрока – аij.

Игра с нулевой суммой

М атрица выигрышей:

А= а11, а12….а1n - для всех комбинаций ходов

а21, а22…..а2n

……………………..

am1, am2….amn

Игроки выбирают ходы с различными вероятностями

Р=(Р1, Р2…Рm) Pi- вероятности выбора ходов 1ого игрока. Стратегии 1ого игрока

Q=(Q1, Q2…Qm) Qi - вероятности выбора ходов 2ого игрока. Стратегии 2ого игрока

Математическое ожидание выигрыша = функция выигрыша –величина

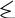m n

E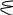 (P,Q) = aij pi qj

I=1 j=1

Оптимальность стратегии

P*, Q* - оптимальность стратегии

V – цена игры если выполняется неравенство

E( P,Q*)<= V<= E(P*,Q)

V=E(P*,Q*)

P,Q – любые стратегии

Основное неравенство теории игр показывает, что если второй игрок будет применять свою стратегию, то при любых стратегиях первого его выигрыш будет не более, чем цель игры. И наоборот.

Билет 20

Теорема Дж.фон Неймана (Лемма 1)

Основная теорема Неймана: любая матричная игра имеет решение. Для доказательства этой теоремы используют две леммы (вспомогательные теоремы).

Лемма 1: Если к матрице выигрышей прибавить какое-либо число, то оптимальная стратегии не изменятся, а цена игры изменится на это число.

Док-во: Рассмотрим игру «Гамма»

Г: Е_г(P,Q^*)≤V≤ Е_г(P^*,Q)

Е_г(P,Q)=

A+α;

Е_г^’(P,Q)= = Е_г(P,Q)+α

Билет 21

Теорема Дж.фон Неймана (Лемма 2)

Основная теорема Неймана: любая матричная игра имеет решение. Для доказательства этой теоремы используют две леммы (вспомогательные теоремы).

Лемма 2: матричная игра с положительной матрицей имеет решение.

Рассмотрим матричную игру с матрицей 2*3

А=

Составим исходную и двойственную задачу ЛП по способу Данцига

min f(x̅)=x1+x2 a11x1+a21x2≥1 a12x1+a22x2≥1 a13x1+a23x2≥1 x1≥0 x2≥0 x2≥0

max g(y̅)=y1+y2+y3 y1≥0 y2≥0 y3≥0 a11y1+a12y2 +a13y3≤1 a21y1+a22y2 +a23y3≤1

Положим, что каждая из этих задач имеет решение, следовательно, они будут иметь и оптимальное решение.

Двойственная задача имеет план y̅(0;0);

Покажем, что исходная задача также имеет план или допустимое решение.

x̅(0;0) не является планом задачи. Будем искать допустимое решение в виде x̅(x₁;0)

a₁₁x₁≥1; a₁₂x₁≥1; a₁₃x₁≥1;

x₁≥1/ a₁₁; x₁≥1/ a₁₂; x₁≥1/ a₁₃;

x₁≥max(1/ a₁₁; 1/ a₁₂;1/ a₁₃₎

x̅(x₁;0) – решение задачи.

Исходная и двойственная задача имеют планы, а значит они имеют и оптимальные планы. По 1-ому критерию оптимальности пары двойственных задач, функции цели на оптимальных планах исходной и двойственной задач равны.

f(x̅^*)=x₁^*+ x₂^*= y₁^*+ y₂^*+ y₃^*=g(y̅^*)=μ

Покажем, что из данных планов можно получить стратегии.

P( Q( P, Q – стратегии игроков.

0≤ ≤1; 0≤ ≤1;

+ =1

Аналогично для компонент вектора Q.

Покажем, что эти стратегии являются оптимальными, т.е. для них выполняется основное неравенство теории игр.

a₁₁x₁^*+a₂₁x₂^*≥1 *q₁/μ

+ a₁₂x₁^*+a₂₂x₂^*≥1 *q₂/μ

a₁₃x₁^*+a₂₃x₂^*≥1 *q₃/μ

a₁₁ q₁+ a₂₁ q₁+ a₁₂ q₂+ a₂₂ q₂+ a₁₃ q₃+ a₂₃ q₃=

a₁₁p₁^*q₁+ a₂₁p₂^*q₁+ a₁₂p₁^*q₂+ a₂₂p₂^*q₂+ a₁₃p₁^*q₃+ a₂₃p₂^*q₃ ≥

E(P^*,Q) ≥

Аналогично для двойственной задачи:

a₁₁y₁^*+a₁₂y₂ ^*+a₁₃y₃^*≤1 * p₁/μ

+ a₂₁y₁^*+a₂₂y₂ ^*+a₂₃y₃^*≤1 * p₂/μ

E(P,Q^*) ≤

E(P,Q^*) ≤ ≤ E(P^*,Q)

E(P^*,Q^*)=

P^*,Q^* - оптим.стратегии, V – цена игры, => Теорема доказана