Теория двойственности

 

Составление двойственных задач

Каждой задаче линейного программирования можно поставить в соответствие другую задачу линейного программирования, которую называют двойственной к данной. Исходная и двойственная к ней задача образуют пару двойственных задач.

В зависимости от вида исходной задачи линейного программирования различают симметричные, несимметричные и смешанные пары двойственных задач.

Симметричные пары двойственных задач

Определение 1. Если система ограничений исходной задачи состоит из неравенств и на все переменные х_j наложено условие неотрицательности, то исходная задача и составленная по определенному правилу двойственная задача образуют симметричную пару двойственных задач.

Пусть исходная задача имеет вид: найти наибольшее значение функции

при ограничениях:

                                                                      

  .

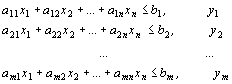
Правило составления двойственных задач

1.    Каждому ограничению исходной задачи ставится в соответствие двойственная переменная y_i, где  .

2.    Составляется целевая функция  , коэффициентами которой будут свободные члены системы ограничений исходной задачи, а цель задачи меняется на противоположную:

.                             (1)

3.    Составляется система ограничений двойственной задачи, при этом матрица из коэффициентов системы ограничений исходной задачи транспонируется, знак неравенства меняется на противоположный, свободными членами будут являться коэффициенты из целевой функции исходной задачи:

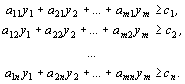       Основное неравенство двойственности

Для любых допустимых решений прямой задачи х и для любых допустимых решений двойственной задачи у выполняется неравенство   

Доказательство.

Из системы ограничений задачи    

Из системы ограничений задачи 

Объединяя полученные неравенства, имеем  

Теорема доказана.

8. Основная теорема двойственности. Достаточные признаки оптимальности планов пары двойственных задач.

Основная Теорема. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны. Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.

Или другая формулировка: “Теорема двойственности”. Если обе задачи имеют допустимые решения, то они имеют и оптимальные решения, причем значение целевых функций у них будет одинаково:

Экономическое содержание первой теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки, обладают тем свойством, что они гарантируют рентабельность оптимального плана, т. е. равенство общей оценки продукции и ресурсов, и обусловливают убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставить и сбалансировать затраты и результаты системы.

Достаточный признак оптимальности.

Если X*=(x*1, x*2,…, x*n) и У*=(у*1, у*2,…, у*n) – допустимые решения взаимно двойственных задач, для которых выполняется равенство

F(X*) =Z(Y*)

то Х* оптимальное решение исходной задачи I, а У* - двойственной задачи II.

Доказательство:

Пусть Х1 любое допустимое решение исходной задачи I. Тогда на основании основного неравенства: F(X) ≤ Z(Y) или

≤

получим F(X1) ≤ Z(Y*). Однако Х1 - произвольное решение задачи I. Аналогично доказывается, что решение У* оптимально для задачи II

Теорема (критерий оптимальности Канторовича).

Если для некоторых допустимых планов и пары двойственных задач выполняется неравенство , то и являются оптимальными планами соответствующих задач.

Теорема (малая теорема двойственности).

Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них.

9. Экономический смысл оптимальных переменных пары двойственных задач.

Рассмотрим исходную и двойственную задачу:

I. max f(x)=c₁x₁+c₂x₂ II. min g(y)=b₁y₁+b₂y₂

a₁₁x₁+a₁₂x₂≤b₁ y₁≥0

a₂₁x₁+a₂₂x₂≤b₂ y₂≥0

x₁>0 a₁₁y₁+a₂₁y₂≥c₁

x₂>0 a₁₂y₁+a₂₂y₂≥c₂

Если исходная и двойственная задачи имеют планы, то они имеют и оптимальные планы и функции цели на оптимальных планах равны

f(x⁻*)=c₁x₁*+c₂x₂*=g(y⁻*)=b₁y₁*+b₂y₂*

Е

В

Y2

сли задача содержит 2 переменные, то она допускает графическое решение

C2

C1

y1

b₁’y₁+b₂’y₂=c₂

b₁y₁+b₂y₂=c₁

Рассмотрим g(y*)=b₁y₁*+b₂y₂*

Коэффициенты b₁ И b₂ допускают изменения при которых значения функции целей не меняется

Рассмотрим функцию зависящую от b₁ и b₂

F(b₁, b₂)=b₁y₁*+b₂y₂*; b₁, b₁+∆b₁

Тогда функция так же получит приращение

F(b₁+∆b₁, b₂)=(b₁+∆b₁)y₁*+b₂y₂*

Приращение функции

∆F(b₁,b₂)=F(b₁+∆b, b₂) – F(b₁, b₂)=∆b₁y₁*, разделим левую и правую части на ∆b₁ и перейдем к пределу

Lim (∆F(b₁,b₂))/∆b1= lim (∆b₁y₁*)/∆b₁=y₁*

(∆b₁→0) (∆b₁→0)

(∂F(b₁, b₂))/∂b₁=y₁*

(∂F(b₁, b₂))/∂b₂=y₂*

Из последних равенств следует что переменные двойственные задачи показывают скорость изменения стоимости в зависимости от запасов ресурсов

y₁*, y₂* - называют «теневые цены»

10. Транспортная задача. Существование оптимального плана. Построение начального базисного плана способом наименьшей стоимости.

Транспортная задача — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.

Критерии оптимальности. Каждому базисному распределению поставок соответствует разбиение переменных задачи на свободные(они соответствуют свободным клеткам и только им) и базисным. Коэффициент β_ij ­при свободной переменной x_ij в выражении целевой функции F через свободные переменные называется оценкой свободной клетки (I, j). Транспортная задача- задача на минимум. Тогда из критерия оптимальности симплексного метода следует критерий оптимальности транспортной задачи: базисное распределение поставок оптимально только тогда, когда оценки всех свободных клеток неотрицательны.

Требуется определить опорный план и путём последовательных операций найти оптимальное решение. Опорный план можно найти следующими методами: «северо-западного угла»,«наименьшего элемента», 

Метод наименьшего элемента

Одним из способов решения задачи является метод минимального (наименьшего) элемента. Его суть заключается в сведении к минимуму побочных перераспределений товаров между потребителями.

Алгоритм:

1. Из таблицы стоимостей выбирают наименьшую стоимость и в клетку, которая ей соответствует, вписывают большее из чисел.

2. Проверяются строки поставщиков на наличии строки с израсходованными запасами и столбцы потребителей на наличие столбца, потребности которого полностью удовлетворены. Такие столбцы и строки далее не рассматриваются.

3. Если не все потребители удовлетворены и не все поставщики израсходовали товары, возврат к п. 1, в противном случае задача решена.