15. Признаки Дирихле и Абеля сходимости несобственных интегралов.

Теорема 1( признак Абеля): Пусть выполнены следующие условия:

1. сходится.

2. монотонна и ограничена на [a,b) M | ≤ M [a,b).

Если выполняются эти условия, то сходится.

Теорема 2 (признак Дирихле): Пусть выполнены следующие условия:

1. первообразная F = ограничена на [a,b), т.е. С: | | ≤ С [a,b).

2.функция монотонна на [a,b) и =0 ⇒ сходится.

Доказывается с использованием теоремы о среднем (формула Бонне) и критерия Коши о сходимости несобственных интегралов.

16. Абсолютная и условная сходимость несобственных интегралов (определение, теорема).

Определение: несобственный интеграл называется:

1.обсолютно-сходящийся, если сходится .

2.условно-сходящийся, если сам сходится , а - расходится.

Теорема: Из абсолютной сходимости вытекает обычная сходимость, т.е. сходится, причем выполняется неравенство ≤ .

Доказательство: 1) Если сходится, то сходится. Возьмем интеграл [a,b), тогда для определенного интеграла , справедливо неравенство ≤ . Т.к. сходится ⇒по теореме Коши сходится несобственный интеграл: >0 [a,b) [, b) ⇒ < ⇒по неравенству < ⇒по критерию Коши сходится. 2) Докажем неравенство. По свойству определенного интеграла для , [a,b), ≤ , сходится по теореме и сходится по пункту 1 ⇒ конечные пределы при 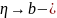. По свойству пределов неравенство сохраняет |≤ .

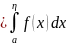Полезное утверждение для исследования сходимости интегралов

Теорема:1) Если конечен, т.е. -абсолютная интеграла на [a,b), тогда несобственный и либо оба сходятся абсолютно, либо сходятся условно, либо расходятся. 2) Прибавление (вычитание) под интегрируемой функции, не влияет не на сходимость интеграла, ни на характер этой сходимости (абсолютной, условной).

17. Метрическое пространство (определение, сходящиеся и фундаментальные последовательности, полное пространство, открытые и замкнутые множества, компакт, пространство ).

Определение: совокупность упорядоченных n-чисел , , … , где x R с обычными операциями покоординатного (покомпонентного) сложения и умножения на число называется n-мерным координатным пространством.

1) x+y= + + 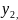… + ); 2) x= , … 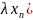; n-мерным коорд. пространством ( )

, , … ) , числа называются координатами точки .

Расстоянием между двумя точками , y называется число ς (x; y), d''(x; y)= .

Если заданно расстояние между двумя точками пространства , то говоря, что задана метрика в этом пространстве. Координатное пространство с введенной выше метрикой называют Евклидовым.

Окрестностью точки a (обозначим U (a)) называется множество точек x , таких, что (x, a)<

Точка a называется внутренней точкой множества M ⊂ , если U (a) ⊂M.

Точка a называется граничной точкой множества M, если в любой ее окрестности есть точки M и ∉ M.

Определение: множество M называют открытым, если все его точки внутренние. Множество называют замкнутым, если оно содержит все свои граничные точки.

Определение: замыканием множества M (обозначаем ) называется присоединение к множеству M всех его граничных точек. Замыкание множества называют замкнутым множеством.

Предельные точки

Утверждение: если множество x Евклидову пространству открыто, то -x замкнуто. Множество X лежащее в называют связанным, если для любых двух точек X существует непр. кривая, соединяющая эти точки, целиком лежащая в X.

Определение: областью называют: 1)открытое. 2)связанное множество.

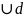Определение: замыкание области называют замкнутой областью в : = x X.

Определение (более общее определение окрестности): окрестностью точки можно называть открытое и связное множество содержащее точку (не обязательно шар).

Последовательности точек в

Определение: если любому натуральному К, поставлена в соответствие точка Xк ; Xк=( Xк1, Xк2,… Xкn). Говорят, что задана последовательность {Xк} в . Говорят, что Xк сходится к точке a (пишут Xк=a), если для 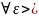0 N=N(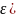 , что для К N⇒ (Xк, a)< (Xк, a)= .

Лемма 1: Если {Xк} имеет предел, то она ограничена.

Лемма 2: Если {Xк} имеет предел, то он единственный.

Лемма 3: Для того, чтобы {Xк} сходилась к a, необходимо и достаточно, чтобы выполнялась покоординатная сходимость. Xк→ a i (i=1, ) при Xк=a, a=(a1, …an) и Xкi ai.

Определение: последовательность {Xк} называется фундаментальной, если 0 N=N( , к, m N⇒ (Xк, Xm)<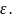

Утверждение (критерий Коши в ): последовательность {Xк} сходится в , когда последовательность фундаментальна.

Теорема (Больцано-Вейерштрасса): из любой ограниченной последовательности в можно выделить сходящуюся последовательность.

Компакт в

Определение: Множество M называют компактом, если из любой последовательности точек {Xк} M можно выделить сходящуюся подпоследовательность, причем lim этой подпоследовательности является точкой, лежащей в множестве M.

Теорема: Множество M компакт существует, когда выполняются 2 условия: 1)ограничена. 2)замкнута.