7.5. Понятие транслятора

Транслятор - программа или устройство, переводящее входную строку а языка А во выходную строку b языка B с сохранением смысла.

Это нестрогое определение, поскольку «сохранение смысла» можно понимать весьма различно.

аА bB

Т

Для того, чтобы облегчить переход от входного языка к выходному, а также с целью упростить оптимизацию, процесс трансляции часто разбивают на этапы, с трансляцией на промежуточные языки. Такие трансляторы называются многопроходными.

а = a₀ а₁ а₂ а₃ а_n = b

T₁ T₂ T₃ . . . T_n

По типу трансляции трансляторы подразделяются на компиляторы и интерпретаторы.

Компиляторы осуществляет перевод всего текста до начала выполнения (вычисления).

Интерпретатор транслирует исходный текст порциями. Он позволяет получать первые результаты уже на самых первых шагах обработки.

Интерпретатор обычно проще компилятора с аналогичного языка раз 10 – 100, но

примерно во столько же раз дольше идет обработка и требуются большие машинные ресурсы на этапе выполнения.

Компилятор и интерпретатор дополняют друг друга и каждый хорош на своем месте.

Самыми широко известными примерами интерпретаторов, кроме интерпретаторов Бейсика, служат операционные системы. Особенно это наглядно и многообразно представлено в ОС UNIX.

По уровню транслируемого языка интерпретаторы подразделяются на собственно интерпретаторы и ассемблеры.

Ассемблеры – это машинно-зависимые языки (низкого уровня). Исходный текст ассемблера, а более строго – макроассемблера - состоит из команд и макрокоманд. Макрокомандам соответствуют настраиваемые заготовки на языке ассемблера - макроописания, которые после необходимых настроек вставляются в текст программы.

Главная особенность макроассемблеров – это преобразование программного текста (текстовая замена) до начала трансляции – претрансляция. Эту функцию выполняет препроцессор.

Ассемблеры позволяют использовать преимущества и особенности конкретной архитектуры. С другой стороны ассемблеры привязаны к архитектуре.

7.6. Основные функции компилятора. Лексический анализ

1. Лексический анализ - приведение к некоторому стандартному виду ;

2. Синтаксический анализ - грамматический разбор ;

3. Семантический анализ - смысловой анализ;

4. Генерация выходного текста.

Лексический анализ выявляет лексемы - словарные единицы.

Основные функции лексического анализа:

1. выделение служебных слов языка (begin, while, for, …);

2. обработка численных констант;

3. выделение идентификаторов;

4. выделение сложных символов ( := <=);

5. внесение исправлений;

6. устранение различий устройств ввода;

7. устранение особенностей использования алфавитов, кодов.

7.7. Переход от недетерминированного распознающего автомата к детерминированному

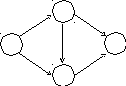
Состояния автомата и совокупности состояний, в который автомат переходит, объявляются множествами. Каждое из этих множеств становится состоянием нового детерминированного автомата. Переход из состояния, содержащего множество элементов, будет в состояние-множесто, составленное из всех состояний, в которые в исходном автомате осуществлялись переходы. Заметим, что пустые клеточки дают состояние - пустое множество.

	A	B	C	F
a	B,C		F
b	B	C,F

A  aB | bB | aC

B  bC | b

C  a

	{A}	{B,C}	{B}	{F}	{CF}	{}
a	{B,C}	{F}	{}	{}	{F}	{}
b	{B}	{C,F}	{C,F}	{}	{}	{}

B

a,b b

A b F

a a

C