4.12. Клика

Клика - максимально большой полный подграф данного графа.

a

f b

e c

d

	a	b	c	d	e	f
a		1	1
b				1	1	1
c					1	1
d					1	1
e						1
f

	a	b	c	d	e	f
a				1	1	1
b			1
c				1
d
e
f

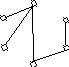
Построение Клики.

1. Строим дополнительный граф исходного графа.

G a

f b

e c

d

2. Найдем множество внутренней устойчивости для графа G.

(a  d)(a  e)(a  f)(b  c)(c  d)

(a  de)(a  f)(c  bd)

(a  def)(c bd)

ac  cdef  bdef  abd

{b, d, e, f}, {c, e, f}, {a, b}, {a, c}

3. Множества полученных вершин дают всевозможные полные подграфы исходного графа G. Причем, максимальный из подграфов дает клику.

5. Теория групп

Теория групп лежит в основе современной алгебры. Начала ее были созданы молодым гениальным математиком Э. Галуа (1811-1832) как инструмент для оценки возможности решения уравнений высших степеней в радикалах. Однако сфера применения и область интерпретации теории групп с тех пор многократно расширилась. Одна из самых значителных интерпретаций для групп – это различные типы симметрии.

5.1. Понятие группы

Группу можно задать как алгебру с одной операцией , удовлетворяющей следующим законам:

1. Существование операции.

xyz(x  y = z)

2. Ассоциативность

xyz(x  (y  z)) = ((x  y)  z)

3. Существование единицы (е)

еy(е  y = y)

4. Существование обратного элемента.

x!y(x  y = е)

5. Коммутативность

xy (x  y = y  x)

Выполнение лишь первого закона дает группоид. Если дополнительно выполняется второй – полугруппа (популярна при исследовании свойств формальных грамматик).

Выполнение первого, второго и третьего законов дает моноид.

Выполнение аксиом с первой по четвертую дает группу.

Если для группы выполняется также коммутативный закон, то группа называется абелевой.

5.2. Морфизмы групп

Рассмотрим вращения квадрата вокруг центра до совмещения вершин.

43

a₁ = 0⁰ В качестве элементов – углы поворота.

a₂ = 90⁰ В качестве операции - доворачивание.

a₃ = 180⁰ Выполняются все законы для группы.

a₄ = 270⁰

1 2

Например, а₁  а₂ = а₂; а₂  а₂ = а₃; а₃  а₃ = а₁

Популярны со времен Галуа и так называемые подстановки. Можно записать подстановки, соответствующие каждому из четырех вращений предыдущего примера:

1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4

       

1 2 3 4 4 1 2 3 3 4 1 2 2 3 4 1

А в качестве операции взять композицию подстановок. Например,

=

1 2 3 4 1 2 3 4 1 2 3 4

     

2 3 4 1 2 3 4 1 3 4 1 2

В результате также получится группа.

Возьмем корни уравнения x⁴ – 1 = 0

{1, i, -1, -i} - группа по операции умножения.

Таким образом, мы рассмотрели несколько конечных групп, содержащих по четыре элемента. Эти группы изоморфны между собой.

Например, можно отобразить друг в друга «единичные» элементы:

1 2 3 4

а₁  0⁰     1

1 2 3 4

Так что речь может идти об абстрактных группах, то есть о таких группах, для которых конкретное множество и конкретная операция несущественны.

Пусть f - некоторое отображение элементов одной группы в другую или в ту же самую и

f (a  b) = f(a)  f(b) a,b  G; f(a), f(b)  b₂.

то говорят, что f - гомоморфизм.

Если f(a)=F(b), тогда и только тогда, когда a = b, то имеем изоморфизм (однозначный гомоморфизм).

Гомоморфизм группы в себя называется эндоморфизмом.

Инъективный гомоморфизм называется мономорфизмом.

Сюръективный гомоморфизм называется эпиморфизмом.

Изоморфизм в себя называется автоморфизмом.

Пример : { . . .-3, -2, -1, 0, 1, 2, 3, . . . }

{ . . .-6, -4, -2, 0, 2, 4, 6, . . . } - эндоморфизм, эпиморфизм, мономорфизм, изоморфизм, автоморфизм.