
- •1. Общие сведения.
- •1.1. Основные понятия и определения.
- •1.2. Переменные в управлениях осу
- •1.3. Управление объектом
- •1.4. Классификация оптимальных систем управления.
- •2. Математическое описание
- •2.1. Уравнения в переменных состояния.
- •2.2. Представление нормальной системы уравнений в матричной форме.
- •2.3. Характеристическое уравнение в матричной форме.
- •2.4. Матричная передаточная функция.
- •2.5. Решение неоднородного матричного уравнения.
- •2.6. Метод фазовой плоскости
- •2.6.1. Особенности нелинейных систем
- •2.6.2. Изображение процессов на фазовой плоскости.
- •2.7. Фазовые портреты линейной системы
- •2.8. Фазовые портреты нелинейной системы.
- •2.9. Пример определения особых точек фазового портрета нелинейной системы.
- •2.10. Управление в фазовом пространстве.
- •Свободное движение.
- •Состояние равновесия.
- •Фазовый портрет при положительном управлении.
- •Фазовый портрет при отрицательном управлении.
- •Изменение движения изображающей точки.
- •3. Оптимальные системы.
- •3.1. Статическая оптимизация
- •Безусловная оптимизация
- •Условная оптимизация.
- •3.2. Динамическая оптимизация.
- •3.3. Функционал и его вариация.
- •3.4. Уравнение Эйлера.
- •3.5. Задачи вариационного исчисления
- •3.6. Принцип максимума.
- •3.7. Оптимальное по быстродействию управление на принципе максимума.
- •4. Адаптивные системы
- •4.1. Основные принципы
- •4.2. Постановка задачи.
- •3.2. Способы поиска экстремума.
- •4.3. Способы поиска экстремума.
2.6. Метод фазовой плоскости
2.6.1. Особенности нелинейных систем
Оптимальные системы автоматического управления – нелинейные. При этом они могут быть нелинейными по разному. Если нелинейная зависимость допускает линеаризацию разложением в ряд Тейлора, то она называется несущественной. В противном случае нелинейность существенная.
Примером существенной нелинейности являются статические характеристики релейных элементов. Вот некоторые: идеальное реле (рис. 2.1), реле с зоной нечувствительности (рис. 2.2), реле с гистерезисом (рис. 2.3), реле с зоной нечувствительности и гистерезисом (рис. 2.4).


На всех рисунках выходная величина y является разрывной функцией от входной величины x.
По сравнению с линейными, нелинейные системы обладают рядом особенностей.
1. Нелинейная система может иметь несколько положений равновесия. Что обнаруживается в реальных объектах. Линейные уравнения позволяют рассчитать только одно состояние равновесия.
2. Решение линейного уравнения даёт формулу, по которой переходной процесс завершается через бесконечно – большое время. В природе и технике такого нет. За счет нелинейности, реальные системы завершают процессы в конечное время.
3. Если линейная система неустойчива, значения выходных переменных неограниченно растут. В нелинейной системе рост переменных ограничивается.
4. Нелинейная система может совершать периодические движения без приложения внешней силы – автоколебания. В линейной системе автоколебания принципиально невозможны. То есть линейная теория не предсказывает такого явления.
5. В линейной системе выполняется принцип суперпозиции: при сложении воздействий реакция равна сумме реакций на отдельные воздействия. Нелинейные системы этого не допускают: реакции получаются разные.
6. Устойчивость и характер переходного процесса в нелинейной системе зависит от величины входного воздействия. Линейной системе безразлично, какой величины будет входное воздействие.
2.6.2. Изображение процессов на фазовой плоскости.
Одним из наиболее эффективных и наглядных методов качественного исследования нелинейных систем является построение фазовых портретов.
Если уравнения системы автоматического управления представлены в нормальной форме, то вектор состояния системы однозначно определяет её состояние. В пространстве состояний каждому состоянию системы соответствует точка. Точка, соответствующая текущему состоянию называется изображающей точкой. При изменении состояния изображающая точка описывает траекторию, которая называется фазовой траекторией. Совокупность фазовых траекторий, каждая для своих начальных условий, называется фазовым портретом.
В случае многомерной системы фазовая траектория образуется в многомерном фазовом пространстве.
Наглядно фазовую траекторию можно изобразить на плоскости.
Фазовая плоскость имеет две координаты. По абсциссе откладывают фазовую переменную, по ординате – её производную, фазовую скорость. Эти координаты однозначно определяют состояние системы второго порядка.
Метод анализа и синтеза системы автоматического управления, основанный на построении фазового портрета, называется методом фазовой плоскости.
Фазовые траектории на плоскости служат для анализа дифференциального уравнения второго порядка вида:
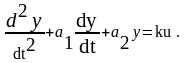
Дифференциальное уравнение второго порядка преобразуется в систему уравнений состояния второго порядка. В общем виде она имеет вид:
 ,
,
(2.18)

Функции
 и
и
 в общем случае нелинейные.
в общем случае нелинейные.
Разделим
второе уравнение на первое (имея ввиду,
что
 ):
):
 .
(2.19)
.
(2.19)
Получили общего вида дифференциальное уравнение фазовых траекторий. Оно непосредственно связывает фазовые координаты. Проанализируем это уравнение.
Если
одновременно
 и
и
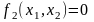 , то
, то
 , (2.20)
, (2.20)
Уравнение
(2.20) определяет особые точки фазового
портрета. В особых точках фазовая
скорость

это следует из уравнения (4.1). Значит,
особые
точки являются положениями равновесия.
Через каждую точку на плоскости проходит
только одна траектория – через особую
точку может проходить много траекторий.
это следует из уравнения (4.1). Значит,
особые
точки являются положениями равновесия.
Через каждую точку на плоскости проходит
только одна траектория – через особую
точку может проходить много траекторий.
Когда состояние системы изменяется, изображающая точка движется по некоторой траектории. Выясним, в каком направлении движется изображающая точка.
Рассмотрим
траекторию на рис 2.5. В верхней
полуплоскости, Значит, координата
Значит, координата
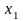 возрастает. Изображающая точка
движется слева направо. В нижней
полуплоскости изображающая точка
движется справа налево, так как
возрастает. Изображающая точка
движется слева направо. В нижней
полуплоскости изображающая точка
движется справа налево, так как
 ,
уменьшается. На оси абсцисс
,
уменьшается. На оси абсцисс
 ,
из уравнения 2.19 следует, что
,
из уравнения 2.19 следует, что .
Значит, фазовые траектории пересекают
ось абсцисс под прямым углом.
.
Значит, фазовые траектории пересекают
ось абсцисс под прямым углом.

По
виду траектории можно судить об
устойчивости системы. Траектория
начинается в момент времени t
= 0, когда изображающая точка М имеет
начальные координаты,
 . В этот момент система начала переход
из одного состояния в другое. Если
переходной процесс завершается
установившемся состоянием, на фазовой
плоскости изображающая точка М
. В этот момент система начала переход
из одного состояния в другое. Если
переходной процесс завершается
установившемся состоянием, на фазовой
плоскости изображающая точка М
 из любого положения переместится в
начало координат т.е., траектория
закончится в начале координат.
Траектория, заканчивающееся в начале
координат, свидетельствует об устойчивой
системе, рис 2.6. Если изображающая
точка неограниченно удаляется от начала
координат, это свидетельствует о
неустойчивой системе, рис 2.7.
из любого положения переместится в
начало координат т.е., траектория
закончится в начале координат.
Траектория, заканчивающееся в начале
координат, свидетельствует об устойчивой
системе, рис 2.6. Если изображающая
точка неограниченно удаляется от начала
координат, это свидетельствует о
неустойчивой системе, рис 2.7.

В случае устойчивой системы фазовые траектории как бы притягиваются особой точкой – началом координат. Такая особая точка получила название “центр притяжения”. В случае неустойчивой системы особая точка как бы отталкивает фазовую траекторию, т.е. это будет центр отталкивания.
Для линейных систем существует только один центр притяжения или отталкивания – начало координат. Нелинейные системы могут иметь несколько таких центров.
Пример 4.1. Линеаризовать систему (2.18.)


в
точке ,
, .
.
Для этого надо разложить правые части в ряд Тейлора:


 ,
т.к.
,
т.к.
 (начало
координат). Частные производные в
фиксированных точках есть коэффициенты:
(начало
координат). Частные производные в
фиксированных точках есть коэффициенты:


Система линейных уравнений состояния получает вид:


