Условная оптимизация.

Если переменные, входящие в целевую функцию изменяются взаимосвязано, то для оптимизации необходимо указать связи между ними. То есть, должна быть еще одна функция. В поставке задачи будет целевая функция

(3.8)

и функция связи (или уравнение связи)

. (3.9)

Требуется среди переменных найти такие, которые делают экстремальным критерий Q в пределах, которые дозволяет функция F.

Такая задача называется условной оптимизацией.

Задачи условной оптимизации решают методом неопределённых множителей Лагранжа. Метод состоит в следующем. К имеющимся переменным добавляют еще одну, λ и записывают функцию Лагранжа, общий вид которой

(3.10)

Необходимые условия экстремума – обращение в нуль частных производных функции Лагранжа:

(3.11)

Эта система уравнений позволяет найти переменные экстремума.

Таким образом, поиск условного экстремума осуществляется не с функцией цели, а с составленной по определённому правилу функцией Лагранжа.

Рассмотрим пример. Требуется изготовить из листовой стали прямоугольную открытую ёмкость заданного объема V. Надо выбрать такие размеры, чтобы расход металла был минимальным.

Пусть a, b – стороны, h – высота бака, рис. 3.3. Понадобятся листы стали общей площадью . Площадь надо сделать минимальной. То есть, функцией цели будет площадь листов стали . Однако, переменные должны меняться при условии, что объём V сохраняется постоянным, он задан. Значит, есть уравнение связи, ограничивающее изменение переменных. Или, по-другому, условие, которое накладывается на изменение переменных.

Это задача на условный экстремум.

Введём вспомогательную переменную λ и выпишем функцию Лагранжа:

Возьмём частные производные и приравняем их нулю:

, (α)

, (β)

, (δ)

, (γ)

Из уравнения (α) и уравнения (β) следует, что экстремальные переменные b^* и a^* имеют одинаковый вид:

, .

то есть, b^* = a^*.

Из уравнения (δ) получается . Заменим λ в уравнении (β) и получим: . По заданному объёму находится оптимальная сторона :

Заключаем: бак должен иметь в основании квадрат и высоту вдвое меньше стороны.

3.2. Динамическая оптимизация.

В задачах статической оптимизации критерием оптимизации является функция одной или нескольких переменных: функция цели.

В задачах динамической оптимизации и оптимального управления критерием оптимальности является функционал.

3.3. Функционал и его вариация.

Функционал – это функция от функции.

Понятие функционала отличается от понятия функции. Функцией называется закон, по которому одна величина зависит от другой. Например, y = x², y = x³, y = sin x, в общем виде y = f (x). Каждому значению x отвечает некоторое значение y. Пусть y = x². Тогда при x = 2 получим y = 4, при x = 0,25 получим y = 0,625, и т.д. То есть функция y = f (x) есть закон, согласно которому числам x отвечают числа y.

Рассмотрим формулу:

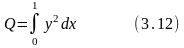
Если вместо y подставить различные конкретные функции, то будут получаться конкретные числовые значения Q. Например, выбрав y = x², получим

Выбрав y = x³, получим Q = 0,143. Для y = sin x, получим 0,3.

Таким образом, формула (3.12.) задаёт закон, согласно которому каждой функции y(x) соответствует число. Такой закон называется функционалом.

Формула определяет другой функционал. Формула - третий. Набору функций будут соответствовать числа Q₁ , Q₂ , …

Итак, если числам ставятся в соответствие числа – задана функция. Если функциям ставятся в соответствие числа – задан функционал.

Возможен функционал от нескольких функций.

Более общим является закон преобразования, когда каждой функции f(x) соответствует новая функция F. Иными словами, каждая функция f(x) по какому-то определённому закону преобразуется в новую функцию F. Такой закон преобразования функций в функцию в математике называется оператором. Примером является оператор дифференцирования d, воздействующий по закону df = f`: d(sin x) = cos x , d(x²) = 2x .

Более сложный случай – оператор Лапласа, преобразующий функцию действительного переменного в функцию комплексного переменного:

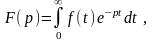
где , t – время.

Задача динамической оптимизации математически означает поиск максимума или минимума функции от функции.

Чтобы найти экстремум функционала, приравнивают нулю вариацию функционала: Q = 0 .

Вариация функционала определяется через вариацию функции. Вариацией функции y(x) и близкой к ней функции 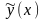называется их разность

Близость означает, что отличается на небольшую величину от y(x). Близость нулевого порядка означает близость функции по модулю:

где  - малая величина.

Если функции и y(x) имеют производные, то их разность будет вариацией производной:

Определим вариацию функционала.

Вариация функционала Q  это главная, линейная по отношению к вариации функции y(x) часть приращения:

Условие экстремума функционала в точке экстремума y^*(х) = y(х) есть

y^*  функция доставляющая экстремум функционалу.

В качестве примера получим вариацию функционала

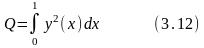
Допустим, сначала была функция y = y(x), а затем в функционал подставили другую функцию y(x) + y(x) , где y(x)  вариация y(x). Вариация y(x)  некая произвольная функция, принимающая малые значения. (Например, могло быть сначала y = x² , а затем y = x² + x³ , где   малая величина). Значение функционала (3.12) немного изменится и станет равным:

Приращение функционала будет:

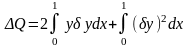
Ввиду малости, можно отбросить. Оставшийся член есть вариация функционала

Запишем теперь функционал общего вида:

Дадим приращение и выполним разложение по формуле Тейлора:

Линейная часть приращения есть вариация функционала

Полагая F = y²(х) и применяя общую формулу (3.15) к функционалу (3.12) получаем (3.13).

Для функционала другого вида получается другая вариация Q.

Пусть функция у(х) реализует экстремум функционала. То есть, значение функционала для у(х) больше (в случае max) или меньше (в случае min) значения этого функционала для всех функций, достаточно близких к у(х). Тогда условием экстремума будет Q = 0.Или, имея ввиду (3.15),

Функция, на которой вариация функционала равна нулю, называется «экстремаль».