3.6. Принцип максимума.

Так называется математический метод, который считается эффективным для решения задач оптимального управления.

Задача оптимального управления сводится к отысканию таких управляющих величин u_i , которые, одновременно с переводом объекта управления из одного состояния в другое, обеспечивают экстремум критерия оптимальности.

Рассмотрим управление автономной системой на принципе максимума.

Система называется автономной, если правые части дифференциальных уравнений, описывающих ее движение, явно не зависят от времени:

Функция критерия оптимальности автономной системы не содержит время,

называется основной:

Для решения вводится вспомогательная переменная (t) и записывается система уравнений для переменных по правилу:

Эта система дифференциальных уравнений называется сопряженной основной системе дифференциальных уравнений.

В теории вариационного исчисления доказывается, что системы (3.27) и (3.28) можно объединить в одну, если ввести в рассмотрение функцию Гамильтона:

Заменяя производные в соответствии с (3.27), получим:

С помощью гамильтониана основную и сопряженную системы представляют в форме канонических уравнений:

Переменная u(t)  является управлением, переводящим изображающую точку из начального положения x(t₀) в конечное х(Т). По траектории x(t).   вектор-функция, она определяет направление вектора скорости движения изображающей точки в п-мерном фазовом пространстве.

Изменяя определенным образом вектор-функцию  , можно обеспечить максимальное значение гамильтониана. При максимуме гамильтониана управление будет оптимальным. То есть, управление оптимально, если обеспечить

Выражение (3.33) есть принцип максимума. Принцип максимума устанавливает связь между управлением u(t) и координатами основной и сопряженной систем. Управление должно быть таким, чтобы H был максимальным в каждой точке траектории. В таком случае траектория изображающей точки становится оптимальной.

Порядок решения задач с помощью принципа максимума следующий.

1. Записать основную систему уравнений объекта в переменных состояния совместно с уравнением критерия оптимальности:

2. Составить функцию Гамильтона:

3. Составить канонические уравнения для определения :

4. Определить значения вектор-функции u , максимизирующей функцию Гамильтона:

Искомое оптимальное управление выражается через функции .

3.7. Оптимальное по быстродействию управление на принципе максимума.

Дано уравнение объекта

На управляющую величину наложено ограничение

- 1 ≤ u ≤ + 1 .

Требуется найти условия оптимальности управления.

1. Записываем дифференциальное уравнение в переменных состояниях

Начальные условия: t = 0,

2. Задаем быстродействие критерием оптимальности

Примем простоты ради  = 1 .

3. Придадим критерию оптимальности смысл дополнительной переменной состояния и обозначим через . Продифференцировав (3.35), получаем уравнение:

_{4. Записываем основную систему дифференциальных уравн}ений в переменных состояниях:

5. Составим гамильтониан системы уравнений (3.36):

 вспомогательные функции, которые необходимо определить в дальнейшем.

6. Потребуем оптимальность управления. Оптимальным управление будет тогда, когда выполняется требование максимума гамильтониана: . Их всех трех слагаемых только последнее слагаемое зависит от управления u . Значит, гамильтониан будет максимальным при максимальном значении последнего слагаемого: .

Величина u экстремальна на границах ограничения: u = + 1 или u =  1 .

Произведение u максимально либо когда  > 0 , u = + 1, либо когда  < 0 , u =  1. То есть, знак функции должен быть такой же, какой знак имеет u . В таком случае, знак управления можно определять по знаку :

7. Записать систему канонических уравнений (3.26) чтобы определить вид функции :

,

,

.

Решениями уравнений будут функции

8. Находим закон управления. Подставляя ψ₂ в выражение (3.37), получаем:

Полученное выражение показывает, какому требованию должно удовлетворять оптимальное управление. Функция С₂ – С₁ t  – линейная, может менять знак не более одного раза. Следовательно, оптимальное управление представляет собой кусочно-постоянную функцию, которая принимает предельные значения + 1 или – 1, и имеет два интервала постоянства. Момент переключения определяется сменой знака функции (С₂ – С₁ t) .

В промежутке времени 0 ≤ t ≤ t₁ надо осуществлять воздействие u = 1, в промежутке от t₁ до Т – воздействие u =  1.

9. Определение фазовых траекторий.

Характер движения системы изображается фазовым портретом. Получим фазовые траектории.

, ,

Для положительного управления u = + 1 связь между и :

(3.39)

Фазовые траектории – семейство парабол, рис. 6.2.

Рис. 6.2. Фазовые траектории

при положительном управлении.

Для отрицательного управления

. (3.40)

Фазовые траектории показаны на рис. 6.3.

Рис. 6.3. Фазовые траектории при отрицательном управлении.

10. Построение фазового портрета управления.

На фазовой плоскости начальное состояние системы изображается точкой М(x₁,x₂). Процесс управления отображается движением изображающей точки по одной из фазовых траекторий на рис. 6.2 или рис. 6.3. Когда управление завершается, система приходит в равновесие. Изображающая точка должна попасть на начало координат, где =0 , =0.

Через начало координат проходят только две параболы:

(u = + 1) , (3.41)

и

(u = - 1) . (3.42)

По какой бы фазовой траектории не двигалась изображающая точка М , на заключительном этапе движения она должна попасть на траекторию (3.41) или (3.42).

На графике рис. 6.4 изображены те ветви парабол (3.41) и (3.42), по которым изображающая точка попадает в начало координат: это АО и ВО . (Ветви ОА' и ОВ' во внимание не принимаются, т. к. по ним изображающая точка удаляется от начала координат). Ветвь АО отвечает условиям u = 1 , x₂ < 0 . Ветвь ВО – условиям u =  1 , x₂ > 0 .

Рис. 6.4. Траектории, по которым изображающая точка попадает в начало координат.

Используя знак x₂ , уравнения (6.28) и (6.29) можно записать одним:

(3.43)

Из начального положения изображающая точка движется при отрицательном или положительном управлении, пока не попадет на линию АО или ВО . На линии происходит переключение знака управления и изображающая точка попадает в начало координат, рис. 6.5 .

Рис. 6.5. Возможные траектории движения изображающей точки от начала и до конца управления.

Линию с уравнением (3.43) называют линией переключения.

По семейству парабол изображающая точка движется снизу – вверх, т. к. . По семейству парабол

изображающая точка движется сверху-вниз, т. к. dx₂ / dt =  1 < 0 . Чтобы управление завершилось, изображающая точка должна попасть в начало координат.

Для заданной изображающей точки М ( , 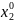) фазовая траектория состоит из «своей» параболы и отрезка параболы АО . На дуге АО управление переключается с u =  1 на u = + 1 и остается таким до прихода изображающей точки в начало координат, рис. 6.5 .

Задание изображающей точки однозначно определяет оптимальную траекторию.

Определение констант в формулах (3.39) и (3.40) по начальным условиям

При управлении u = + 1

Исключая время и полагая по формуле (3.39) получаем:

Тем же путем, для управления u =  1 , получаем