2. Математическое описание

2.1. Уравнения в переменных состояния.

В общем виде дифференциальное уравнение одномерного управляемого объекта имеет вид

где a_i , b – коэффициенты, u(t) – воздействие.

Разрешим уравнение (2.1) относительно старшей производной:

(2.2)

Введем новые переменные по правилу

.

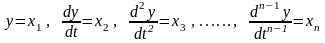и учтем, что . Преобразуем уравнение (2.2), получим систему:

……….. (2.3)

Переменные x₁ , x₂ , …, x_n называют «переменные состояния», «фазовые координаты» или «фазовые переменные». называют «уравнение выхода».

Если объект управления описывается несколькими дифференциальными уравнениями, преобразование к переменным состояния можно применить к каждому из них.

В общем случае получается система уравнений вида

…………………………………

вместе с уравнениями выхода

В векторном виде

(2.4)

Теперь в системе (2.4) х – вектор состояний или фазовый вектор, u – вектор управления, или просто «управление».

Каждому состоянию системы (заданы компоненты x_i вектора состояния) можно поставить в соответствие точку в n – мерном евклидовом пространстве, а движение динамической системы во времени отобразится n – мерной траекторией.

Уравнения, записанные в виде системы дифференциальных уравнений первого порядка, разрешенных относительно первой производной, называют уравнениями состояния, нормальной формой или канонической формой.

2.2. Представление нормальной системы уравнений в матричной форме.

Обратимся к записи (2.2). Дополним правую часть нулевыми членами:

…………...... (2.5)

Анализируя систему (2.5), можно сделать заключение, какой вид имеют матрицы входящих в нее величин:

.

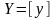Следовательно, матричной формой записи системы (2.5) будет

(2.6)

A – (nn)-матрица, B– (nm)-матрица.

X – матрица неизвестных переменных. u – известная функция времени.

Если в системе (2.6) что-то изменится, это приведет к изменению вида матриц. Общий вид уравнения (2.6) останется тем же.

Пример 2.1. Дана система

Записать в матричной форме.

Общая форма матричного уравнения

Матрицы находим по полной записи системы уравнений

Матрицы имеют вид:

.

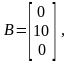
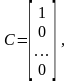2.3. Характеристическое уравнение в матричной форме.

Для линейных систем характеристическое уравнение получают преобразованием Лапласа уравнения (2.1).

Операторное уравнение имеет вид:

Полином D(p), приравненный нулю, есть характеристическое уравнение линейной системы: D(p) = 0 .Решение характеристического уравнения позволяет найти корни p_i и построить решение в виде суммы экспонент:

Это решение одномерной системы.

Многомерная система имеет математическую модель в матричной форме

(каноническая система n-го порядка)

Применяя к матричному уравнению преобразование Лапласа, для нулевых начальных условий получаем

или

где Е – единичная матрица, А – основная матрица.

Левая часть, приравненная нулю, дает уравнение свободного движения системы

.

0 – нуль-матрица.

По аналогии с операторным уравнением (2.7) заключаем, что характеристическое уравнение – это определитель левой матричной части, равный нулю:

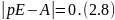
Корни p_i уравнения (2.8) называются собственными значениями или характеристическими числами основной матрицы  А.

Пример 2.1.

Найти характеристическое уравнение для матрицы

.

dim A = 22, следовательно единичную матрицу Е надо взять такого же размера. Следуя формуле (2.8), записываем:

.

Получается характеристическое уравнение , которое имеет корни .